算法3.爬楼梯与动态规划详解

        以前经常听别人说动态规划，贪心算法，暴力枚举，然后就感觉这些东西不应该属于自己学习的范围，听上去就很高深。今天碰到一篇文章，看完之后，发现上边的三个词汇一下子没有那么高深了，而且我自身感觉到这三个词汇放到我们生活中去指导我们做事情，也是非常有帮助的。为了防止文章失联，我先把文章放到算法集锦列表里面，让更多的新手小白可以看到，不用再去辛苦找对应的文章了，而且运气不好碰到天书，直接让人丧失自信可不太好。

先解答一道题目：

        假设你正在爬楼梯。需要n个台阶你才能到达楼顶。每次你可以爬1或者2个台阶。你有多少种不同的方法可以爬到楼顶呢？给定n是一个正整数。

---

直接来最简单的解法：

         我们用 f(x)表示爬到第 x 级台阶的方案数，考虑最后一步可能跨了一级台阶，也可能跨了两级台阶，所以我们可以列出如下式子：

f(x) = f(x - 1) + f(x - 2)

        它意味着爬到第 x 级台阶的方案数是爬到第 x−1 级台阶的方案数和爬到第 x - 2 级台阶的方案数的和。很好理解，因为每次只能爬 1 级或 2 级，所以 f(x) 只能从 f(x - 1) 和 f(x−2) 转移过来，而这里要统计方案总数，我们就需要对这两项的贡献求和。

        以上是动态规划的转移方程，下面我们来讨论边界条件。我们是从第 0 级开始爬的，所以从第 0 级爬到第 0 级我们可以看作只有一种方案，即 f(0) = 1；从第 0 级到第 1 级也只有一种方案，即爬一级，f(1) = 1。这两个作为边界条件就可以继续向后推导出第 n 级的正确结果。我们不妨写几项来验证一下，根据转移方程得到 f(2) = 2，f(3) = 3，f(4) = 5，……，我们把这些情况都枚举出来，发现计算的结果是正确的。

        我们不难通过转移方程和边界条件给出一个时间复杂度和空间复杂度都是 O(n) 的实现，但是由于这里的 f(x) 只和 f(x - 1) 与 f(x - 2) 有关，所以我们可以用「滚动数组思想」把空间复杂度优化成 O(1)。

下面的代码中给出的就是这种实现。

class Solution {    public int climbStairs(int n) {        int p = 0, q = 0, r = 1;        for (int i = 1; i <= n; ++i) {            p = q;             q = r;             r = p + q;        }        return r;    }}

        上边这个其实就是前几天写的斐波那契数列。忽然想起来自己曾经在美团用的就是这种方式做出来的。不过那个时候也不知道这些乱七八糟的概念，什么滚动数组，就是靠感觉推测出来的。

---

好了接下来让我们看看大佬对于动态规划，贪心算法，暴力枚举的解读吧。

　　很有意思的问题。以往见过许多教材，对动态规划（DP）的引入属于“奉天承运，皇帝诏曰”式：不给出一点引入，见面即拿出一大堆公式吓人；学生则死啃书本，然后突然顿悟。针对入门者的教材不应该是这样的。恰好我给入门者讲过四次DP入门，迭代出了一套比较靠谱的教学方法，所以今天跑过来献丑。

　　现在，我们试着自己来一步步“重新发明”DP。

1. 从一个生活问题谈起

　　先来看看生活中经常遇到的事吧——假设您是个土豪，身上带了足够的1、5、10、20、50、100元面值的钞票。现在您的目标是凑出某个金额w，需要用到尽量少的钞票。

　　依据生活经验，我们显然可以采取这样的策略：能用100的就尽量用100的，否则尽量用50的……依次类推。在这种策略下，666=6×100+1×50+1×10+1×5+1×1，共使用了10张钞票。

　　这种策略称为“贪心”：假设我们面对的局面是“需要凑出w”，贪心策略会尽快让w变得更小。能让w少100就尽量让它少100，这样我们接下来面对的局面就是凑出w-100。长期的生活经验表明，贪心策略是正确的。

　　但是，如果我们换一组钞票的面值，贪心策略就也许不成立了。如果一个奇葩国家的钞票面额分别是1、5、11，那么我们在凑出15的时候，贪心策略会出错：
　　15=1×11+4×1   （贪心策略使用了5张钞票）
　　15=3×5（正确的策略，只用3张钞票）
　　为什么会这样呢？贪心策略错在了哪里？

　　鼠目寸光。
　　刚刚已经说过，贪心策略的纲领是：“尽量使接下来面对的w更小”。这样，贪心策略在w=15的局面时，会优先使用11来把w降到4；但是在这个问题中，凑出4的代价是很高的，必须使用4×1。如果使用了5，w会降为10，虽然没有4那么小，但是凑出10只需要两张5元。
　　在这里我们发现，贪心是一种只考虑眼前情况的策略。

　　那么，现在我们怎样才能避免鼠目寸光呢？

　　如果直接暴力枚举凑出w的方案，明显复杂度过高。太多种方法可以凑出w了，枚举它们的时间是不可承受的。我们现在来尝试找一下性质。

　　重新分析刚刚的例子。w=15时，我们如果取11，接下来就面对w=4的情况；如果取5，则接下来面对w=10的情况。我们发现这些问题都有相同的形式：“给定w，凑出w所用的最少钞票是多少张？”接下来，我们用f(n)来表示“凑出n所需的最少钞票数量”。

　　那么，如果我们取了11，最后的代价（用掉的钞票总数）是多少呢？明显

cost = f(4)+1 = 4+1 = 5 

      它的意义是：利用11来凑出15，付出的代价等于f(4)加上自己这一张钞票。现在我们暂时不管f(4)怎么求出来。
　　依次类推，马上可以知道：如果我们用5来凑出15，cost就是

f(10) + 1 = 2+1 =3

　　那么，现在w=15的时候，我们该取那种钞票呢？当然是各种方案中，cost值最低的那一个！

　　- 取11：cost = f(4)+1 = 4+1 = 5
　　- 取5：  cost = f(10)+1 =  2+1 = 3 
　　- 取1： cost = f(14)+1 = 4+1 = 5

　　显而易见，cost值最低的是取5的方案。我们通过上面三个式子，做出了正确的决策！

　　这给了我们一个至关重要的启示f(n)只与f(n-1),f(n-5),f(n-11)相关；更确切地说：

f(n) = min{f(n-1),f(n-5),f(n-11)}+1

　　这个式子是非常激动人心的。我们要求出f(n)，只需要求出几个更小的f值；既然如此，我们从小到大把所有的f(i)求出来不就好了？注意一下边界情况即可。代码如下：

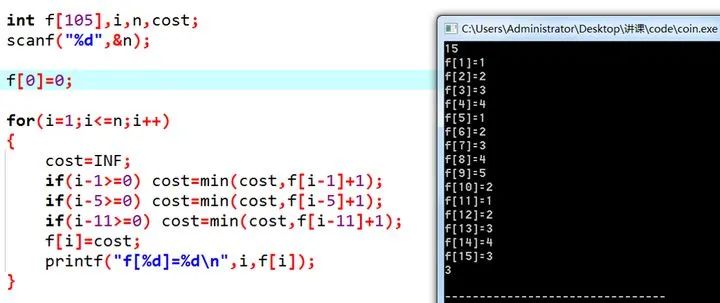
　　我们以 O(n) 的复杂度解决了这个问题。现在回过头来，我们看看它的原理：

　　- f(n) 只与f(n-1),f(n-5),f(n-11)的值相关。
　　- 我们只关心 f(w) 的值，不关心是怎么凑出w的。

　　这两个事实，保证了我们做法的正确性。它比起贪心策略，会分别算出取1、5、11的代价，从而做出一个正确决策，这样就避免掉了“鼠目寸光”！

　　它与暴力的区别在哪里？我们的暴力枚举了“使用的硬币”，然而这属于冗余信息。我们要的是答案，根本不关心这个答案是怎么凑出来的。譬如，要求出f(15)，只需要知道f(14),f(10),f(4)的值。其他信息并不需要。我们舍弃了冗余信息。我们只记录了对解决问题有帮助的信息——f(n).

　　我们能这样干，取决于问题的性质：求出f(n)，只需要知道几个更小的f(c)。我们将求解f(c)称作求解f(n)的“子问题”。

　　这就是DP（动态规划，dynamic programming）.

　　将一个问题拆成几个子问题，分别求解这些子问题，即可推断出大问题的解。

思考题：请稍微修改代码，输出我们凑出w的方案。

2. 几个简单的概念

【无后效性】

　　一旦f(n)确定，“我们如何凑出f(n)”就再也用不着了。

　　要求出f(15)，只需要知道f(14),f(10),f(4)的值，而f(14),f(10),f(4)是如何算出来的，对之后的问题没有影响。

　　“未来与过去无关”，这就是无后效性。

　　（严格定义：如果给定某一阶段的状态，则在这一阶段以后过程的发展不受这阶段以前各段状态的影响。）

【最优子结构】

　　回顾我们对f(n)的定义：我们记“凑出n所需的最少钞票数量”为f(n).

　　f(n)的定义就已经蕴含了“最优”。利用w=14,10,4的最优解，我们即可算出w=15的最优解。

　　大问题的最优解可以由小问题的最优解推出，这个性质叫做“最优子结构性质”。

　　引入这两个概念之后，我们如何判断一个问题能否使用DP解决呢？

　　能将大问题拆成几个小问题，且满足无后效性、最优子结构性质。

3. DP的典型应用：DAG最短路

　　问题很简单：给定一个城市的地图，所有的道路都是单行道，而且不会构成环。每条道路都有过路费，问您从S点到T点花费的最少费用。

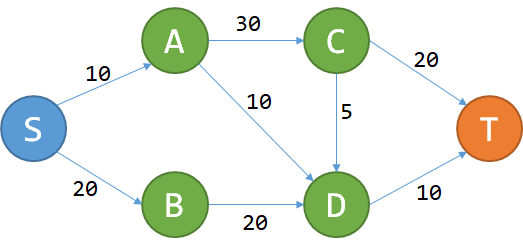一张地图。边上的数字表示过路费。

　　这个问题能用DP解决吗？我们先试着记从S到P的最少费用为f(P).
　　想要到T，要么经过C，要么经过D。从而

f(T) = min{f(C)+20,f(D)+10}

　　好像看起来可以DP。现在我们检验刚刚那两个性质：
　　- 无后效性：对于点P，一旦f(P)确定，以后就只关心f(P)的值，不关心怎么去的。
　　- 最优子结构：对于P，我们当然只关心到P的最小费用，即f(P)。如果我们从S走到T是 S-P-Q-T ，那肯定S走到Q的最优路径是 S-P-Q 。对一条最优的路径而言，从S走到沿途上所有的点（子问题）的最优路径，都是这条大路的一部分。这个问题的最优子结构性质是显然的。

　　既然这两个性质都满足，那么本题可以DP。式子明显为：

        f(P) = min{f(R)+Wr-p}

　　其中R为有路通到P的所有的点， Wr-p 为R到P的过路费。

　　代码实现也很简单，拓扑排序即可。

4. 对DP原理的一点讨论

【DP的核心思想】

　　DP为什么会快？
　　无论是DP还是暴力，我们的算法都是在可能解空间内，寻找最优解。

　　来看钞票问题。暴力做法是枚举所有的可能解，这是最大的可能解空间。
　　DP是枚举有希望成为答案的解。这个空间比暴力的小得多。

　　也就是说：DP自带剪枝。

　　DP舍弃了一大堆不可能成为最优解的答案。譬如：
　　15 = 5+5+5 被考虑了。
　　15 = 5+5+1+1+1+1+1 从来没有考虑过，因为这不可能成为最优解。

　　从而我们可以得到DP的核心思想：尽量缩小可能解空间。

　　在暴力算法中，可能解空间往往是指数级的大小；如果我们采用DP，那么有可能把解空间的大小降到多项式级。

　　一般来说，解空间越小，寻找解就越快。这样就完成了优化。

【DP的操作过程】

　　一言以蔽之：大事化小，小事化了。

　　将一个大问题转化成几个小问题；
　　求解小问题；
　　推出大问题的解。

【如何设计DP算法】

　　下面介绍比较通用的设计DP算法的步骤。

　　首先，把我们面对的局面表示为x。这一步称为设计状态。
　　对于状态x，记我们要求出的答案(e.g. 最小费用)为f(x).我们的目标是求出f(T).
找出f(x)与哪些局面有关（记为p），写出一个式子（称为状态转移方程），通过f(p)来推出f(x).

【DP三连】

　　设计DP算法，往往可以遵循DP三连：

　　我是谁？ ——设计状态，表示局面
　　我从哪里来？
　　我要到哪里去？ ——设计转移

　　设计状态是DP的基础。接下来的设计转移，有两种方式：一种是考虑我从哪里来（本文之前提到的两个例子，都是在考虑“我从哪里来”）；另一种是考虑我到哪里去，这常见于求出f(x)之后，更新能从x走到的一些解。这种DP也是不少的，我们以后会遇到。

　　总而言之，“我从哪里来”和“我要到哪里去”只需要考虑清楚其中一个，就能设计出状态转移方程，从而写代码求解问题。前者又称pull型的转移，后者又称push型的转移。

思考题：如何把钞票问题的代码改写成“我到哪里去”的形式？
提示：求出f(x)之后，更新f(x+1),f(x+5),f(x+11).