7-17 汉诺塔的非递归实现 (25分)

7-17 汉诺塔的非递归实现 (25分)

借助堆栈以非递归（循环）方式求解汉诺塔的问题（n, a, b, c），即将N个盘子从起始柱（标记为“a”）通过借助柱（标记为“b”）移动到目标柱（标记为“c”），并保证每个移动符合汉诺塔问题的要求。

输入格式:

输入为一个正整数N，即起始柱上的盘数。

输出格式:

每个操作（移动）占一行，按柱1 -> 柱2的格式输出。

输入样例:

3

输出样例:

a -> c
a -> b
c -> b
a -> c
b -> a
b -> c
a -> c

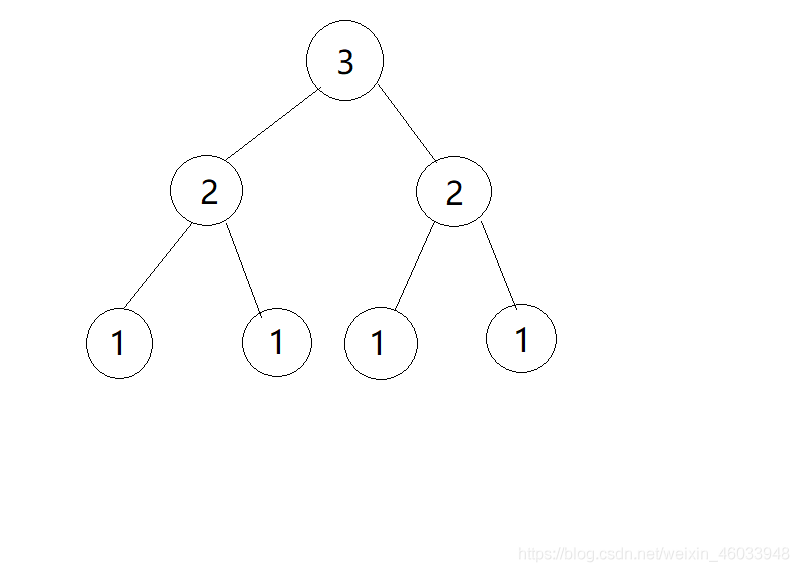
解释：数字代表盘的大小。

对盘子的操作顺序，就是中序遍历这个完全二叉树，可以通过遍历普通的链接存储的二叉树那样的非递归遍历。那我们继续分析，如何才能使用堆栈做一种更简单的遍历。
以上面的图片作为例子，我们做如下思考。
1、在这棵完全二叉树种，叶子节点都是1。
2、3进入堆栈之后出栈不能直接输出，需要等待其子树都产生结束，并且左子树都输出，方可输出。同理2也是，只有1为叶子节点不需要产生后代。要实现产生后代并且等左子树输出之后再输出本节点，必须让其产生后代进栈（进栈的原因：因为后代节点可能依然不是叶子节点），并且本节点也得进栈，因为其输出顺序是：左----根—右，其进展顺序应该是：右—根---左，并且我们得标记其已经产生过后代，等再次出栈到本节点时直接输出。
3、根据第一、二条我们知道，如果碰到叶子节点（不能产生后代）或者已经产生过后代的节点，我们直接输出即可，那么我们就可以节省存储空间不需要单独设置其blag，来标记是否产生过子节点，直接将产生子节点的节点层数修改为1即可。
4、再跟据上面例子的图片，对于根节点n=3，我们需要做的是a->c，根据递归结构的代码我们可以知道其左子树上的2节点应该是a->b，右子树上的2节点应该是b->c。同理我们分析一下当遍历到左子树上的2节点时，其目的是a->b,那么左边的1节点就应该是a->c,右边的节点时c->b。也就是当我们遍历到某节点时，假设本节点应该做的操作是：起点柱->终点柱。那么其左子节点就应该是：起点柱->借助柱；其右子节点就应该是：借助柱->终点柱。如此，在产生子代的过程并修改子代所要做的移动即可。

非递归代码：

#include <iostream>
#include <bits/stdc++.h>
using namespace std; 
typedef struct node
{
    int layer;
    char start;
    char mid;
    char des;
}Node;
node N,t;
int main()
{
    int n;
    cin>>n;
    stack<Node> St;
    N.layer=n;N.start='a';N.mid='b';N.des='c';
    St.push(N);
    while(!St.empty())
    {
        N=St.top();St.pop();
	if(N.layer==1)
	    printf("%c -> %c\n",N.start,N.des);
	else
	{
	    t.layer=N.layer-1;t.start=N.mid;t.des=N.des;t.mid=N.start;
	    St.push(t);
	    t.layer=1;t.start=N.start;t.mid=N.mid;t.des=N.des;
	    St.push(t);
	    t.layer=N.layer-1;t.start=N.start;t.des=N.mid;t.mid=N.des;
	    St.push(t);
	}
    } 
    return 0;
}

递归代码：

#include<stdio.h>
void han(int n,char a,char b,char c)
{
	if(n==1)
                printf("%c -> %c\n",a,c);
	else
	{
		han(n-1,a,c,b);
		printf("%c -> %c\n",a,c);
		han(n-1,b,a,c);
	}
}
int main()
{
	int n;
	scanf("%d",&n);
	han(n,'a','b','c');
	return 0;
}