R语言布朗运动模拟股市、物种进化树状图、二项分布可视化
全文链接：http://tecdat.cn/?p=32393
本文模拟了在连续和离散时间布朗演化一些简单的方法 （ 点击文末“阅读原文”获取完整代码数据 ）。
相关视频
布朗运动的数学模型（也称为随机游动）也可以用来描述许多现象以及微小颗粒的随机运动， 如股市的波动和在化石中的物理特性的演变。
布朗运动是随机模式，即改变了从一次到下一个是随机从正态分布绘制均值为0.0，方差为σ2×ΔT。换句话说，根据布朗运动的预期方差通过时间与瞬时差σ2线性增加。
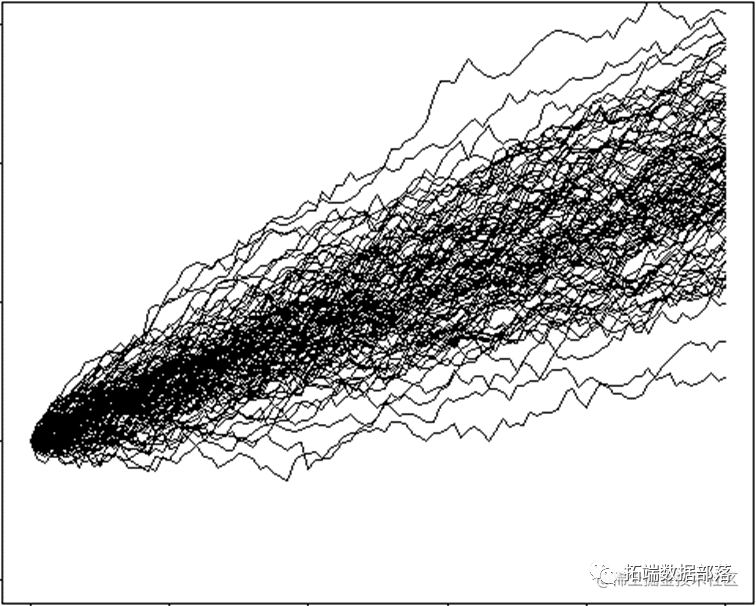
首先，模拟股市一个实例为100的离散时间布朗运动，其中，扩散过程的方差为σ2=0.01。
## 首先模拟随机数
x <- rnorm(n = length(t) - 1, sd = sqrt(sig2))
## 计算累加和
x <- c(0, cumsum(x))
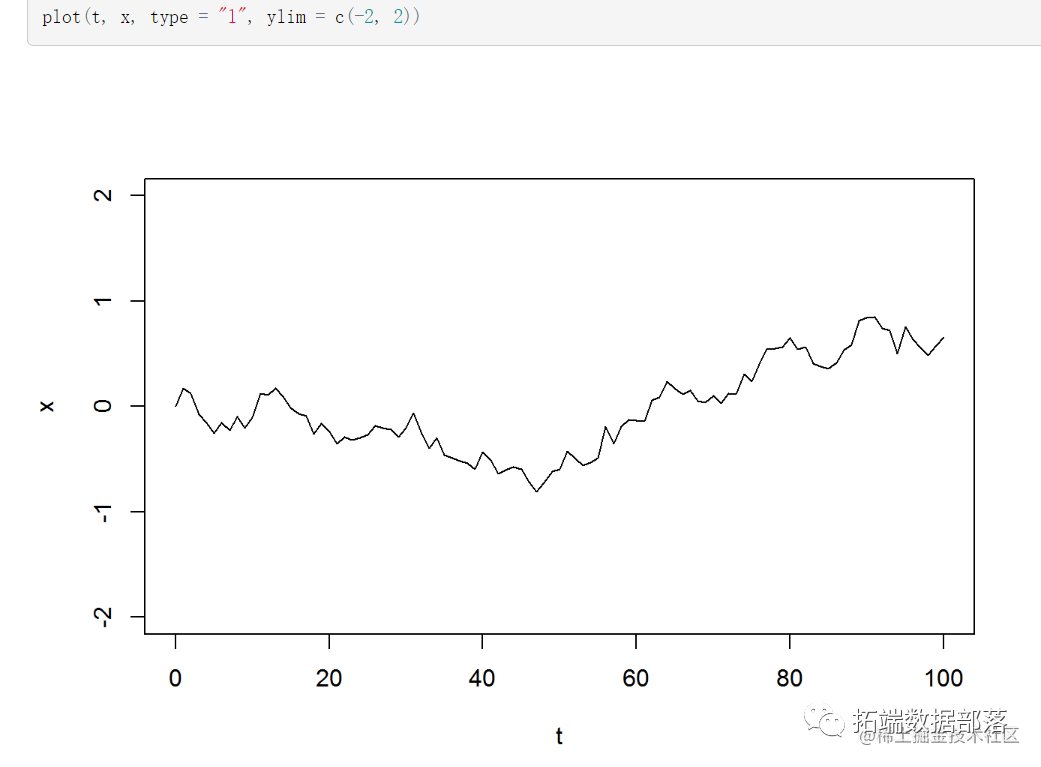
我们得出各t的时间间隔的随机正偏离改变;然后在每个时间间隔，我们计算累积总和。从而可以看出布朗运动的变化的分布是不变的，并且不依赖于时间的状态。
1)
X <- cbind(rep(0, nsim), t(apply(X, 1, cumsum)))
plot(t, X[1, ], xlab = "time", ylab = "phenotype", ylim = c(-2, 2), typ
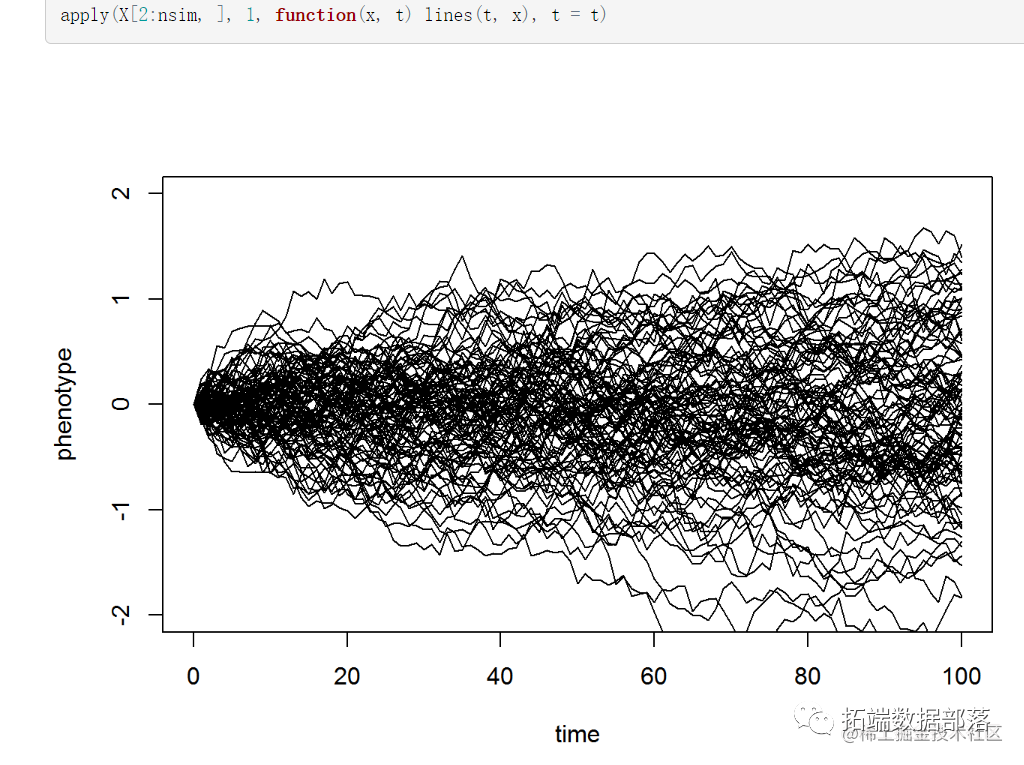
为了看到这结果如何取决于σ2，我们比较除以10 的SIG2的结果：
X <- matrix(rnorm(n = nsim * (length(t) - 1), sd = sqrt(sig2/10)), nsim,
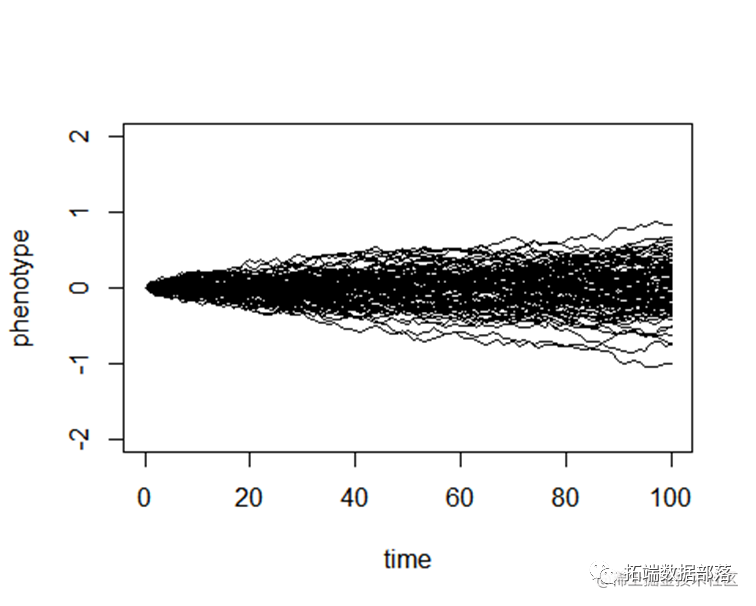
然后，我们使用for循环 ：
e = "l")
for (i in 1:nsim) lines(t, X[i, ])
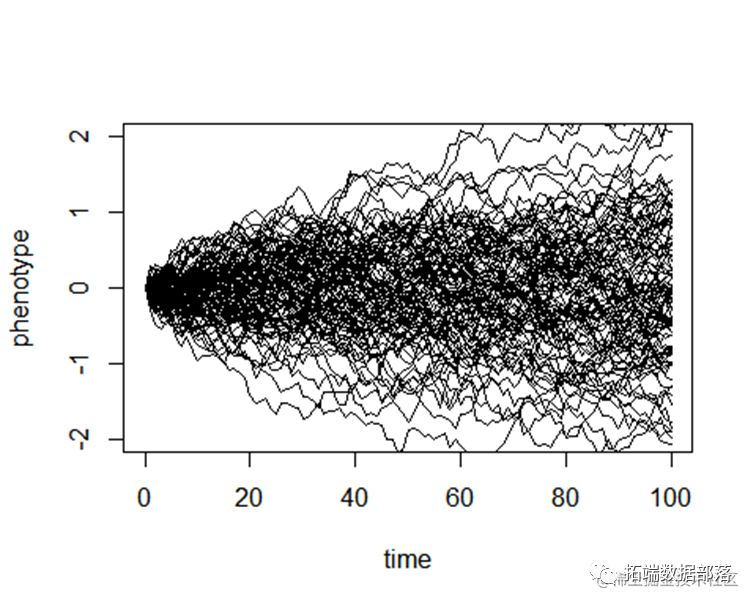
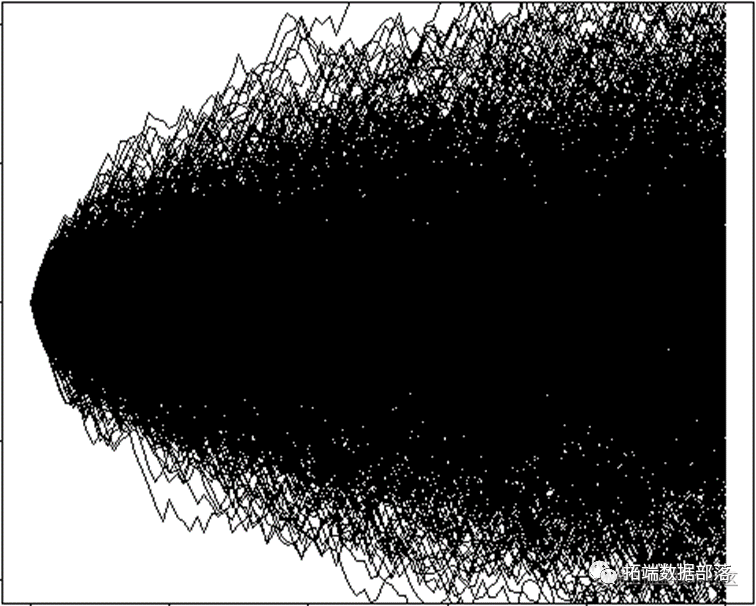
如上所述，根据布朗运动的预期方差只是σ2。然后，我将使用模拟10000个相同的条件下的结果，以“理顺”我们的结果是：
v <- apply(X, 2, var)
plot(t, v, type = "l", xlab = "time", ylab = "variance among simulation
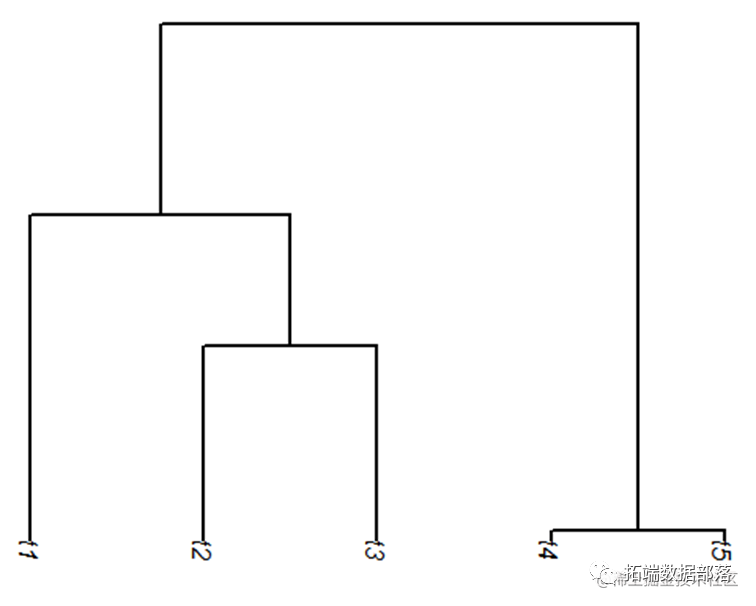
然后，我们尝试用布朗运动模拟物种进化树状图。查看数据的变化情况：
t <- 100 # 总时间
n <- 30 # 总分支
b <- (log(n) - log(2))/t
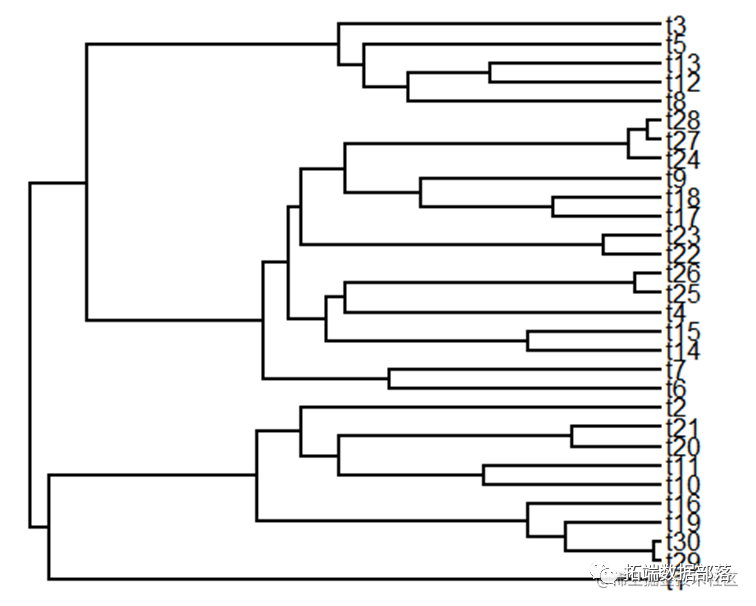
现在，来模拟树，我们只需要分别模拟在每个分支的所有分支，然后由最终状态“转向”每个子分支它的父节点。因为在每个时间步布朗进化的结果是独立于其它所有时间步长。
沿着每条边模拟进化
yy <- sapply(yy, function(x, y) y[[x]][length(y[[x]])], y = X)
text(x = max(H), y = yy, tree$tip.label)
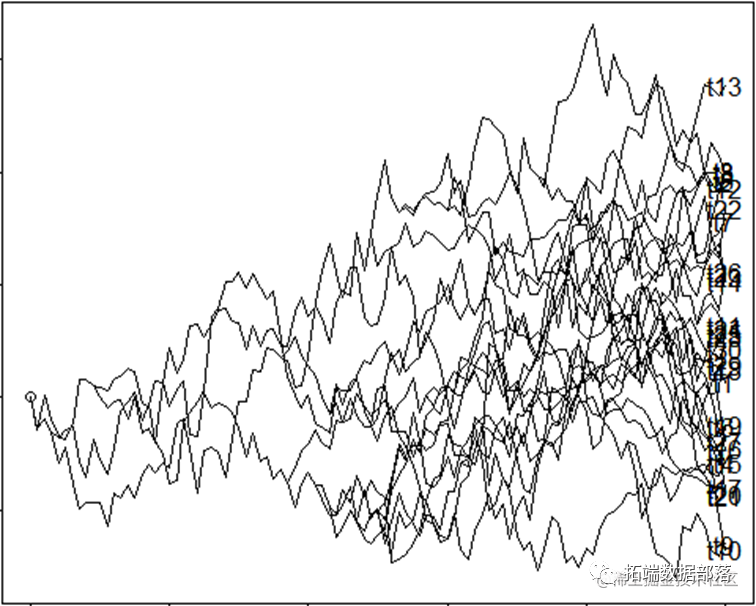
在现实中，布朗运动的大部分模拟使用连续的而不是离散的时间进行。这是因为布朗运动意味着不同物种之间的协方差之间的预期差异。
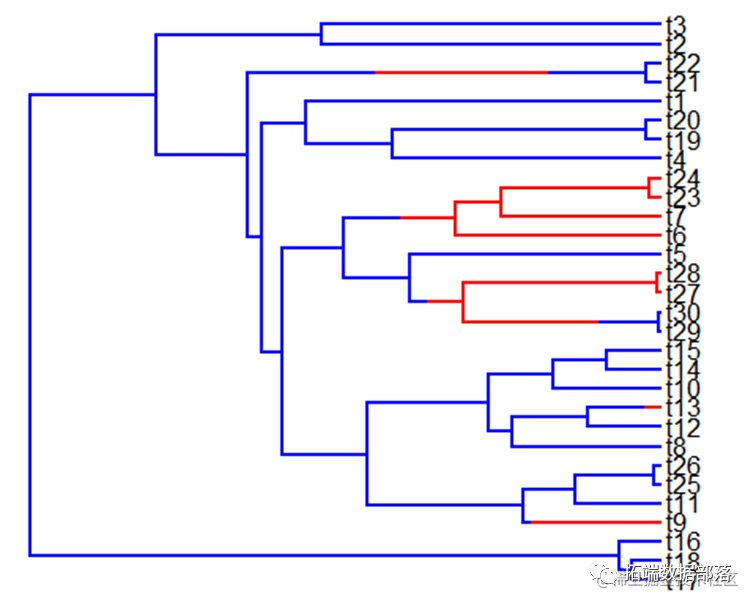
关于布朗进化的一些其他特点：在某些情况下，在树的不同部分的布朗进化有可能存在不同的速率。因此可以简单的模仿不同部门的不同的速率布朗运动。
tree <- sim.history(tree, Q, anc = "1")
点击标题查阅往期内容
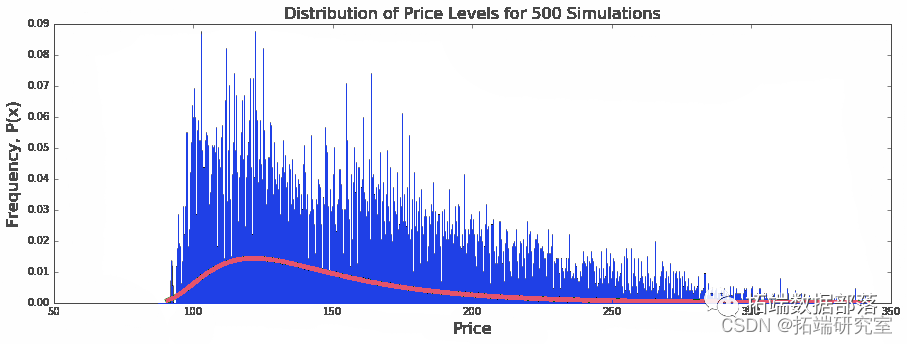
PYTHON 用几何布朗运动模型和蒙特卡罗MONTE CARLO随机过程模拟股票价格可视化分析耐克NKE股价时间序列数据
左右滑动查看更多
01
02
03
04
els = TRUE,
spread.cost = c(1, 0))
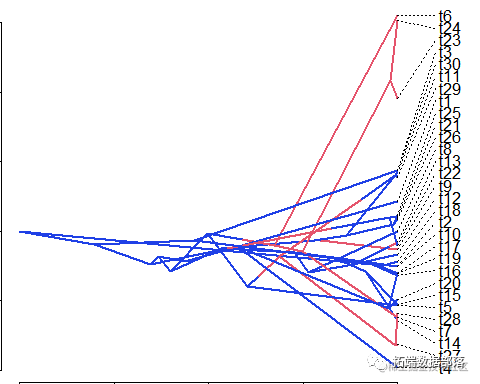下面模拟不同的树从而通过散点图证实相同的父节点产生的树拥有相似的协方差。
plot(tree, edge.width = 2, direction = "downwards")
rplotMatrix(t(X))
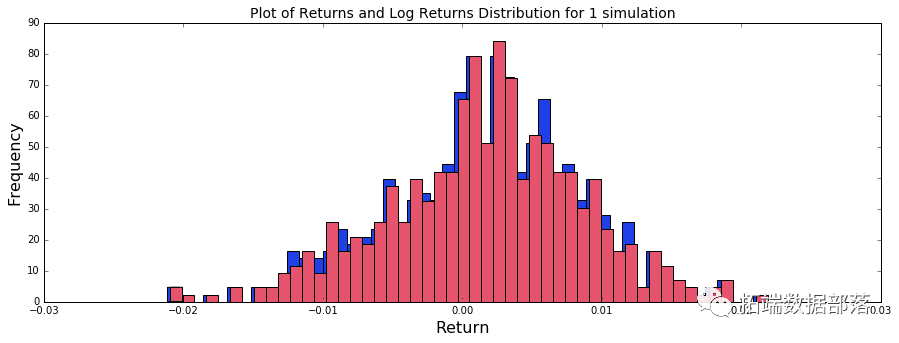
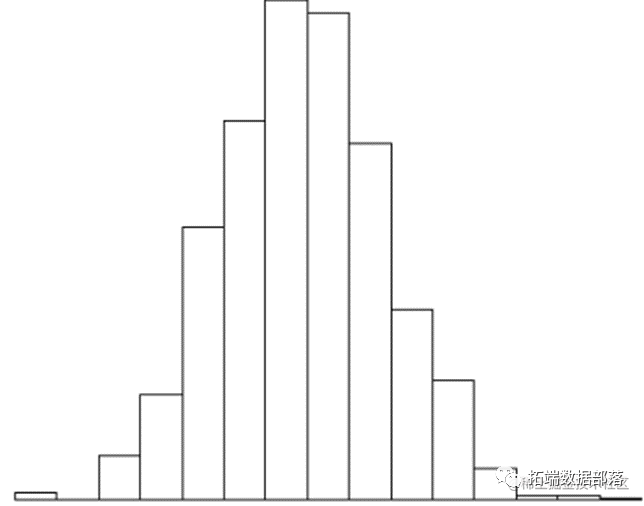
布朗运动不假定在其下个体谱系移动的过程是高斯过程。其结果将服从高斯分布 - 和中心极限定理。
t <- 0:100
sig2 <- 0.01
nsim <- 1000
二项分布的布朗运动
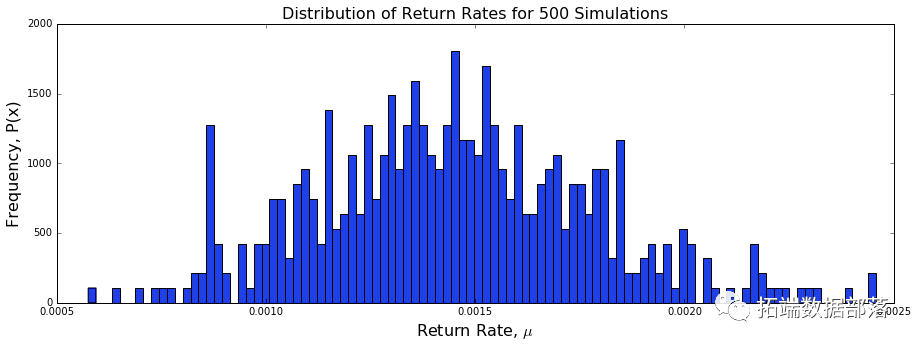
我们模拟二项分布的布朗运动 并查看方差是否和之前一样等于1：
apply(X[2:nsim, ], 1, function(x, t) lines(t, x), t = t)
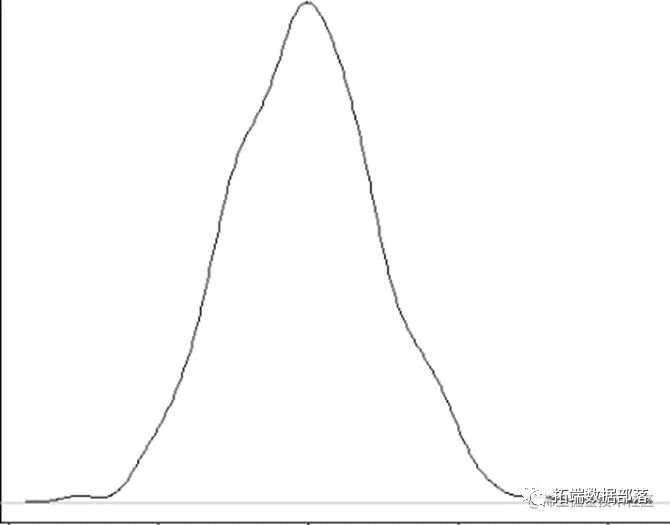
布朗运动，一般认为是没有趋势;然而它（在某些情况下）可以模拟一个模型的趋势。这里是一个模拟（使用如上述相同的一般方法）趋势的一个例子。
X <- matrix(rnorm(mean = 0.02, n = nsim * (length(t) - 1), sd = sqrt(sig2/4)),
nsim, length(t) - 1)
对于布朗运动的数学模型的简单形式的形式：S_T= eS_t-1 其中e是从概率分布绘制。因此，后续还有更多的应用值得进一步研究。
点击文末“阅读原文”
获取全文完整代码数据资料。
本文选自《R语言布朗运动模拟股市、物种进化树状图、二项分布可视化》。
点击标题查阅往期内容
R语言做复杂金融产品的几何布朗运动的模拟MATLAB用COPULA模型进行蒙特卡洛(MONTE CARLO)模拟和拟合股票收益数据分析
python中的copula：Frank、Clayton和Gumbel copula模型估计与可视化 R语言中的copula GARCH模型拟合时间序列并模拟分析
matlab使用Copula仿真优化市场风险数据VaR分析
R语言多元Copula GARCH 模型时间序列预测
R语言Copula函数股市相关性建模：模拟Random Walk(随机游走)
R语言实现 Copula 算法建模依赖性案例分析报告
R语言ARMA-GARCH-COPULA模型和金融时间序列案例
R语言基于copula的贝叶斯分层混合模型的诊断准确性研究
R语言COPULA和金融时间序列案例
matlab使用Copula仿真优化市场风险数据VaR分析
matlab使用Copula仿真优化市场风险
R语言多元CopulaGARCH模型时间序列预测
R语言Copula的贝叶斯非参数MCMC估计
R语言COPULAS和金融时间序列 R语言乘法GARCH模型对高频交易数据进行波动性预测
R语言GARCH-DCC模型和DCC（MVT）建模估计
Python使用GARCH，EGARCH，GJR-GARCH模型和蒙特卡洛模拟进行股价预测
R语言时间序列GARCH模型分析股市波动率
R语言ARMA-EGARCH模型、集成预测算法对SPX实际波动率进行预测
matlab实现MCMC的马尔可夫转换ARMA - GARCH模型估计
Python使用GARCH，EGARCH，GJR-GARCH模型和蒙特卡洛模拟进行股价预测
使用R语言对S＆P500股票指数进行ARIMA + GARCH交易策略
R语言用多元ARMA,GARCH ,EWMA, ETS,随机波动率SV模型对金融时间序列数据建模
R语言股票市场指数：ARMA-GARCH模型和对数收益率数据探索性分析
R语言多元Copula GARCH 模型时间序列预测
R语言使用多元AR-GARCH模型衡量市场风险
R语言中的时间序列分析模型：ARIMA-ARCH / GARCH模型分析股票价格
R语言用Garch模型和回归模型对股票价格分析
GARCH（1,1），MA以及历史模拟法的VaR比较
matlab估计arma garch 条件均值和方差模型
R语言ARMA-GARCH-COPULA模型和金融时间序列案例
