MIT博士生杨珩：从L1到L5，自动驾驶的“拦路虎”可能是一个数学问题-技术圈

大数据文摘授权转载自AI科技评论

作者 | 陈彩娴

什么叫做「可认证感知算法」（Certifiable Perception Algorithm）？它对自动驾驶，或其他机器人（Robotics）方向的研究意义是什么？它的研究难点又是什么？

事实上，「可认证感知算法」最早是一个数学上的概念，在2016年由苏黎世联邦理工学院（ETH）数学系的教授、2018年斯隆研究奖获得者 Afonso S. Bandeira 在“A Note on Probably Certifiably Correct Algorithms”一文中提出。

针对许多优化问题在获得一个解时、没有后验（a posteriori）证明该解是否为最优解的情况，Bandeira 提出了一个 PCC（Probably Correct Certifiable）算法，不仅可以解决经典的优化实例问题，还可以提供一个「后验证书」（a posteriori certificate），向研究人员证明该解为最优解。

在 Bandeira 的这篇工作中，PCC算法也被应用于机器学习的某些场景，比如学习随机块模型（stochastic block model）。本质上，“certificate”是一个数学测度，揭示了研究人员求得的解与全局最优解之间的差距。例如，当差距非常小，只有一亿分之一时，那么研究人员就能知道，该解已是近似最优，可以视为全局最优。

受此启发，杨珩从2018年开始研究可认证感知算法，如今已取得一系列成果。

1. 什么是可认证算法？

在自动驾驶中，可认证感知算法存在的核心意义，是提高车辆在驾驶过程中的安全性，防止意外事故的发生。

如下图所示，自动驾驶车辆A（即“robot”，机器人）在路上行驶的过程中，如“看”到一辆车B，用摄像头拍摄一张照片，照片中会包含该车辆 B。我们假设车辆A的内存里有B的3D模型，而车辆A的任务是估测B的位置和姿态（6D pose, 3D rotation and translation）。这时，A 会用一个神经网络检测出所摄2D平面图像上的所有关键点（keypoints），如车轮、车灯、镜子等等，然后将这些所识别出的目标与3D模型上的关键点进行数据关联（data association），识别物体是车镜、车灯或其他元件。

如果神经网络所检测出的关键点与数据关联都是正确的，那么自动驾驶的视觉感知挑战（比如估测车辆B的位置和姿态）在转为数学优化问题时则相对好解。但在实践中，神经网络往往会出错。神经网络的前端可能会输出错误的关键点，比如，有可能将检测出来的镜子识别为汽车的轮子，从而建立一些不正确的关联，也就是所谓的「异常值」（outliers，上图的红色连线）。

在这种情况下，我们往往难以区分 2D 平面图像与 3D 汽车模型中的对应关系中，哪些是正确数据（inliers）、哪些是异常数据（outliers）。这时，自动驾驶车辆 A 在估测车辆 B 的姿态时，如果估计正确，那么线框图会对应地重叠在 A 所拍摄的 2D 图像上；若估计错误，则 2D 图像上会出现许多红点（如上图最右上角所示）。

一旦估计出错，自动驾驶车辆则可能发生碰撞等安全事故问题。比方说，自动驾驶车辆A感知到同时行驶在一条马路上的车辆 B 的存在。B 距离 A 实际只有3米，但如果估计错误，判断 B 距离 A 有10米，那么 A 可能就会加速行驶，造成严重的事故。

所以，用于估计车辆姿态的算法不仅要告诉研究人员一个正确的结果，还要解释这个结果有多么地正确（即解与最优解之间的距离）。当算法失败时，算法也应向驾驶自动车辆的人（或者系统）传递一个信号，使驾驶员能采取其他的行动，比如接管方向盘、停车或及时寻求他人支援等。这，也是「可认证感知算法」的具体内涵。因此，在「安全第一」的自动驾驶领域，可认证感知算法具有深远的现实意义。

但话说回来，「可认证算法」所扮演的角色虽然听起来很简单，研究起来却并不容易，因为在这个研究的过程中涉及到了对截断最小二乘法（Truncated Least Squares, TLS）的求解。TLS是一个非凸优化问题，其可行域集合可能存在局部最优点，但求解全局最优的难度相当于NP难题。

因此，尽管早期欧洲有些学校也沿着可认证算法的方向研究，但他们解决问题的切入点只停留在建模阶段，且面向的场景为没有异常值的情况。

基于Bandeira的工作，杨珩与他的博士导师 Luca Carlone 还就「可认证算法」制定了更高的标准。

假设算法为 A，A 的目标是解决优化问题 P，而优化问题取决于输入数据 D。那么，如果该算法是可认证的，则必须同时满足三个条件：

1）A 必须是多项式算法（polynomial algorithm），理论上必须要快；

2）在解决 P 后，A 要么得到一个全局最优解，以及证明该解为全局最优的“证书”（certificate）；要么失败，没有得到全局最优解，只得到所谓的“measurable suboptimality”，即所求得的解与全局最优解之间的距离；

3）对于大部分 D，A 都能将 P 解到全局最优。

第三个条件由杨珩与 Luca Carlone 添加，目的是为了排除近似算法。所谓“近似算法”（approximate algorithm），指的是算法得到的解永远只能是近似最优。在自动驾驶中，近似算法相当于在任何情况下都无法取得全局最优解，一直“报错”，这会对驾驶安全造成极大隐患。

所以，在杨珩与团队的假设中，A 只有在处理大多数不同情形时能得到全局最优解，才能被称为「可认证算法」，满足自动驾驶的安全需求。

2. “非凸”转“凸”

2018年12月，杨珩加入麻省理工学院信息与决策系统实验室（Laboratory for Information & Decision Systems, LIDS），师从MIT莱纳多职业发展副教授 Luca Carlone，开始从事计算机视觉与机器人的结合研究。

一开始，他们只是从一个小的点云配准/重建（point cloud registration）问题出发。所谓“点云配准”，指的是求两个点云之间的旋转平移矩阵，将源点云变换到与目标点云相同的坐标系下。比如，一辆车无人车分别处在 a 点与 b 点，用无人车点雷达分别对着一栋楼扫一下，再把两张扫描的图融合在一起。

他们针对这个问题设置了一个可认证算法，并在2019年1月投了一篇文章到机器人顶会 RSS（Robotics: Science and System），文章被接收。在这篇工作中，他们使用TLS来重新设计点云优化估测问题，使估计对大部分虚假的点到点对应关系不敏感，可以容忍高达 99% 的异常值（outliers）。

图注：杨珩被 RSS 2019 接收的工作，论文地址为 https://arxiv.org/pdf/1903.08588.pdf

但是，他们在 RSS 2019 中提出的可认证算法精确度并不够突出，有时无法满足上述所说的第三个条件（对大部分输入数据都能获得最优解）。许多时候，该算法得到的差距至多是 1e-2、1e-3，而不是1e-6或1e-10等接近0的差距。

从 RSS 2019 开始，他们就一直在研究可认证算法。

2019年2月左右，杨珩用两周时间独自琢磨，看了许多数学资料，尝试换一种对原问题（TLS）的求解方法。他从一个数学思维出发，提出了半正定规划（Semidefinite Programming）松弛，将非凸优化问题 TLS 转化为凸优化问题。这个方法十分成功，他们投到了 ICCV 2019，被成功接收。

图注：杨珩被 ICCV 2019 接收的工作，论文地址为 https://arxiv.org/pdf/1905.12536.pdf

对杨珩来说，ICCV 2019 的这篇工作有里程碑式的纪念意义：

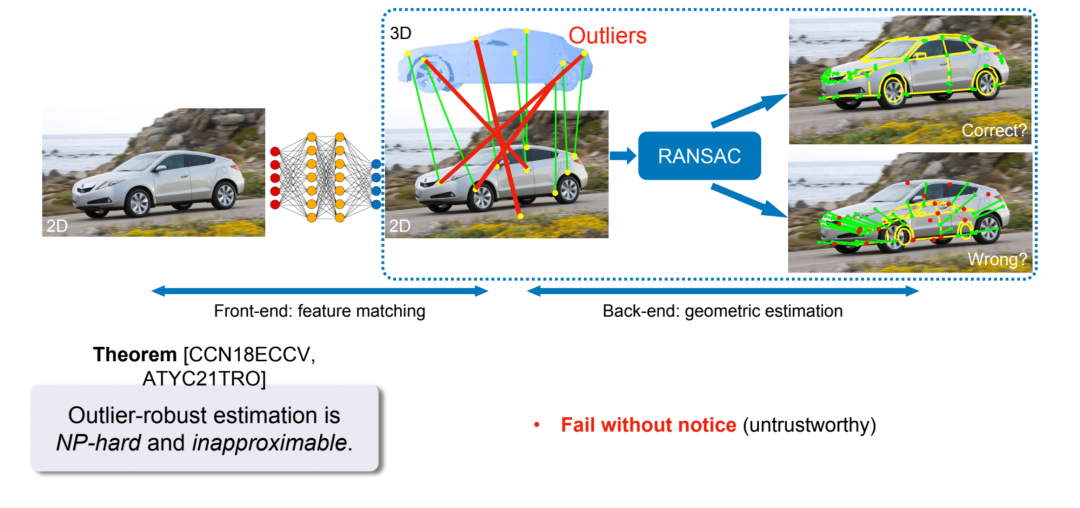
因为那篇文章是第一个能将有异常值（outliers）的机器人感知问题在多项式时间内（polynomial time）解到全局最优（global optimality）的工作。我们设计的半正定规划松弛（SDP relaxation）是extremely tight，那个算法几乎对所有问题都能得到全局最优，而且它解的原问题是一个带有二元变量（+1 和 -1，mixed integer）的非凸问题。这种问题是一个NP-hard问题。

Wahba 问题，又称为“旋转搜索”，旨在找到最佳旋转以在给定的对应关系下对齐两组向量观察，是许多计算机视觉和机器人应用中的基本研究（比如可以用作卫星的定位）。在 ICCV 2019 中，杨珩针对大量向量观测值为异常值（outliers）的情况，提出了第一个多项式时间可证明的最优方法来解决 Wahba 问题。

在这篇工作中，除了使用 TLS 成本来制定 Wahba 问题，他们还开发了凸半定规划（SDP）松弛来解决非凸问题。他们提出可认证算法 QUASAR （基于 QUAternion 的半定松弛法，用于鲁棒对齐），即使在面临大量噪声与异常值的情况下（比如多余95%的异常值），他们的松弛也很“紧”，算出可证明的全局最优解（即松弛是精确的），优于鲁棒的局部优化算法 RANSAC。

“非凸”转“凸”，是杨珩提出的算法能够在大部分输入数据中求得全局最优解的关键点。凭借这一主导思想以及后续的一系列工作，杨珩获得 ICRA 2020 的机器视觉最佳论文奖，还入围了 RSS 2021 最佳论文奖最终名单。

如前所述，TLS是一个非凸优化问题，基本框架如下：

非凸问题几乎是无法快速求得全局最优解的，但是，我们可以通过凸松弛方法，将非凸问题转为凸问题。这个过程就相当于以退为进：当你面对一道难题（如非凸问题）、不知所措时，你可以先把它转化成一个较为简单的问题（如凸问题），然后去求解这个简单的问题。解完简单的问题后，你会知道简单的问题 B 与原问题 A 是否等价。

更有意思的是，在解出简单问题 B 之前，你并不知道简单问题 B 是否与难问题 A 是否等价。但当你解完 B 后，你会检验该解是否满足原问题的某些条件、从而推测问题 B 与问题 A 是否等价。如果满足，那么凸问题被解，实际上也就意味着原来的非凸问题已经解决。

「有点“事后诸葛亮”的感觉。」杨珩形容。从理论上讲，一般性的凸问题也是NP-hard问题，目前在多项式时间内是不可求解的，但极个别凸问题，比如SDP的优点是：可以在多项式时间内求出全局最优解。在这个凸问题中，所有局部最优都是全局最优。

在“非凸”转“凸”的过程中，杨珩的灵感也源自一个非常著名的数学“松弛”理论：2001年，法国数学家 Jean B. Lasserre 在数学顶刊《SIAM Journal on Optimization》上发表了一篇著名的文章，叫“Global optimization with polynomials and the problem of moments”（引用量已超过2600），里面提到：

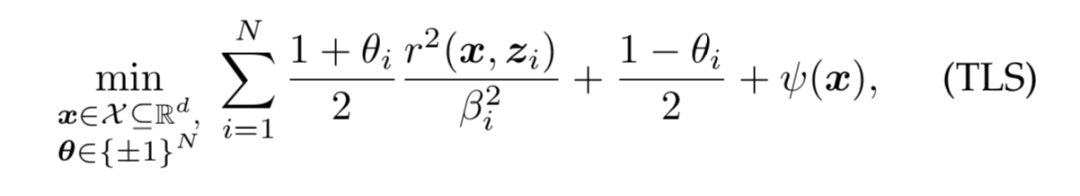
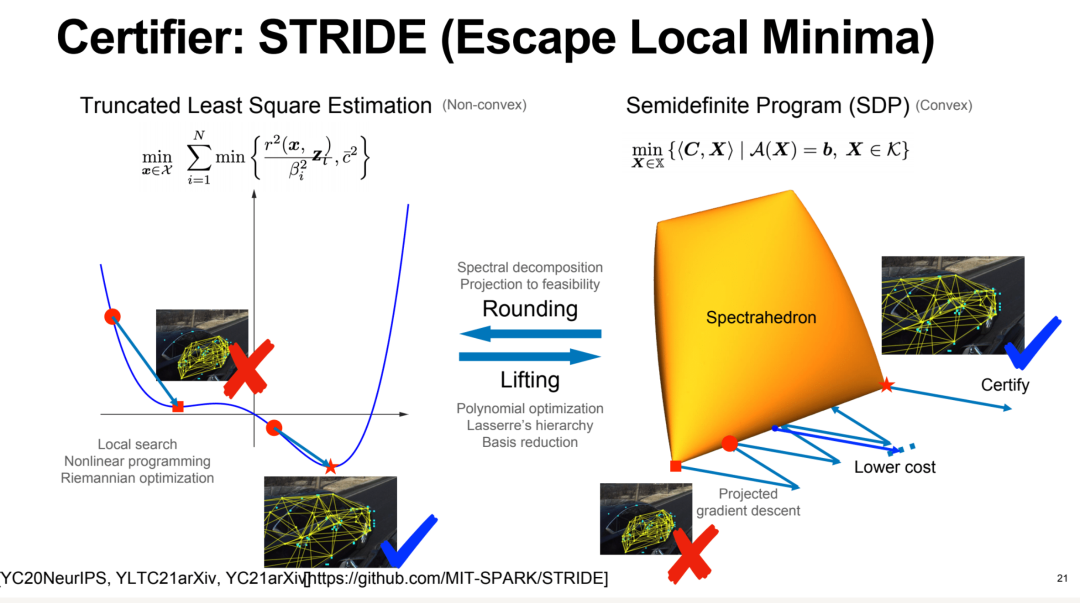
非凸问题永远不可能等价于凸问题，但如果满足一定条件，我们就可以用一个足够大的凸问题来逼近/解决一个非凸问题。不过，我们并不明确该非凸问题有多大，它可能是无限大。

这是一个十分优美的理论。假设非凸问题是迷雾中的一座小岛，那么凸问题就是一片不断在寻找岛屿边界的汪洋，摸索，定义，直至几乎全部包围，不断接近真实的全貌。

但也不难推测，在这个“松弛”的过程中，研究会面临两个难点：

1）如何用一个足够小的凸问题来解决非凸问题？比方说，原来的非凸问题可能只有100个参数要求解，但你要解的凸问题可能有100万个参数。也就是说，你需要解一个非常大的凸问题，才能解原来的非凸问题。

2）杨珩观察到，虽然只要解决一个包含100万参数的凸问题、就能解原来只有100个参数的凸问题，但目前在数学上，没有一个求解器可以解决这么大的凸问题。在杨珩的研究中，他所用于求解非凸问题的凸问题是“半正定规划”问题（Semidefinite Programming, SDP），属于凸问题里最难的一类。

从理论上讲，要解决原来的非凸问题 TLS，转换的凸问题可能要无限大，不止100万个参数，也可能是1000万、1亿、10亿甚至上百亿。针对第一个难点，杨珩及团队用真实计算显示：转化的凸问题（即SDP问题）不需要无限大，只需要一个最小的凸问题（参数量为100万)，即可解决原来的非凸问题。

而且，在将非凸问题（下图左）转为凸问题（下图右）的过程中，算法不仅在凸问题上求解，还会将凸问题的解投射到原来的非凸问题中，来回求解。在这个过程中，非凸问题的解会加速凸问题的求解，非凸问题的局部最优也可以映射到凸问题的顶点（vertexes），加速求解。目前，他们的工作是第一次在SDP求解中用到了这种「不舍原问题」的求解思想，极具创新。

而对于第二个难点，杨珩他们所面临的难点是：目前市面上现有的求解器最多只能求解规模为小到中等的 SDP 问题。所以，他们只能自己研发求解器。

3. 研发求解器 STRIDE

找到全局最优解，与证明全局最优解，是两码事。比如，在ICRA 2020的机器视觉最佳论文奖中，杨珩所提出的算法便能快速找到全局最优解，但是无法证明该解是全局最优，即找不到一个明确的“证书”（certificate）来佐证。

杨珩解释，从本质上看，Robotics（关于机器的学科）的核心是优化，车辆的3D姿态估计便是在解一个优化问题。不仅是感知，自动驾驶中的车辆控制、规划等，都是在解决优化问题。

针对不同的优化问题，研究人员会使用不同的优化框架，并根据某个特定的框架寻找是否有合适的求解器。研究分为两步进行：建模（modeling）与求解（solving）。

所谓「建模」，就是将一个真实世界的问题（如上述所说的自动驾驶汽车感知周围事物）转化为一个数学问题。建模完成后，解决这个数学优化问题的过程就叫做「求解」。一般情况下，目前在机器人（Robotics）领域，大多数工作都是只做建模，仅依靠现存的求解器来解决数学上的优化问题。杨珩的博士导师 Luca Carlone 此前便主要做建模。

但在研究可认证算法的过程中，他们发现，如果只做建模是无法解决100万参数量的问题。市面上也没有成熟的SDP求解器可以帮助他们解决这个问题，所以他们只能自己去开发求解器。

从2019年开始，他们就在寻找适合的求解器。一开始，他们的问题也没有包含那么多的变量，现有求解器已能满足这个凸问题的计算要求。直到去年9月，他们的研究要面临越来越多的参数量，才发现「还是得自己开发求解器，因为现有的求解器解决不了我们的问题。」

从去年9月到今年4月，他们一直在尝试不同的求解器，发现结果均不尽如人意。于是，他们就去找了新加坡国立大学数学系的系主任 Kim-Chuan Toh 和他的学生 Ling Liang，与他们一起合作，针对待解凸问题的特质，用大约 4 个月的时间开发出了一个主要面向 SDP 问题的约束求解器——STRIDE。（STRIDE的源码目前已在Github上公开：https://github.com/MIT-SPARK/STRIDE）

开发求解器的难点，主要是利用好待解决问题的优势。半正定规划（SDP）是一个很大的数学问题，而杨珩要解决的SDP问题除了通用特征，还有一些特殊的性质。比如，它的最优解是低阶（low rank）。

而有了 STRIDE 的助力后，杨珩所提出的可认证感知算法在求解速度与准确度上均有了明显的提升。

如下图所示，原来的非凸问题 TLS 只有 54 个变量时，它所对应的凸问题 SDP 至少有 8154 个变量；TLS 只有 1004 个变量时，SDP 问题的变量超过了 300 万。MOSEK 与 SDPT3 被视为目前最出色的 SDP 求解器，但随着问题的变量越来越多，MOSEK 与 SDPT3 不仅无法求解，甚至连存储该问题的内存都没有。

在上图中，1e-10、1e-12等数值为精确度。数值越低，求解的精确度越高。从第 1 行到第 5 行，优化的问题越来越大，测度（measurement）越来越多。回到一开始的例子，就是自动驾驶车辆周围的汽车越来越多，汽车的关键点与连线也会越来越多。

实验证明，当问题的维度（dimension）较低时，SDPT3 和 MOSEK 可以求解，但速度不到 STRIDE 的二分之一。比如，在维度为 104 时，MOSEK 的求解时间是 870 秒，而 STRIDE 只需 45 秒；维度为 204 时，MOSEK 无法求解，而其他算法虽然可以解，但却解不到全局最优，精确度不够。当维度达到 1004 时，即使给再多的运行时间，其他求解器也无法达到与 STRIDE 相匹配的精确度。

杨珩介绍，他们所提出的算法是目前唯一能够解决大规模一阶（rank-one）SDP问题的方法。他们在百度的自动驾驶数据集 Apollo Scape （图像采集自北京、上海与深圳）上做过实验，STRIDE 的性能明显优于 MOSEK 等求解器。

此前，他们的工作曾发表在 NeurIPS 2020 上，但当时，算法只解决了 4 个常见的感知问题。加上 STRIDE 后，他们尝试将算法拓展至更广泛的设置下进行，解决了 6 个感知问题，包括单点旋转均匀（single rotation averaging）、多点旋转均匀（multiple rotation averaging）、点云配准、网格配准、绝对姿态估计与分类感知。

求解器的核心思想是优化与决策，而自动驾驶的运行就是“robot”（汽车）一直在做决策。比如，自动驾驶车辆要从 a 点走到 b 点，而 a 点与 b 点之间有一个障碍物，那么，规划一条从 a 点到 b 点的最短路线，便是一个近似优化问题。

杨珩还介绍，STRIDE求解器不仅可以解决机器视觉问题，还有望解决一些数学问题。他们最近做了一些新的工作，便计划投到数学类的期刊与会议上。

4. 数学不可或缺

目前，杨珩的工作还处于学者讨论的阶段，距离落地还有一段很长的距离。

尽管他们的算法在求解速度上已经很快，但实际的求解时间也要 1 个小时。如果可认证算法要在现实中落地，那么求解时间至少要从 1 个小时缩减到 1 秒。

「很多人认为自动驾驶很简单，那或许是因为他们还没有体会到数学和科学计算有多难。」杨珩感叹，「从 L1 到 L5，自动驾驶要解决的都是数学问题。越来越多人发现，自动驾驶不是只依靠神经网络就能成功。」

尽管如此，杨珩的可认证感知算法仍有存在的意义：「我可以认证，只是我现在认证的时间比较长而已。」在未来，计算硬件的提升可能会带来问题的突破。

对杨珩等痴迷理论研究的科研者来说，在研究可认证算法的过程中，「非凸」转「凸」的成功，才是一件比求解时间从 1 小时缩减到 1 秒更令人激动的突破。

在研究的过程中，杨珩受到许多数学知识的帮助与启发，也取得了不少突破性的成果。因此，他觉得数学在视觉算法研究（和其他科学研究）中是一门十分重要的学科：

硬核数学问题会非常考验人的耐心。我觉得有时候也不是难不难的问题，而是你能不能花一天的时间看一篇数学文章，搞懂这篇文章的所有细节。有可能你看了5遍之后，你就会醍醐灌顶。在那一瞬间，这个方法成为了你自己的方法。一旦你掌握了这个方法之后，你就会发现这个方法特别地 powerful（强大），可以将它应用到很多别的方案中。
如果有一天，你能想明白数学家是怎么理解问题的，可能你的境界就高了一层。

谈到未来的研究方向，杨珩的愿望之一是用可认证算法来指导神经网络的训练过程，提高神经网络的安全性。

少年新马，未来可期。

参考链接：

1. A. Bandeira. A note on probably certifiably correct algorithms. Comptes Rendus Mathematique, https://arxiv.org/pdf/1509.00824.pdf

点「在看」的人都变好看了哦！