六十、走进位运算的大门
「@Author:Runsen」
❝编程的本质来源于算法,而算法的本质来源于数学,编程只不过将数学题进行代码化。「---- Runsen」
❞
根据我的脑海大纲,现在应该进入位运算的大门。
位运算,计算机内所有的数都以二进制存储,位运算是对二进制位的操作。
按位“与”运算
按位“与”运算的运算符是:&。首先我声明一个变量i等于11,j等于2,然后我们计算i和j的按位“与”运算,也就是11&2,得到的结果是2.‘
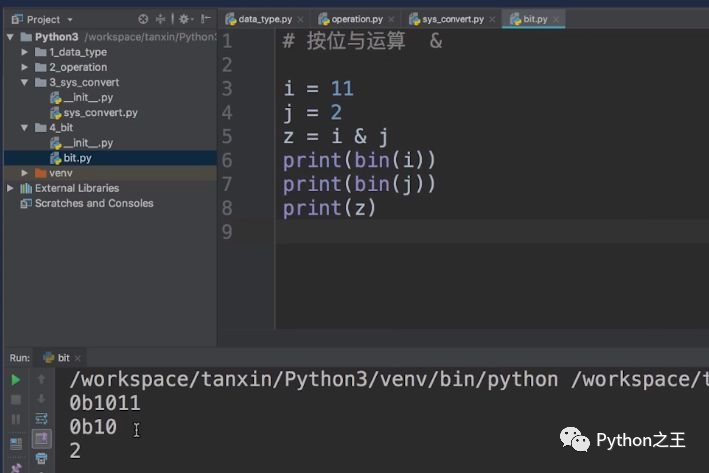
个2是怎么来的,首先我们要把这个11和这个2全部转换成二进制,我们从上图看出11的二进制是0b1011,2的二进制是0b10。0b这个它就是一个二进制的标识位,就是告诉我们这个是二进制。
按照位“与”运算的原则,如果两个值相应的位置都为1也就是上下都为1的时候,那么该结果就是1,如果有一个不是1,那么就是0
1011
0010
----
0010
所以,1011和0010的按位“与”运算就是0010,然后将二进制的0010转化为十进制,就是我们的结果2。
按位“或”运算
下面,我们介绍按位“或”运算。按位“或”运算的运算符是:|。我们同样计算11和2的按位“或”运算,得到的结果是11。
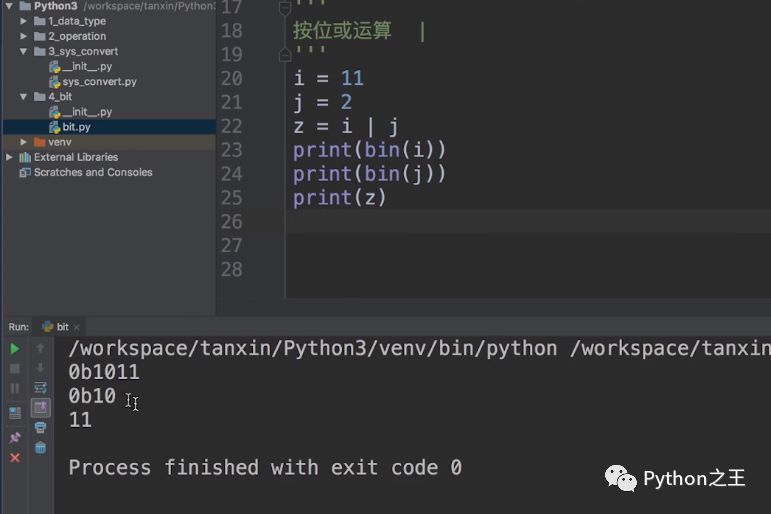
这个结果2到底是怎么样来进行运算的?11的二进制是1011,而2的二进制是0010。
按照位“或”运算的原则,如果两个值相应的位置有一个是1,那么该结果就是1,也就是如果都是0,该结果就是0
1011
0010
----
1011
所以,1011和0010的按位“与”运算就是1011,然后将二进制的1011转化为十进制,就是我们的结果11。
按位“异或”运算
下面,我们介绍按位“异或”运算。按位“异或”运算的运算符是:^。我们同样计算11和2的 按位“异或”运算,得到的结果是9。
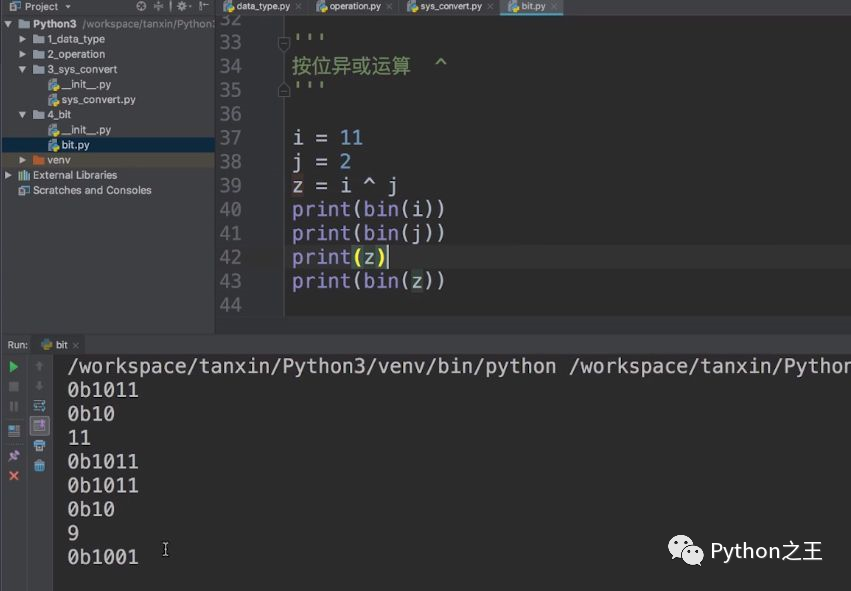
这个结果9到底是怎么样来进行运算的?11的二进制是1011,而2的二进制是0010。
按位“异或”运算的原则,如果两个值相应的位置相同1,那么该结果就是0,也就是如果都是0或者都是1,该结果就是0.同样只有是1和0,那些结果就是1
1011
0010
----
1001
所以,1011和0010的按位“异或”运算就是1001,然后将二进制的1001转化为十进制,就是我们的结果9。
按位取反运算
下面,我们介绍按位取反运算。按位“异或”运算的运算符是:~。我们计算11的按位取反运算,得到的结果是-12。
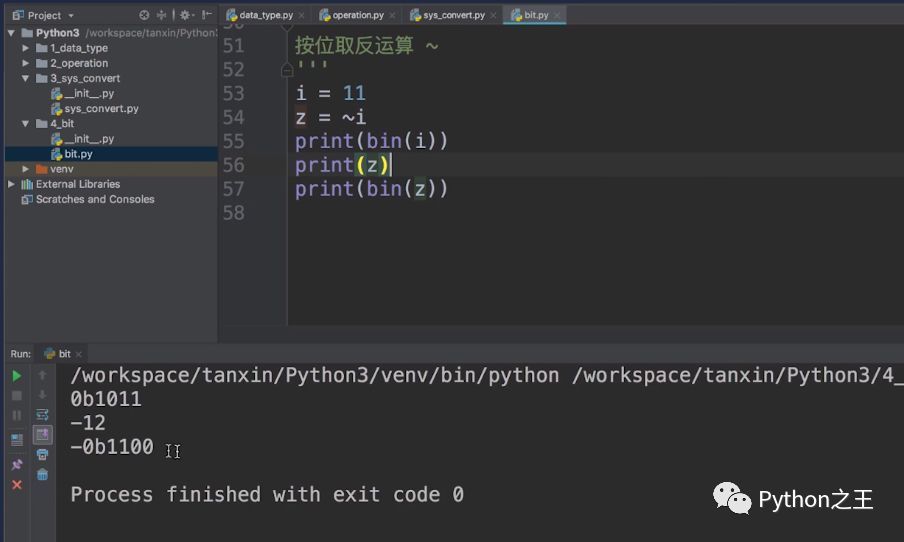
这个结果-12到底是怎么样来进行运算的?按位取反的计算结论是:~n = -(n+1)
因此,11的按位取反运算 :~11=-(11+1)=-12
左移运算符
下面,我们介绍左移运算符。左移运算符是:<<。我们计算11的左移2位的运算,得到的结果是44。
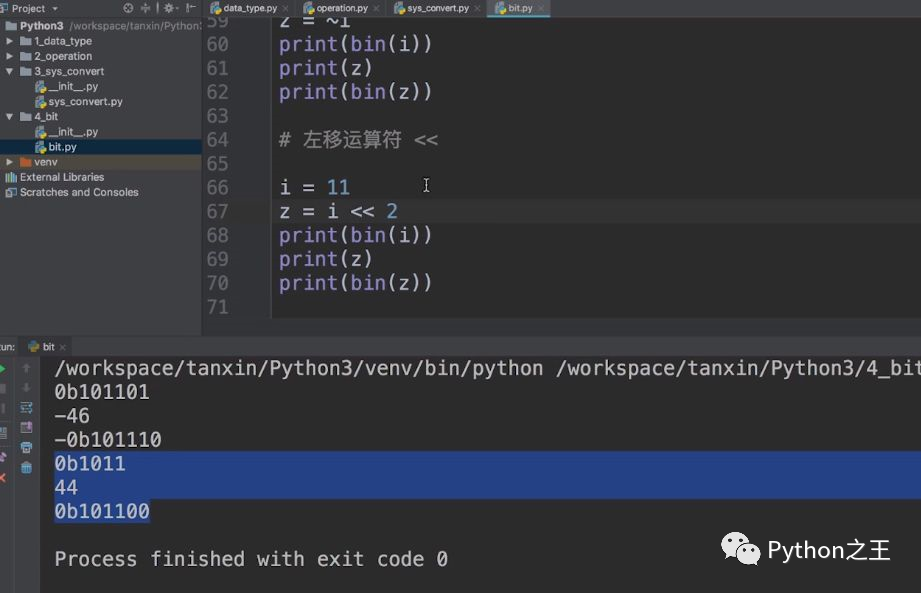
这个结果44到底是怎么样来进行运算的?左移2位,就是1011往左移动2位,然后用0来补充,变成了101100。本来在这里向左边移动,其实是后边舍弃掉2位
1011
----
101
所以,1011的右移2位的运算就是101100,然后将二进制的101100转化为十进制,就是我们的结果44。
右移运算符
下面,我们介绍右移运算符。右移运算符是:>>。我们计算11的右移2位的运算,得到的结果是2。
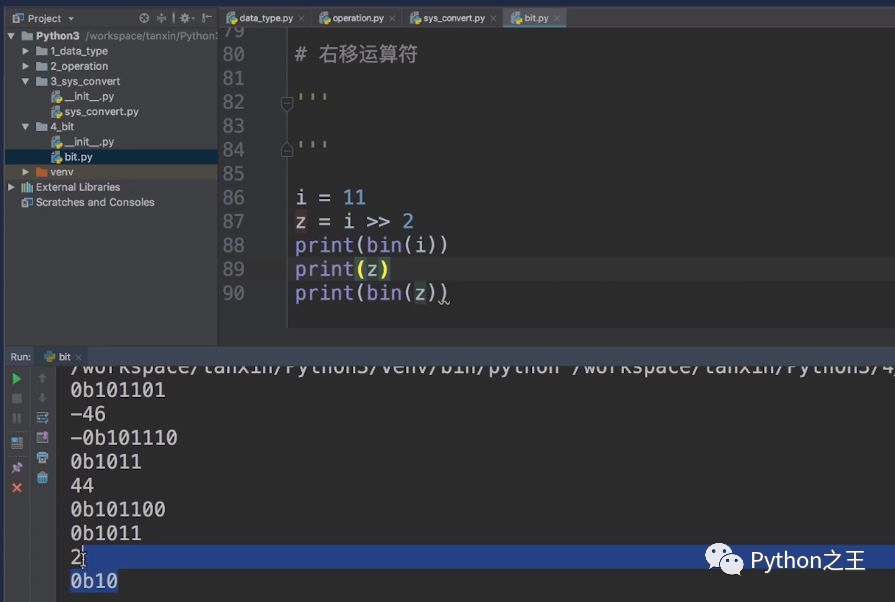
这个结果2到底是怎么样来进行运算的?右移2位,就是1011往右移动2位,然后右边的11直接去除,变成了10。本来在这里向右边移动,其实是后边删除位数。
1011
----
10
所以,1011和的左移2位的运算就是10,然后将二进制的10转化为十进制,就是我们的结果2。下表就是总结。
| 符号 | 意义 | 示例 |
|---|---|---|
| ~ | 逻辑非运算 | ~a |
| & | 逻辑与运算 | a&b |
| | | 逻辑或运算 | a|b |
| << | 位左移运算 | a<<2 |
| >> | 位右移运算 | a>>2 |
判断奇数还是偶数
通常判断奇数还是偶数我们想到的办法就是除以2,看余数是否为0。具体Python代码如下:
def isodd(x):
return True if (x % 2 == 0) else False
那么如何使用位运算呢?
我们只需要使用&运算,与1进行&,如果为1,那么该数为奇数;如果为0,那么该数是偶数,具体Python代码如下:
def isodd(x):
return True if (x & 1) else False
左移一位相当于乘以2,右移一位相当于除以2
在面试的过程中,通常会遇到的一个问题是写二分查找代码。
Python二分查找的代码如下:
def binary_search(list, item):
'''
:param list: 有序列表
:param item: 要查找的元素
:return: item在list中的索引,若不在list中返回None
'''
low = 0
high = len(list) - 1
while low <= high:
mid = (low + high) // 2
if list[mid] == item:
return mid
elif list[mid] < item:
low = mid + 1
elif list[mid] > item:
high = mid - 1
return None
其中有一步是需要取最小下标和最大下标的中间值,若使用位运算符,则变成midpoint = (low + high) >> 1,面试官肯定会对你刮目相看。
下面就是位运算常见用法总结
「判断x的奇偶数」
x % 2 == 1 // 常规写法
x & 1 == 1 // 为真奇数,为假偶数
「计算中位数」
mid = (left + right) / 2 // 常规写法
mid = (left + right) >> 1 // 位运算
LeetCode 第 78题:子集
下面,我们来看一题关于二进制的Leetcode。题目很简单,就是给定一组不含重复元素的整数数组 nums,返回该数组所有可能的子集(幂集)
#给定一组不含重复元素的整数数组 nums,返回该数组所有可能的子集(幂集)。
# 说明:解集不能包含重复的子集。
# 示例:
# 输入: nums = [1,2,3]
#输出:
#[
# [3],
# [1],
# [2],
# [1,2,3],
# [1,3],
# [2,3],
# [1,2],
# []
#]
# Related Topics 位运算 数组 回溯算法
既然这道题让我们求的是所有的子集,那么我们可以从子集的特点入手。假如整数数组的长度是3,那么子集有8个。整数数组的长度是4,那么子集有16个。
一个含有n个元素的子集的数量是,这个是高中数学中的集合的数学题,不知道的可能忘得一干二净。
这题非常巧妙地使用二进制的位运算。使用位运算,对每一位为1的表示这一位的数字存在,求[1,2,3] 的子集,我们可以用0和1表示有和无。比如编码001,表示只含有3,编码101,表示含有1,3。编码111表示1,2,3。
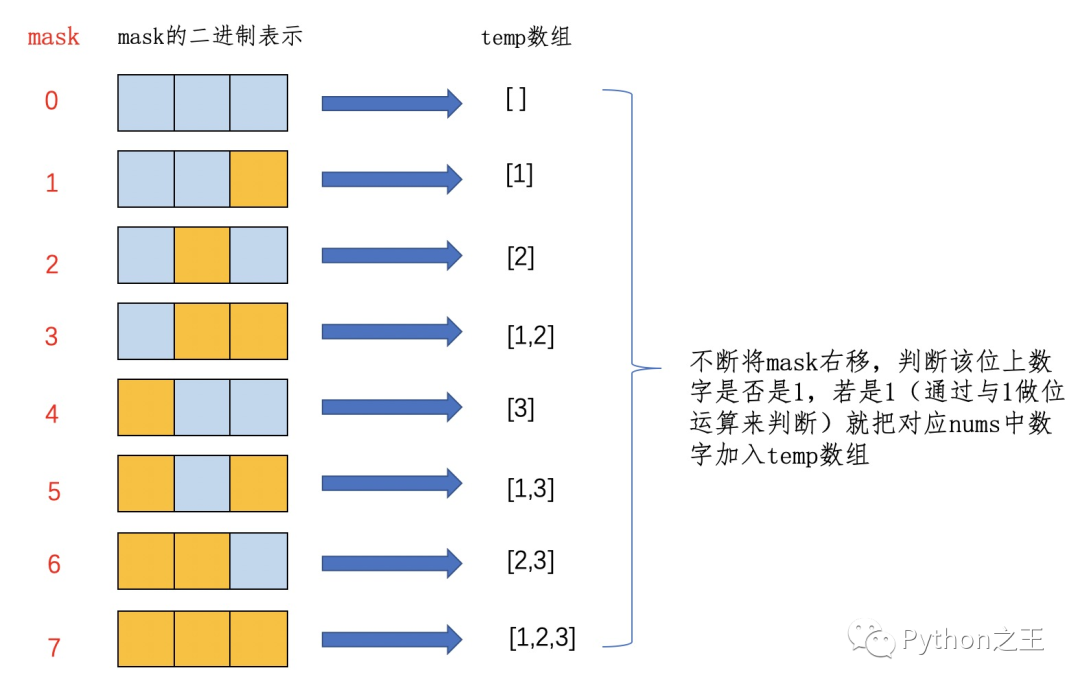
因为每个数只有选与不选两种情况,具体的情况如下所示。
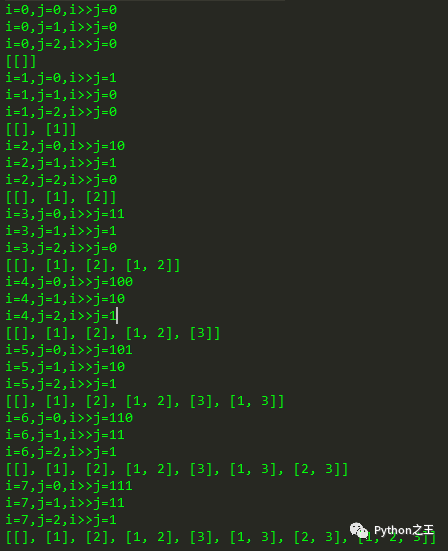
具体的Python代码。
class Solution:
def subsets(self, nums: List[int]) -> List[List[int]]:
ret = []
n = len(nums)
# 遍历所有的状态
# 二进制的巧用:1左移n位相当于2的n次方,也可以写成2**n
for s in range(1 << n):
cur = []
# 通过位运算找到每一位是0还是1
for i in range(n):
# 判断s状态在2的i次方上,也就是第i位上是0还是1
if s & (1 << i):
cur.append(nums[i])
ret.append(cur[:])
return ret
其实位运算说简单,也很简单,但有的时候要用,我却怎么也想不到,主要是因为奇葩很多。
在此题中,还有一种方法是回溯算法,注意需要将空集的情况添加。
class Solution:
def subsets(self, nums: List[int]) -> List[List[int]]:
res = [[]]
for i in nums:
res = res + [[i] + num for num in res]
return res
❝本文已收录 GitHub,传送门~[1] ,里面更有大厂面试完整考点,欢迎 Star。
❞
Reference
传送门~: https://github.com/MaoliRUNsen/runsenlearnpy100
更多的文章
点击下面小程序
- END -

