真实世界的异或运算

对于底层开发来说，位运算是非常重要的一类操作。而对于位运算来说，最有意思的，应该就是异或运算（XOR）了。

提到异或运算，很多同学可能首先想到的就是一个经典的，和异或运算相关的面试问题：

给你一个包含有 n - 1 个元素的数组，其中每个数字在 [1, n] 的范围内，且不重复。也就是从 1 到 n 这 n 个数字，有一个数字没有出现在这个数组中。编写一个算法，找到这个丢失的数字。

诚然，这样的问题可以考察大家是否真正理解异或运算，但其实这种问题没什么意义。

是的，可能大家发现了，作为一个喜欢算法，经常玩儿算法，每天在慕课网的课程问答区回答大家算法问题的老师，我却经常怼各种算法问题没有什么意义... 

因为我们在实际编程中，很难遇到这样的场景：有一个数组，有 n - 1 个元素，其中恰好其中一个元素丢失了...

但在这篇文章中，你将看到，真实世界的异或运算是被怎样应用的。

1.

为了文章的完整性，我们先简单来看一下，什么是异或运算？

非常简单：相同为 0，不同为 1。

大多数编程语言使用符号 ^ 来表示异或运算。

如果我们使用真值表来表示的话，异或运算是这样的：

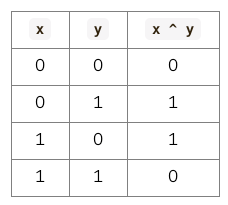
在这里，大家可以仔细体会一下，什么叫相同为 0；不同为 1。

异或运算真值表的第 1 行和第 4 行在说：相同为 0。

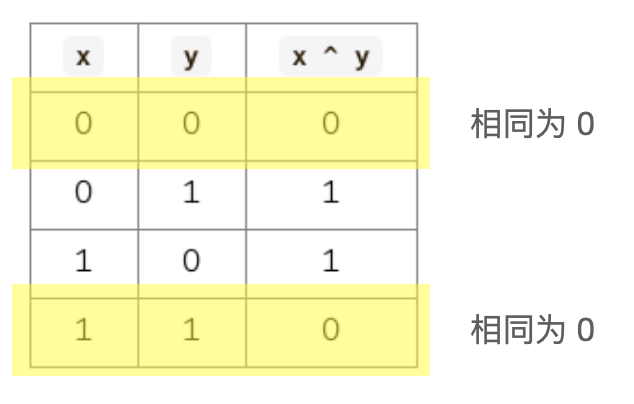
异或运算真值表的第 2 行和第 3 行在说：不同为 1。

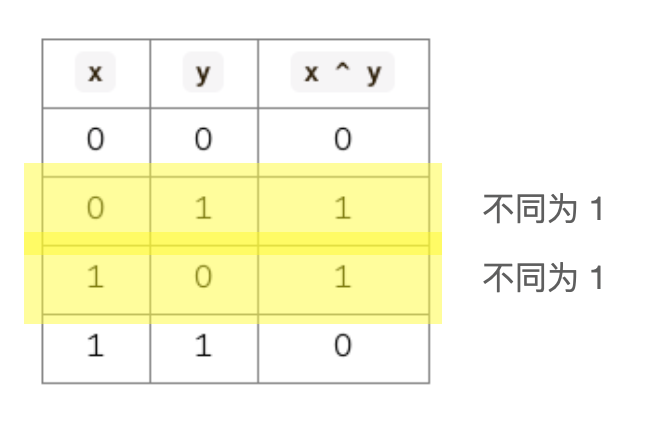
相同为 0，是异或运算的最重要的性质之一。即：

x ^ x = 0

而异或运算最重要的性质之二，可以通过这个真值表的前两行看出来。就是 0 和任何一个数字（y）异或的结果，都是这个数字本身。即：

0 ^ y = y

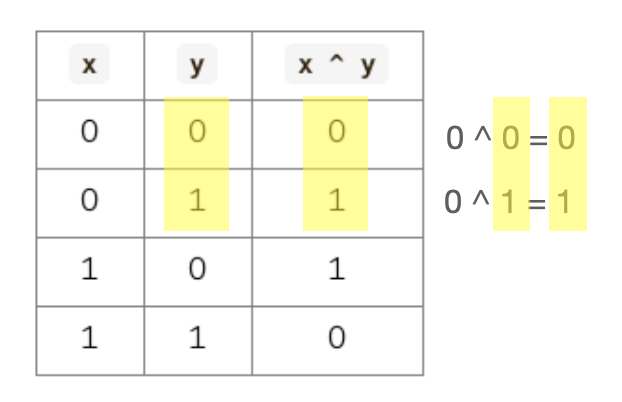
当然，我们通过这个真值表，可以很轻易看出来，异或运算满足交换律，即：

x ^ y = y ^ x

所以，上面的性质，我们也可以说成是：任意一个数字(x)，和 0 异或的结果，还是这个数字本身。即：

x ^ 0 = x

好了，了解了异或运算的这些性质，我们就已经完全可以理解绝大多数异或的应用了。

2.

在具体看异或逻辑更加实际的应用之前，我们还是先来简单分析一下文章开始，那个经典的面试问题，来做一做热身。

给你一个包含有 n - 1 个元素的数组，其中每个数字在 [1, n] 的范围内，且不重复。也就是从 1 到 n 这 n 个数字，有一个数字没有出现在这个数组中。编写一个算法，找到这个丢失的数字。

如果使用异或解决的话，只需要首先计算出从 1 到 n 这 n 个数字的异或值，然后，再将数组中的所有元素依次和这个值做异或，最终得到的结果，就是这个丢失的数字。

写成式子就是：

1 ^ 2 ^ 3 ^ ... ^ n ^ A[0] ^ A[1] ^ A[2] ^ ... ^ A[n - 2]

这个算法为什么是正确的？

因为在这个式子中，除了丢失的那个数字只出现了一次，其他数字都出现了两次。

所以，两个相同的数字做异或，结果为 0；最终只出现一次的那个数字，和 0 做异或，结果就是这个丢失的数字。

值得一提的是，对于这个问题，我们完全可以不使用异或运算，也设计出一个时间复杂度是 O(n)，空间复杂度是 O(1) 的算法。方法是，先计算出 1 到 n 的和，再用这个和，依次减去数组中的数字就好了。

而 1 到 n 的和，可以通过等差数列求和公式直接计算出：

(1 + n) * n / 2 - A[0] - A[1] - A[2] - ... - A[n - 2]

但是，这个方法有一个问题，就是如果 n 比较大的话，1 到 n 的数字和会超出整型范围，导致整型溢出。

实际上，当 n 到达 7 万这个规模的时候，1 到 n 的数字和就已经不能使用 32 位 int 表示了。当然，我们可以使用 long 来表示，但使用 long 做运算，性能是比使用 int 慢的。

使用异或，则完全没有这个问题。

这个经典的面试问题，可以很容易地被改变成如下版本：

多余的数：给你一个包含有 n + 1 个元素的数组，其中每个数字在 [1, n] 的范围内，且 1 到 n 每个数字都会出现。也就是从 1 到 n 这 n 个数字，有一个数字在这个数组中出现了两次。编写一个算法，找到这个多余的数字。

相信理解了上面的问题，这个问题就很简单了。答案是首先计算出从 1 到 n 这 n 个数字的异或值，然后，再将数组中的所有元素依次和这个值做异或，最终得到的结果，就是这个多余的数字。

是的，算法一模一样。只不过现在，第二部分有 n + 1 个元素，而非 n - 1 个元素而已：

1 ^ 2 ^ 3 ^ ... ^ n ^ A[0] ^ A[1] ^ A[2] ^ ... ^ A[n]

这个算法为什么是正确的？

因为在这个式子中，除了多余的那个数字出现了三次，其他数字都出现了两次。所以，其他数字通过异或，结果都为 0，而一个数字和自己做 3 次异或运算，结果还是它自己：

x ^ x ^ x = 0 ^ x = x

据此，我们可以非常简单地得到结论：

一个数字和自己做偶数次异或运算，结果为 0；

一个数字和自己做奇数次异或运算，结果为 1。

3.

异或运算最典型的一个应用，是做两个数字的交换。

传统的两个数字的交换，是使用这样的三个赋值语句：

int t;x = t;x = y;y = t;

这样做的问题是，需要一个额外的临时变量 t。为一个新的变量开空间，是性能的损耗，哪怕这只是一个 int 值而已。这一点，在高级编程语言中体现不出来，但是在底层开发中，就会有影响。

而我们使用异或运算，完全可以不使用这个额外的临时变量。只需要这样就好：

x ^= y;y ^= x;x ^= y;

为了理解这个过程为什么是正确的，我们可以画如下的示意图：

初始的时候，x 里就是 x；y 里就是 y：

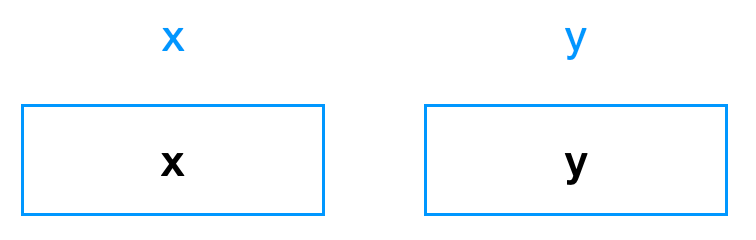
第一句话 x^=y，实际上，让 x 里放的是 x ^ y：

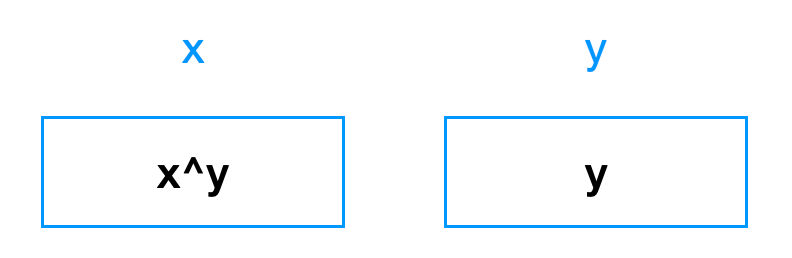
第二句话 y^=x，实际上，让 y 和当下 x 里存放的值：x ^ y 进行了异或：

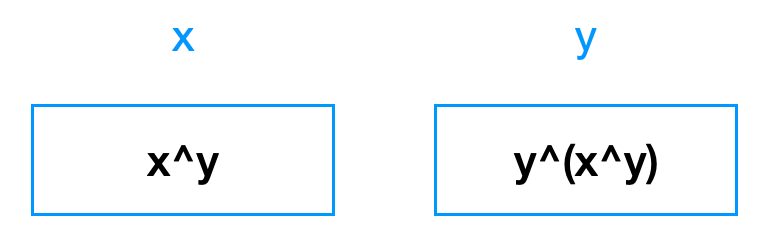
注意，此时，y 里有一个 x 和两个 y 。两个 y 异或的结果就是 0，所以，此时 y 里存放的是 x：

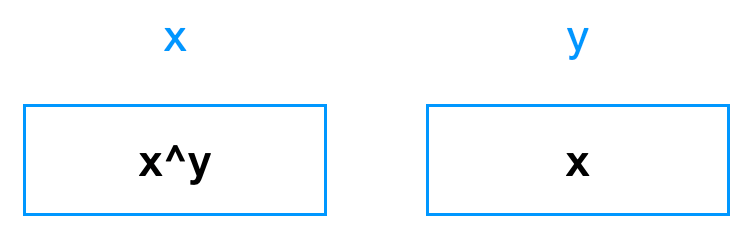
最后，第三句话，再一次 x ^= y，但因为现在 x 里存放的是 x^y，y 里存放的是 x，所以，这句话以后，x 中是 (x^y)^x：

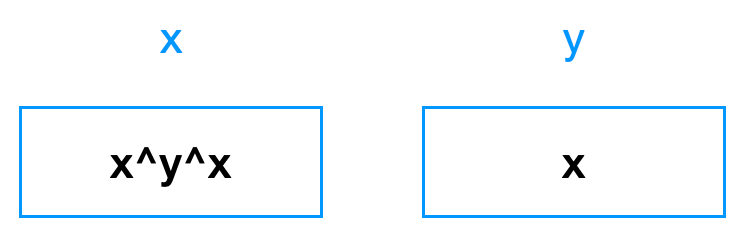
此时，x 里有两个 x 和一个 y 。两个 x 异或的结果就是 0。所以此时，x 里存放的是 y 的值：

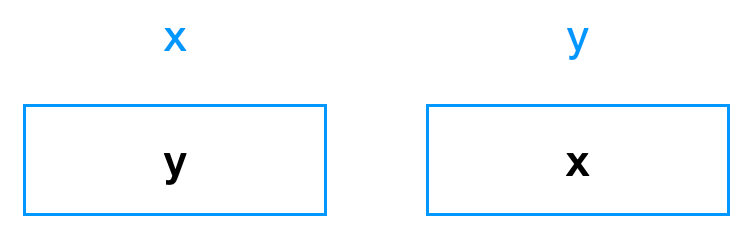
至此，x 和 y 的交换完成了。

4.

大多数资料关于使用异或运算进行两个数字的交换，介绍到此，就结束了。而实际上，这个算法是有 bug 的。

这个 bug 在 2005 年，第一次被 Iain A. Fleming 发现。

在上面的演示中，如果 x 和 y 是两个不同的地址，才成立。

但如果 x 和 y 是同一个地址呢？比如，我们调用的是 swap(A[i], A[j])，其中 i == j。此时，上面的算法是错误的。

因为，在这种情况下，我们第一步做的 x ^= y，实际上就是 A[i] ^= A[i]。这将直接让 A[i] 中的元素等于 0，而丢失原本存在 A[i] 中的元素。后续，这个元素就再也找不回来了。

针对这个 bug，解决方案是，在做这个交换之前，判断一下 x 和 y 的地址是否相同。

由于在一些语言中，拿到变量的地址并不容易（甚至没有这个能力），所以，可以把逻辑改变为，判断一下 x 和 y 是否相同。如果相同，则什么都不做。

因为如果 x 和 y 的地址一样，x 和 y 的值肯定也一样，什么都不做，则避免了这个 bug；

即便 x 和 y 的地址不一样，但如果 x 和 y 的值相同，什么都不做也是正确的。

所以，我们的逻辑变成了这样：

if(x != y){        x ^= y;        y ^= x;        x ^= y;}

因为在底层编程中，if 判断也是比较耗费性能的，所以，一个更优雅的写法是这样的（C / C++）：

(x == y) || ((x ^= y), (y ^= x), (x ^= y))

在这个写法中，巧妙地使用了逻辑短路，如果第一个表达式 x == y 成立，后面的交换过程就不会被执行了；否则，运行后面的交换逻辑。

这样写，整个逻辑中没有了 if 判断。

在极端情况下，即使在高级语言编程中，没有 if 运算也将大大提升程序性能。可以参考我之前的文章：用简单的代码，看懂 CPU 背后的重要机制

值得一提的是，2009 年，Hallvard Furuseth 提出，下面的写法性能更优，因为表达式 x^y 可以被缓存重复利用：

(x ^ y) && (y ^= x ^= y, x ^= y)

在 2007 年和 2008 年，Sanjeev Sivasankaran 和 Vincent Lefèvre 提出，这个交换过程也可以使用加减运算完成：

(&a == &b) || ((a -= b), (b += a), (a = b - a))

篇幅原因，在这里，我就不对这个逻辑做模拟了。感兴趣的同学，可以使用文章中的方法，自行模拟，验证这个算法的正确性：）

5.

异或运算的另一个直接应用，是编译器的优化，或者是 CPU 底层的优化。

举个简单的例子，在很多编译器的内部，判断 if(x != y)

本质是在判断：if((x ^ y) != 0)

很多同学可能会从数学的角度，认为判断 x 是否等于 y，是看 x - y 的结果是否为 0。

但实际上，减法是一个比异或操作复杂得多的操作。如果学习过数字电路的同学会知道，设计一个减法器，并不容易。

但是，两个数字按位异或，就非常容易了。

另一方面，在计算机底层，异或的一个重要的应用，是清零。

因为自己和自己异或的结果是零，所以，近乎所有的 CPU 指令中，清零操作都是使用异或完成的。

xor same, same

还记得之前说的，两个元素交换的 bug 吗？这个 bug 的本质，就是当两个元素的地址一样的时候，相当于对这个地址做清零了。

当然，从体系结构的角度，这个清零不仅仅可以发生在内存，也可以发生在寄存器。

xor reg, reg

对于这个问题，在 stackoverflow 上有一个非常好的讨论。感兴趣的同学可以阅读一下：

https://stackoverflow.com/questions/33666617/what-is-the-best-way-to-set-a-register-to-zero-in-x86-assembly-xor-mov-or-and

What is the best way to set a register to zero in x86 assembly: xor, mov or and?

6.

真正让异或运算大获异彩的，其实是在密码学领域，尤其是在对称加密领域。

实际上，异或运算近乎被应用在了所有的对称加密算法中。

系统地讲解密码学已经远超这篇文章的范畴了。在这里，我只给出一个简单的例子，让大家可以直观地理解，为什么异或运算可以用在对称加密算法中。

比如说，我们有一个密文。这个密文就是 hi 吧。它所对应的二进制是：

01101000 01101001

下面，我们可以生成一个秘钥。为了简单起见，我们假设生成的秘钥和密文是等长度的。比如密钥是 66，对应的二进制是这样的：

00110110 00110110

那么，我们将密文和秘钥做异或操作，得到的结果，就是加密后的信息：

01101000 01101001 (密文)异或00110110 00110110 (秘钥)=01011110 01011111 (加密信息)

这个加密信息，对应的字符串是 ^_

这个字符串显然没有意义。但是，如果你知道秘钥 66 的话，将这个加密信息和秘钥 66 再做异或运算，就可以恢复原先的密文 hi。

相信看到这里，这背后的原理，大家都已经了解了。是异或运算性质最基本的应用，其实非常简单。

当然，生产环境的对称加密没有这么简单，但这是最基础的原理。

如果有兴趣的同学，可以搜索学习一下 DES（Data Encryption Standard） 和 AES（Advanced Encryption Standard），就会看到异或运算在其中所起的重要作用。

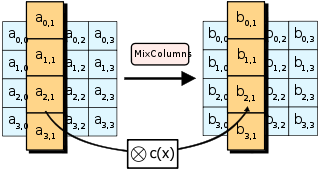
实际上，在编码学领域，特别是各类纠错码和校验码，异或运算也经常出现。

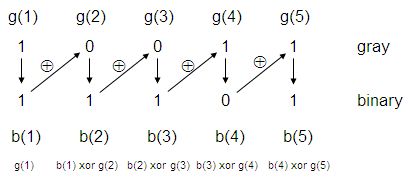
比如奇偶校验，比如 CRC 校验，比如 MD5 或者 SHA256，比如 Hadamard 编码或者 Gray 码（格雷码）。

格雷码可能很多同学都听说过，一般在离散数学或者组合数学中会接触。

最近力扣有一次周赛的问题，本质其实是格雷码和对应二进制数字之间的转换，有兴趣的同学可以了解一下：

如果明白格雷码的原理，这个 Hard 问题就是 Easy 问题，一通异或运算就解决了 

7.

最后，说一个我最喜欢的异或的应用。

使用异或，可以编写更加节省空间的双向链表，被称为是异或双向链表（XOR linked list）。

在维基百科中，专门收录了这个词条：

这种双向链表，由 Prokash Sinha 在 2004 年第一次提出，并且发表在了 Linux Journal 上。被称为是：A Memory-Efficient Doubly Linked List（一种更有效利用空间的双向链表）。

感兴趣的同学，可以在这里阅读这篇文章：

https://www.linuxjournal.com/article/6828

在原文中，作者对相关的数据结构进行了代码级别的定义。

实际上，这种数据结构的原理非常简单。

在通常的双向链表中，每一个节点需要有两个指针，一个 prev，指向之前的节点；一个 next，指向之后的节点。

但是，异或双向链表中，只有一个指针，我们可以管它叫 xor_ptr。这个指针指向的地址，是 prev 和 next 两个地址异或的结果。其中，头结点的 prev 地址取 0；尾结点的 next 地址取 0。

这样一来，如果我们需要获得一个节点的 next 的地址，只需要 xor_ptr ^ prev 就好；

如果我们需要获得一个节点的 prev 的地址，只需要 xor_ptr ^ next 就好。

我们之所以可以这么做，是因为对于双向链表，所有的查询操作，肯定是从头到尾，或者从尾到头进行的，而不可能直接从中间进行。也就是所谓的链表不支持随机访问。

因此，在我们遍历异或双向链表的过程中，如果我们是从头到尾遍历的话，我们就可以一直跟踪每一个节点的 prev  值。用这个值和 xor_ptr 做异或操作，拿到每一个节点的 next；

同理，如果我们是从尾到头遍历的话，我们就可以一直跟踪每一个节点的 next 值。用这个值和 xor_ptr 做异或操作，就可以拿到每一个节点的 prev 。

我强烈建议感兴趣的同学，自己动手编程实现一个异或双向链表，是一个很有意思，也很酷的编程练习：）

8.

文章的最后，聊一个我第一次接触异或运算，产生的疑问，相信很多同学都有。

那就是，异或运算，为什么叫异或？这个名称命名的来源，显然和或运算（or）有一些关系，但是这个关系到底是什么？

答案是，异或运算可以表示成这样：

x ^ y = (!x and y)  or (x and !y)

右边的式子也很好理解。因为异或运算就是 x 和 y 不同为真。

所以，!x and y 表示 x 和 y 不同，其中 x 为 0，y 为 1；

x and !y 也表示 x 和 y 不同，其中 x 为 1，y 为 0；

这两种情况的任何一个，在异或的定义下，都是真。所以，这两种情况，是或的关系。

看，异或这个概念就被这样对应起来了：

异，就是 x 和 y 不同；或，就是这两种情况取或的关系。

是不是很酷？

大家加油！：）