(附代码)实战 | 变分自编码器的原理与项目
 目录
目录12.4.1 概述
12.4.2 基本原理
2.1 Encoder
2.2 Decoder
2.3 Self-Attention
2.4 Multi-Headed Attention
2.5 Positional Encoding
12.4.3 应用任务和结果
3.1 NLP领域
3.2 CV领域
3.2.1 检测DETR
3.2.2 分类ViT
3.2.3 分割SETR
3.2.4 Deformable-DETR
12.4.4 优点及分析
12.4.5 缺点及分析
参考文献
1 概述
VAE 可以从神经网络的角度或者概率图模型的角度来解释。
理解变分自编码器的基本原理只需要关注整个模型的三个关键元素:
编码网络(Encoder Network),也称 推断网络 。该 NN 用来生成隐变量的参数(隐变量由多个高斯分布组成)。对于隐变量 z zz ,首先初始化时可以是标准高斯分布,然后通过这个 NN,通过不断计算后验概率 q ( z ∣ x ) q(z|x)q(z∣x) 来逐步确定高斯分布的参数(均值和方差)。
隐变量(Latent Variable)。作为 Encoder 过程的产物,隐变量至少能够包含一些输入数据的信息(降维的作用),同时也应该具有生成类似数据的潜力。
解码网络(Decoder Network),也称 生成网络。该 NN 用于根据隐变量生成数据,我们希望它既有能力还原 encoder 的数据,同时还能根据数据特征生成一些输入样本中不包含的数据。
2 基本原理
1. 定义
VAE 全名叫 变分自编码器,是从之前的 auto-encoder 演变过来的,auto-encoder 也就是自编码器,自编码器,顾名思义,就是可以自己对自己进行编码,重构。所以 AE 模型一般都由两部分的网络构成,一部分称为 encoder, 从一个高维的输入映射到一个低维的隐变量上,另外一部分称为 decoder, 从低维的隐变量再映射回高维的输入:
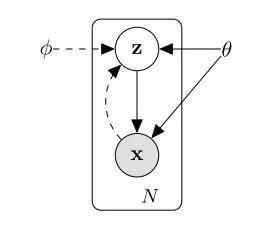
(a) VAE模型
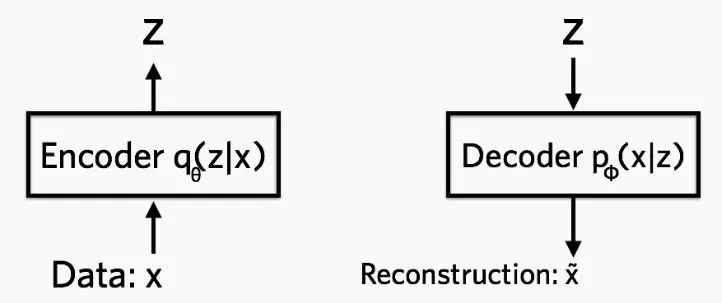
(b) 编码与重构
图1 VAE模型

2. 理论基础:三要素
隐变量(Latent Variable)。上面已经讲过隐变量的基本概念,这里介绍隐变量在 VAE模型中的作用及特点。
隐变量 z 是可以认为是隐藏层数据,它是不限定数目的符合 高斯分布 特征的数据。(根据实际情况确定数目)
z 由输入数据 X 的采样以及参数生成,它既包含 X 的信息(这个于 AutoEncoder 的隐藏层类似),同时也满足 高斯分布,方便接下来进行梯度下降或者其他优化技术 [1]。
隐变量的作用除了让生成网络尽可能还原原来的数据 X ,同时也能生成原来数据中不存在的数据。
首先当我们引入隐变量 z 以后,可以用 z 来表示 P(x) :
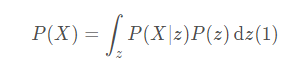
其中,用 P(X|z) 替代了 f(z),这样可以用概率公式明确表示 X 对 Z 的依赖性;P(z) 即高斯分布;其中 μN((z),σ(z)),其中的均值μ(z) 和 方差 σ(z) 需要通过运算获得。
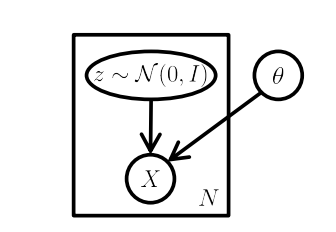
图2 VAE模型的一个图模型
如图所示,标准的VAE模型是一个图模型,注意明显缺乏任何结构,甚至没有 “编码器” 路径:可以在不输入的情况下从模型中采样。这里,矩形是 “板符号”,这意味着我们可以在模型参数 θ 保持不变的情况下,从 z 和 X 中采样N次。
Step 2 - Decoder 过程
上面也曾讲过,VAE 模型中同样有 Encoder 与 Decoder 过程,也就是说模型对于相同的输入时,也应该有尽可能相同的输出。所以这里再次遇到 Maximum likelihood(极大似然)。
在公式 (1) 中,将 P(X)用 Z 来表示,所以对任何输入数据,应该尽量保证最后由隐变量而转换回输出数据与输入数据尽可能相等。
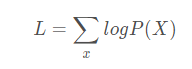
式(2)
为了让公式 2 的输出极大似然 X ,神经网络登场,它的作用就是调参,来达到极大似然的目的。(注意这里虽然介绍在前,但其实在训练的时候与后面的 NN 是同时开始训练)
本步介绍的是如何实现与 AE 类似的功能,即保证输出数据极大似然与输入数据。
这里用到的网络称为 VAE 中的 生成网络,即根据隐变量 Z 生成输出数据的网络。


全书链接:https://github.com/Charmve/computer-vision-in-action

图5 最大似然估计推导

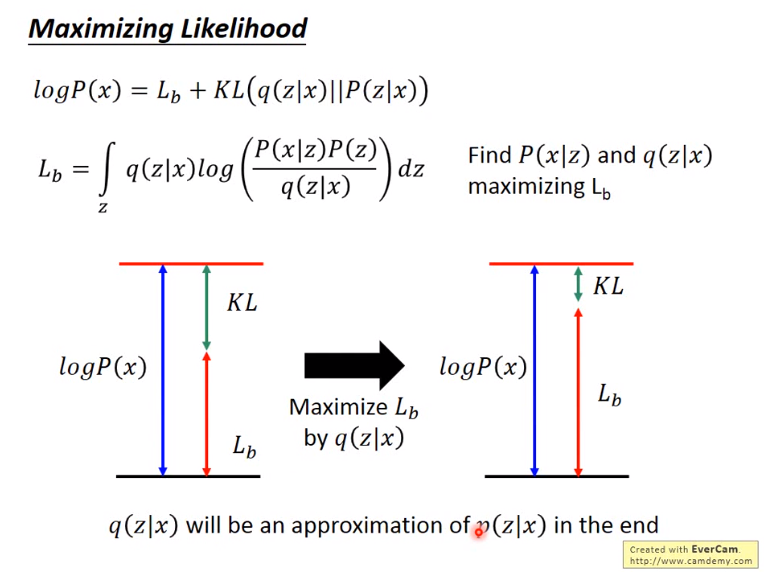
图6 最大似然概率估计

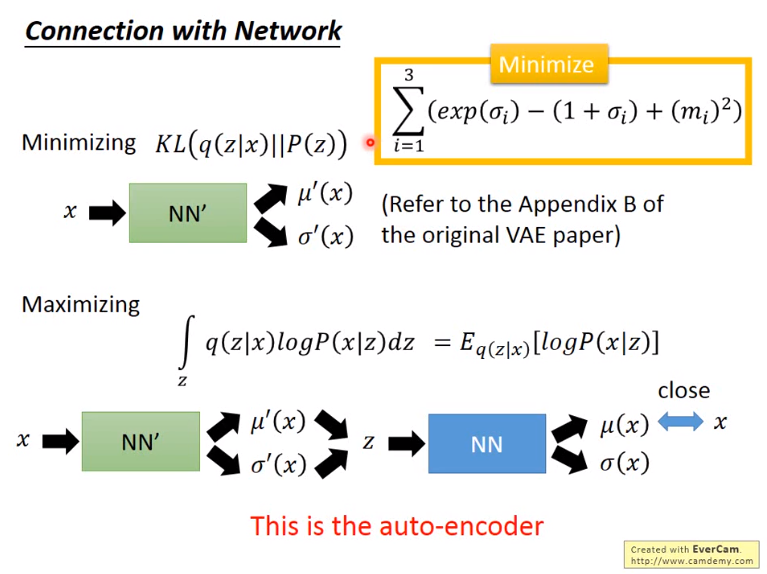
图8 与NN连接

本文来自于GitHub《计算机视觉实战演练:算法与应用》,全书请参考原文。
链接:https://github.com/Charmve/computer-vision-in-action
3 VAE v.s. AE 区别与联系
(1)区别
VAE 中隐藏层服从高斯分布,AE 中的隐藏层无分布要求
训练时,AE 训练得到 Encoder 和 Decoder 模型,而 VAE 除了得到这两个模型,还获得了隐藏层的分布模型(即高斯分布的均值与方差)
AE 只能重构输入数据X,而 VAE 可以生成含有输入数据某些特征与参数的新数据。
(2)联系
VAE 与 AE 完全不同,但是从结构上看都含有 Decoder 和 Encoder 过程。
4 变分自编码器的代码实现
如果只是基于 MLP 的VAE,就是普通的全连接网络:
import tensorflow as tffrom tensorflow.contrib import layers## encoder 模块def fc_encoder(x, latent_dim, activation=None):e = layers.fully_connected(x, 500, scope='fc-01')e = layers.fully_connected(e, 200, scope='fc-02')output = layers.fully_connected(e, 2 * latent_dim, activation_fn=activation,scope='fc-final')return output## decoder 模块def fc_decoder(z, observation_dim, activation=tf.sigmoid):x = layers.fully_connected(z, 200, scope='fc-01')x = layers.fully_connected(x, 500, scope='fc-02')output = layers.fully_connected(x, observation_dim, activation_fn=activation,scope='fc-final')return output
关于这几个 loss 的计算:
## KL lossdef _kl_diagnormal_stdnormal(mu, log_var):var = tf.exp(log_var)kl = 0.5 * tf.reduce_sum(tf.square(mu) + var - 1. - log_var)return kl## 基于高斯分布的重建lossdef gaussian_log_likelihood(targets, mean, std):se = 0.5 * tf.reduce_sum(tf.square(targets - mean)) / (2*tf.square(std)) + tf.log(std)return se## 基于伯努利分布的重建lossdef bernoulli_log_likelihood(targets, outputs, eps=1e-8):log_like = -tf.reduce_sum(targets * tf.log(outputs + eps)+ (1. - targets) * tf.log((1. - outputs) + eps))return log_like

全书链接:https://github.com/Charmve/computer-vision-in-action
5 卷积变分自编码器的实现与简单应用
本次实验采用的是 notebook,可以是自己电脑上安装的 jupyter notebook,也可以使用自己云服务器安装的,也可以考虑使用谷歌提供的 Colaboratory。
文件地址:/notebooks/16_CVAE.ipynb
1. 安装依赖
确定使用的是 tensorflow 2.x
!pip show tensorflow如果当前安装的不是 tensorflow 2.x 的话,请输入以下命令安装:
!pip install tensorflow==2.3.0 -i https://pypi.tuna.tsinghua.edu.cn/simple安装 imageio
!pip install imageio2. 导入相关库与加载数据集
import tensorflow as tfimport osimport timeimport numpy as npimport globimport matplotlib.pyplot as pltimport PILimport imageiofrom IPython import display_), (test_images, _) = tf.keras.datasets.mnist.load_data()train_images = train_images.reshape(train_images.shape[0], 28, 28, 1).astype('float32')test_images = test_images.reshape(test_images.shape[0], 28, 28, 1).astype('float32')# 标准化图片到区间 [0., 1.] 内train_images /= 255.test_images /= 255.# 二值化>= .5] = 1.< .5] = 0.>= .5] = 1.< .5] = 0.# 使用 tf.data 来将数据分批和打乱train_dataset = tf.data.Dataset.from_tensor_slices(train_images).shuffle(TRAIN_BUF).batch(BATCH_SIZE)test_dataset = tf.data.Dataset.from_tensor_slices(test_images).shuffle(TEST_BUF).batch(BATCH_SIZE)
3. VAE 模型
准备工作做完了后,这里正式开始编写实现VAE模型。
(1) 重参数化技巧 (Reparameterization Trick)
训练过程中,为了生成样本 z 以便于 decoder 操作,我们可以从 encoder 生成的分布中进行采样。但是,由于反向传播无法通过随机节点,因此此采样操作会产生瓶颈。
为了解决这个问题,我们使用了一个重新参数化的技巧。我们使用 decoder 参数和另一个参数 ε \varepsilonε 近似z,如下所示:
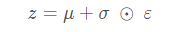
式(12)
其中 μ 和 σ表示高斯分布中的 均值 和 标准差。它们可以从 decoder 输出中导出。可以认为 ε 是用来保持 z 随机性的随机噪声。我们从标准正态分布生成。
现在的 z 是 q(z∣x) 生成(通过参数 μ,σ 和 ε),这将使模型分别通过 μ, σ 在 encoder 中 反向传播梯度,同时通过 ε 保持 z 的随机性。
(2) 网络结构 (Network architecture)
对于 VAE 模型构建,
在 Encoder NN中,使用两个卷积层和一个完全连接的层。、
在 Decoder NN中,通过使用一个完全连接的层和三个卷积转置层来镜像这种结构。
注意,在训练VAE时,通常避免使用批次标准化,因为使用小批量的额外随机性可能会加剧抽样随机性之外的不稳定性。
class CVAE(tf.keras.Model):"""Convolutional variational autoencoder."""def __init__(self, latent_dim):super(CVAE, self).__init__()self.latent_dim = latent_dimself.encoder = tf.keras.Sequential([tf.keras.layers.InputLayer(input_shape=(28, 28, 1)),tf.keras.layers.Conv2D(filters=32, kernel_size=3, strides=(2, 2), activation='relu'),tf.keras.layers.Conv2D(filters=64, kernel_size=3, strides=(2, 2), activation='relu'),tf.keras.layers.Flatten(),# No activationtf.keras.layers.Dense(latent_dim + latent_dim),])self.decoder = tf.keras.Sequential([tf.keras.layers.InputLayer(input_shape=(latent_dim,)),tf.keras.layers.Dense(units=7*7*32, activation=tf.nn.relu),tf.keras.layers.Reshape(target_shape=(7, 7, 32)),tf.keras.layers.Conv2DTranspose(filters=64, kernel_size=3, strides=2, padding='same',activation='relu'),tf.keras.layers.Conv2DTranspose(filters=32, kernel_size=3, strides=2, padding='same',activation='relu'),# No activationtf.keras.layers.Conv2DTranspose(filters=1, kernel_size=3, strides=1, padding='same'),])@tf.functiondef sample(self, eps=None):if eps is None:eps = tf.random.normal(shape=(100, self.latent_dim))return self.decode(eps, apply_sigmoid=True)def encode(self, x):mean, logvar = tf.split(self.encoder(x), num_or_size_splits=2, axis=1)return mean, logvardef reparameterize(self, mean, logvar):eps = tf.random.normal(shape=mean.shape)return eps * tf.exp(logvar * .5) + meandef decode(self, z, apply_sigmoid=False):logits = self.decoder(z)if apply_sigmoid:probs = tf.sigmoid(logits)return probsreturn logits
4. 定义损失函数和优化器

optimizer = tf.keras.optimizers.Adam(1e-4)def log_normal_pdf(sample, mean, logvar, raxis=1):log2pi = tf.math.log(2. * np.pi)return tf.reduce_sum(-.5 * ((sample - mean) ** 2. * tf.exp(-logvar) + logvar + log2pi),axis=raxis)def compute_loss(model, x):mean, logvar = model.encode(x)z = model.reparameterize(mean, logvar)x_logit = model.decode(z)cross_ent = tf.nn.sigmoid_cross_entropy_with_logits(logits=x_logit, labels=x)logpx_z = -tf.reduce_sum(cross_ent, axis=[1, 2, 3])logpz = log_normal_pdf(z, 0., 0.)logqz_x = log_normal_pdf(z, mean, logvar)return -tf.reduce_mean(logpx_z + logpz - logqz_x)def train_step(model, x, optimizer):"""Executes one training step and returns the loss.This function computes the loss and gradients, and uses the latter toupdate the model's parameters."""with tf.GradientTape() as tape:loss = compute_loss(model, x)gradients = tape.gradient(loss, model.trainable_variables)optimizer.apply_gradients(zip(gradients, model.trainable_variables))
全书链接:https://github.com/Charmve/computer-vision-in-action
5. 训练模型与生成图片
(1) 训练
我们从迭代数据集开始。
在每次迭代期间,我们将图像传递给编码器,以获得近似后验 q(z|x) 的一组均值和对数方差参数(log-variance parameters)。
然后,我们应用 重参数化技巧 从 q(z|x) 中采样。
最后,我们将重新参数化的样本传递给解码器,以获取生成分布 p(x∣z) 的 logit。
注意:由于我们使用的是由 keras 加载的数据集,其中训练集中有 6 万个数据点,测试集中有 1 万个数据点,因此我们在测试集上的最终 ELBO 略高于对 Larochelle 版 MNIST 使用动态二值化的文献中的报告结果。这里有个 关于 logits 的 解释。
(2) 生成图片
进行训练后,可以生成一些图片了。
我们首先从单位高斯先验分布 p(z) 中采样一组潜在向量。
随后生成器将潜在样本 z 转换为观测值的 logit,得到分布 p(x∣z)。
这里我们画出伯努利分布的概率。
epochs = 100# set the dimensionality of the latent space to a plane for visualization laterlatent_dim = 2num_examples_to_generate = 16# keeping the random vector constant for generation (prediction) so# it will be easier to see the improvement.random_vector_for_generation = tf.random.normal(shape=[num_examples_to_generate, latent_dim])model = CVAE(latent_dim)def generate_and_save_images(model, epoch, test_sample):logvar = model.encode(test_sample)z = model.reparameterize(mean, logvar)predictions = model.sample(z)fig = plt.figure(figsize=(4, 4))for i in range(predictions.shape[0]):4, i + 1):, :, 0], cmap='gray')plt.axis('off')# tight_layout minimizes the overlap between 2 sub-plots:04d}.png'.format(epoch))plt.show()# Pick a sample of the test set for generating output imagesassert batch_size >= num_examples_to_generatefor test_batch in test_dataset.take(1):test_sample = test_batch[0:num_examples_to_generate, :, :, :]0, test_sample)for epoch in range(1, epochs + 1):start_time = time.time()for train_x in train_dataset:train_x, optimizer)end_time = time.time()loss = tf.keras.metrics.Mean()for test_x in test_dataset:test_x))elbo = -loss.result()=False): {}, Test set ELBO: {}, time elapse for current epoch: {}'elbo, end_time - start_time))epoch, test_sample)
一百次循环后,生成的图片如下:

图9 生成图像
同时可以生化 gif 图片来方便查看生成过程。
anim_file = 'cvae.gif'with imageio.get_writer(anim_file, mode='I') as writer:filenames = glob.glob('image*.png')filenames = sorted(filenames)for filename in filenames:image = imageio.imread(filename)writer.append_data(image)image = imageio.imread(filename)writer.append_data(image)
展示 gif 图片
import tensorflow_docs.vis.embed as embedembed.embed_file(anim_file)

图10 展示 gif 图片
6. 生成过渡图像
 图11 生成图像
图11 生成图像
参考文献
[1] Kingma D P, Welling M. Auto-Encoding Variational Bayes[J]. stat, 2014, 1050: 10.
[2] DOERSCH C. Tutorial on Variational Autoencoders[J]. stat, 2016, 1050: 13.
[3] Blei, David M., “Variational Inference.” Lecture from Princeton,
https://www.cs.princeton.edu/courses/archive/fall11/cos597C/lectures/variational-inference-i.pdf.
✄------------------------------------------------
双一流大学研究生团队创建,一个专注于目标检测与深度学习的组织,希望可以将分享变成一种习惯。
整理不易,点赞三连!
