从零实现深度学习框架(十五)动手实现Softmax回归

引言
本着“凡我不能创造的,我就不能理解”的思想,本系列文章会基于纯Python以及NumPy从零创建自己的深度学习框架,该框架类似PyTorch能实现自动求导。
要深入理解深度学习,从零开始创建的经验非常重要,从自己可以理解的角度出发,尽量不适用外部完备的框架前提下,实现我们想要的模型。本系列文章的宗旨就是通过这样的过程,让大家切实掌握深度学习底层实现,而不是仅做一个调包侠。
上篇文章对Softmax逻辑回归进行了简单的介绍,本文我们就来从零实现Softmax逻辑回归。
实现Softmax函数
首先我们实现Softmax回归的灵魂:
def softmax(x, axis=-1):
y = x.exp()
return y / y.sum(axis=axis, keepdims=True)
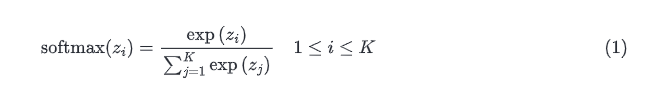
实现交叉熵损失函数

def cross_entropy(input: Tensor, target: Tensor, reduction: str = "mean") -> Tensor:
N = len(target)
p = softmax(input)
errors = - target * p.log()
# errors = - p[np.arange(N), target.data].log()
if reduction == "mean":
loss = errors.sum() / N
elif reduction == "sum":
loss = errors.sum()
else:
loss = errors
return loss
这里调用刚才实现的softmax函数把输入input转换成概率,所以这里的输入实际上是logits,即未经过Softmax的值。
然后我们基于此实现损失类:
class CrossEntropyLoss(_Loss):
def __init__(self, reduction: str = "mean") -> None:
super().__init__(reduction)
def forward(self, input: Tensor, target: Tensor) -> Tensor:
return F.cross_entropy(input, target, self.reduction)
实现Softmax回归
class SoftmaxRegression(Module):
def __init__(self, input_dim, output_dim):
self.linear = Linear(input_dim, output_dim)
def forward(self, x: Tensor) -> Tensor:
# 只要输出logits即可
return self.linear(x)
这里只需要计算出的结果即可。
使用Softmax回归分类鸢尾花
我们加载sklearn中的iris数据集。

鸢尾花如上所示,有4个特征:
Sepal.Length(花萼长度)
Sepal.Width(花萼宽度)
Petal.Length(花瓣长度)
Petal.Width(花瓣宽度)
有三个类别:Iris Setosa(山鸢尾)、Iris Versicolour(杂色鸢尾),以及Iris Virginica(维吉尼亚鸢尾)。
为了可视化的方便,我们先只考虑两个特征,可视化结果如下:
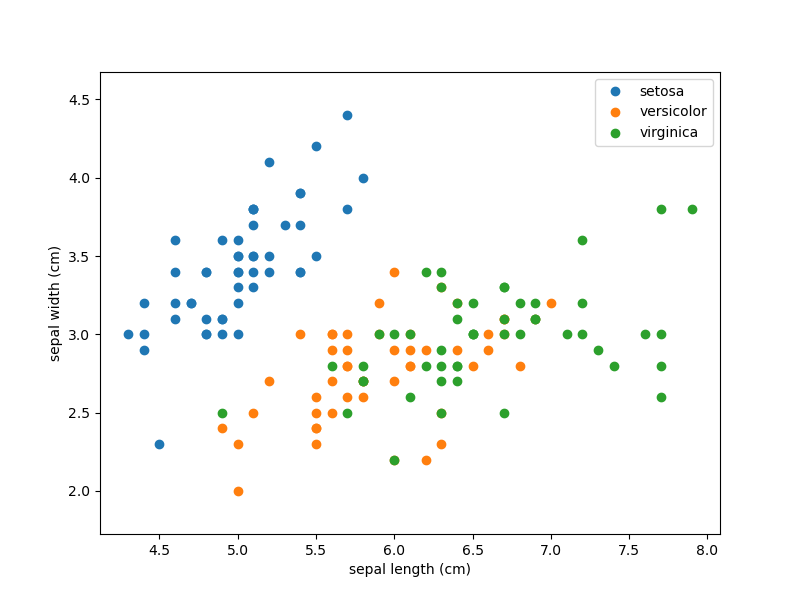
从上图可以看到,只考虑前两个特征的情况下,橙色店和绿色点看起来不太好分,这暂且不管,我们先写代码,硬Train一发。

def generate_dataset(draw_picture=False):
iris = datasets.load_iris()
X = iris['data'][:, :2] # 我们只需要前两个特征
y = iris['target']
names = iris['target_names'] # 类名
feature_names = iris['feature_names'] # 特征名
if draw_picture:
x_min, x_max = X[:, 0].min() - 0.5, X[:, 0].max() + 0.5
y_min, y_max = X[:, 1].min() - 0.5, X[:, 1].max() + 0.5
plt.figure(2, figsize=(8, 6))
plt.clf()
for target, target_name in enumerate(names):
X_plot = X[y == target]
plt.plot(X_plot[:, 0], X_plot[:, 1],
linestyle='none',
marker='o',
label=target_name)
plt.xlabel(feature_names[0])
plt.ylabel(feature_names[1])
plt.xlim(x_min, x_max)
plt.ylim(y_min, y_max)
plt.axis('equal')
plt.legend()
fig = plt.gcf()
fig.savefig('iris.png', dpi=100)
y = np.eye(3)[y]
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.2, random_state=2)
return Tensor(X_train), Tensor(X_test), Tensor(y_train), Tensor(y_test)
if __name__ == '__main__':
X_train, X_test, y_train, y_test = generate_dataset(True)
epochs = 2000
model = SoftmaxRegression(2, 3) # 2个特征 3个输出
optimizer = SGD(model.parameters(), lr=1e-1)
loss = CrossEntropyLoss()
losses = []
for epoch in range(int(epochs)):
outputs = model(X_train)
l = loss(outputs, y_train)
optimizer.zero_grad()
l.backward()
optimizer.step()
if (epoch + 1) % 20 == 0:
losses.append(l.item())
print(f"Train - Loss: {l.item()}")
# 在测试集上测试
outputs = model(X_test)
correct = np.sum(outputs.numpy().argmax(-1) == y_test.numpy().argmax(-1))
accuracy = 100 * correct / len(y_test)
print(f"Test Accuracy:{accuracy}")
为了验证泛化能力,我们这里还区分了训练集和测试集。
Train - Loss: 0.9068448543548584
Train - Loss: 0.8322725296020508
Train - Loss: 0.7793639302253723
Train - Loss: 0.740231454372406
...
Train - Loss: 0.4532046616077423
Train - Loss: 0.45260095596313477
Train - Loss: 0.45200586318969727
Train - Loss: 0.45141926407814026
Train - Loss: 0.45084092020988464
Train - Loss: 0.4502706527709961
Train - Loss: 0.44970834255218506
Train - Loss: 0.4491537809371948
Train - Loss: 0.44860681891441345
Test Accuracy:76.66666666666667
如果我们考虑所有的特征准确率会不会很一点?
我们只要修改两行代码:
def generate_dataset(draw_picture=False):
iris = datasets.load_iris()
X = iris['data'] # 修改这里
# 修改模型的参数
model = SoftmaxRegression(4, 3) # 4个特征 3个输出
再次训练查看结果:
Train - Loss: 0.7530185580253601
Train - Loss: 0.6372731328010559
Train - Loss: 0.5648812055587769
Train - Loss: 0.5048649907112122
Train - Loss: 0.44937923550605774
Train - Loss: 0.3961796164512634
Train - Loss: 0.3457953631877899
Train - Loss: 0.3021572232246399
Train - Loss: 0.27336016297340393
...
Train - Loss: 0.09917300194501877
Train - Loss: 0.09881455451250076
Train - Loss: 0.09846225380897522
Train - Loss: 0.0981159582734108
Train - Loss: 0.09777550399303436
Test Accuracy:100.0

啥也不说了。
完整代码
完整代码笔者上传到了程序员最大交友网站上去了,地址: [👉 https://github.com/nlp-greyfoss/metagrad]
总结
本文我们实现了能支持多个类别的多元逻辑回归,并且看到了在模型中充分利用已有的特征是有多重要。
最后一句:BUG,走你!


Markdown笔记神器Typora配置Gitee图床
不会真有人觉得聊天机器人难吧(一)
Spring Cloud学习笔记(一)
没有人比我更懂Spring Boot(一)
入门人工智能必备的线性代数基础
1.看到这里了就点个在看支持下吧,你的在看是我创作的动力。
2.关注公众号,每天为您分享原创或精选文章!
3.特殊阶段,带好口罩,做好个人防护。
