带容量约束的弧路径问题(CARP)简介

P1

问题背景

路径问题的研究可以分为两个方向：以点为服务对象的车辆路径问题（VRP）和以弧为服务对象的弧路径问题（ARP）。不同于前者，ARP的基本特征是车队从一个仓库出发，对所有需要服务的边进行作业，而不是在顶点进行服务。弧路径问题大致可以分为三类：中国邮路问题、乡村邮路问题和带容量约束的弧路径问题。

自1981年Golden和Wong提出带容量约束的弧路径问题（Capacitated Arc Routing Problem，简称CARP）后，CARP便普遍应用在日常生活中，特别是市政服务方面，如道路洒水车路径规划、垃圾回收车路径规划、道路除冰车路径规划、校车接送路径问题等等。

P2

问题和模型

给定一个无向图G=(V,E)，CARP有如下一些基本的定义：

虽然Golden等(1981)首次定义了CARP的数学模型，但由于模型的变量和约束会随着规模呈现指数增长，不利于求解，所以下面介绍Belenguer提出的two-index的模型定义(见参考文献[9])。首先对其他符号说明如下：

决策变量：

建立如下整数规划(IP)模型：

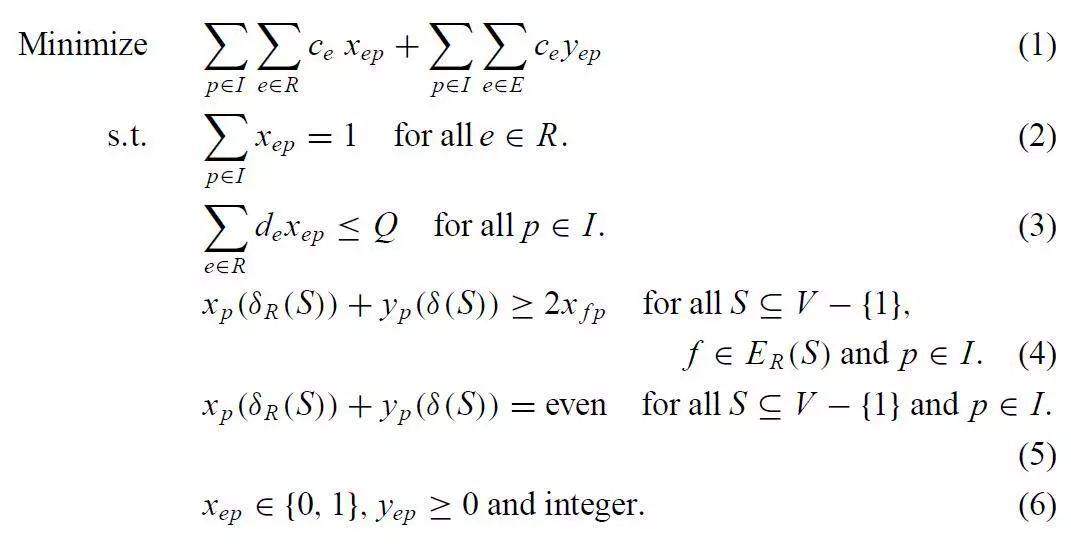
• 目标函数(1)表示最小化总行驶成本；

• 约束(2)表示所有需求边都得被服务，且每条需求边只能被一辆车服务；

• 约束(3)限制车辆不得超载；

• 约束(4)称为连接约束(connectivity constraints)，如果车p服务需求边e，那么连接这条边的路径一定连接着仓库；

• 约束(5)称为奇偶约束(parity constraint)，表示每辆车p对应的路径都是一个偶图；

• 约束(6)为决策变量的取值约束。

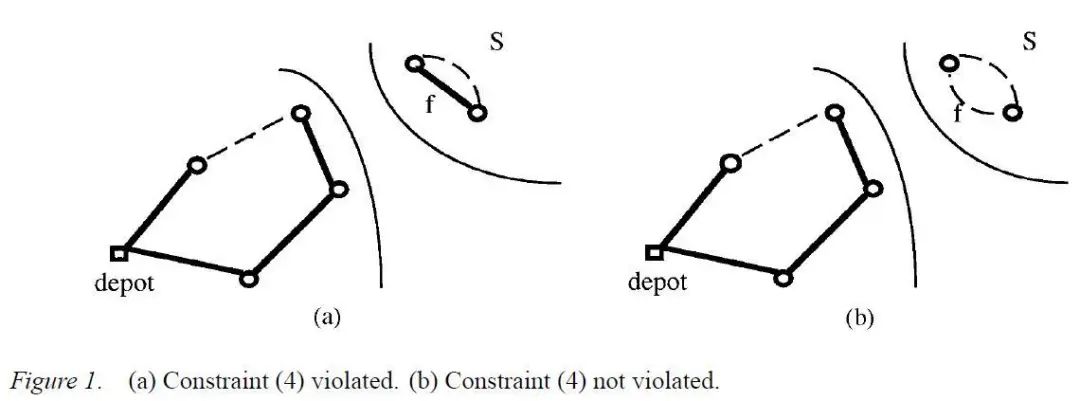
上图对约束(4)进行简单的举例描述。

图中实线表示路径服务的边，虚线表示路径空载经过的边。

对于给定的集合S和需求边f，容易看出左图违反了约束(4)，因为不等式的左边等于0，右边等于2，而右图不违反约束(4)。

P3

关于CARP的相关变式

类似于VRP大家庭里各种各样的问题，因为CARP应用的广泛性，所以学者在该问题的基础上，联系实际添加其他约束。经典的相关变式问题有：

• 混合CARP

上面提到的CARP定义在无向图G上，而现实的路径往往存在单行道和可双向行驶的道路，这时图上的需求边便包括了有向边和无向边，所以称为混合CARP

• 周期性CARP

该问题将某一段时间区域根据不同的服务需求进行分层，对各个层次确定特定的服务任务，隔几天服务一次，主要适用于需求不规律的事件，如城市电路检查等不需每天进行服务

• 带时间窗CARP

该问题是指对于某些路径只能在规定的某个时间段进行服务，如道路除冰任务一般规定在早上完成，或者问题中对个别重要路径限制了比较短的服务时间窗

• 带补给点CARP

该问题是指车辆在道路进行服务过程中，中途的顶点可以对服务车进行原料补充。如道路洒水车作业时，水箱的补给由道路的消防栓提供，而不用回到仓库

P4

求解算法介绍

对于CARP及其变式问题的求解方法有很多，有些算法可以得出确定的值，而有些算法只是对解的逼近，但具有更强的适应性。下面以CARP问题为例，从精确算法和元启发式算法的角度分别介绍一些代表性方法。

▽

4.1  精确算法

精确算法可以大致分为三类：

I.  Cutting plane algorithm

基于上述的原模型CARP，定义变量z_e表示每条属于边集E的边e被deadhead的次数，从而生成一些有效不等式，在规模不大的实例中可以快速得到一个不错的下界，见Belenguer and Benavent (2003)。 

II.  Branch-Cut

将原模型CARP转化成等价的CVRP，并使用分支切平面算法解决，见 Baldacci and Maniezzo (2006)。

III.  Branch-Price-Cut

将原模型CARP转化为set partition模型，但这样将会生成许多变量（路径），所以利用列生成处理，然后在松弛模型通过添加割平面使模型更紧，见Pecin and Uchoa(2019)。

▽

4.2  元启发式算法

进入21世纪后，更多的启发式算法文献偏向于元启发式算法的设计，最流行的是邻域搜索算法，相关文献包括：

• Hertz等(2000)提出了禁忌搜索算法

• Polacek等(2008)利用变邻域搜索算法进行求解

另一类解决CARP的热门元启发式算法是基于种群的算法，相关文献包括：

• Santos等(2010)基于元启发式设计了蚁群算法，对初始种群生成、决策准则和局部搜索算子进行了改进

• Chen等(2016b) 基于模因搜索框架(memetic search framework)设计了混合元启发算法，在局部搜索过程中，将随机化禁忌阈值法(randomized tabu thresholding procedure)和不可行下降法(infeasible descent procedure)结合加以改进。

以上选取的是求解CARP比较高引的文章，有很强的参考意义，感兴趣的同志可以下载一读，下载链接请移步留言区。

其中，参考文献[8]是一本详细介绍ARP前世今生的书籍《Arc Routing: Problems, Methods, and Applications》。

P5

参考文献

[1] José M. Belenguer, Benavent E (2003) A cutting plane algorithm for the capacitated arc routing problem. Computers & Operations Research 30(5):705-728.

[2] Baldacci R , Maniezzo V (2006) Exact methods based on node-routing formulations for undirected arc-routing problems. Networks 47(1):52-60.

[3] Diego Pecin, Eduardo Uchoa (2019) Comparative Analysis of Capacitated Arc Routing Formulations for Designing a New Branch-Cut-and-Price Algorithm. Transportation Science 53(6):1673-1694.

[4] Hertz, A., Laporte, G., and Mittaz, M. (2000). A tabu search heuristic for the capacitated arc routing problem. Operations research, 48(1):129–135.

[5] Polacek, M., Doerner, K. F., Hartl, R. F., and Maniezzo, V. (2008). A variable neighborhood search for the capacitated arc routing problem with intermediate facilities. Journal of Heuristics, 14(5):405–423.

[6] Santos, L., Coutinho-Rodrigues, J., and Current, J. R. (2010). An improved ant colony optimization based algorithm for the capacitated arc routing problem. Transportation Research Part B: Methodological, 44(2):246–266.

[7] Chen, L., Gendreau, M., H`a, M. H., and Langevin, A. (2016a). A robust optimization approach for the road network daily maintenance routing problem with uncertain service time. Transportation research part E: logistics and transportation review, 85:40–51.

[8] Laporte G . Arc Routing: Problems, Methods, and Applications[M]. Society for Industrial and Applied Mathematics, 2015.

[9] Belenguer J M , Benavent E . The Capacitated Arc Routing Problem: Valid Inequalities and Facets[J]. Computational Optimization and Applications, 1998, 10(2):165-187.

 赞 赏 

---The End---