如何爬升用于机器学习的测试集-技术圈

爬坡测试集是一种在不影响训练集甚至开发预测模型的情况下，在机器学习竞赛中实现良好或完美预测的方法。作为机器学习竞赛的一种方法，这是理所当然的，大多数竞赛平台都对其施加了限制，以防止出现这种情况，这一点很重要。但是，爬坡测试集是机器学习从业人员在参加比赛时不小心做的事情。通过开发一个明确的实现来爬升测试集，它有助于更好地了解通过过度使用测试数据集来评估建模管道而过度拟合测试数据集的难易程度。

在本教程中，您将发现如何爬升用于机器学习的测试集。完成本教程后，您将知道：

无需查看训练数据集，就可以通过爬上测试集来做出完美的预测。
如何为分类和回归任务爬坡测试集。
当我们过度使用测试集来评估建模管道时，我们暗中爬升了测试集。

教程概述

本教程分为五个部分。他们是：

爬坡测试仪
爬山算法
如何进行爬山
爬坡糖尿病分类数据集
爬坡房屋回归数据集

爬坡测试仪

像Kaggle上的机器学习比赛一样，机器学习比赛提供了完整的训练数据集以及测试集的输入。给定比赛的目的是预测目标值，例如测试集的标签或数值。针对隐藏的测试设置目标值评估解决方案，并进行适当评分。与测试集得分最高的参赛作品赢得了比赛。机器学习竞赛的挑战可以被定义为一个优化问题。传统上，竞赛参与者充当优化算法，探索导致不同组预测的不同建模管道，对预测进行评分，然后对管道进行更改以期望获得更高的分数。此过程也可以直接用优化算法建模，无需查看训练集就可以生成和评估候选预测。通常，这称为爬山测试集，作为解决此问题的最简单的优化算法之一就是爬山算法。尽管在实际的机器学习竞赛中应该正确地爬升测试集，但是实施该方法以了解该方法的局限性和过度安装测试集的危险可能是一个有趣的练习。此外，无需接触训练数据集就可以完美预测测试集的事实常常使很多初学者机器学习从业人员感到震惊。最重要的是，当我们反复评估不同的建模管道时，我们暗中爬升了测试集。风险是测试集的分数得到了提高，但代价是泛化误差增加，即在更广泛的问题上表现较差。进行机器学习竞赛的人们都非常清楚这个问题，并且对预测评估施加了限制以应对该问题，例如将评估限制为每天一次或几次，并在测试集的隐藏子集而不是整个测试集上报告分数。。有关更多信息，请参阅进一步阅读部分中列出的论文。接下来，让我们看看如何实施爬坡算法来优化测试集的预测。

爬山算法

爬山算法是一种非常简单的优化算法。它涉及生成候选解决方案并进行评估。然后是逐步改进的起点，直到无法实现进一步的改进，或者我们用光了时间，资源或兴趣。从现有候选解决方案中生成新的候选解决方案。通常，这涉及对候选解决方案进行单个更改，对其进行评估，并且如果候选解决方案与先前的当前解决方案一样好或更好，则将该候选解决方案接受为新的“当前”解决方案。否则，将其丢弃。我们可能会认为只接受分数更高的候选人是一个好主意。对于许多简单问题，这是一种合理的方法，尽管在更复杂的问题上，希望接受具有相同分数的不同候选者，以帮助搜索过程缩放要素空间中的平坦区域（高原）。当爬上测试集时，候选解决方案是预测列表。对于二进制分类任务，这是两个类的0和1值的列表。对于回归任务，这是目标变量范围内的数字列表。对候选分类解决方案的修改将是选择一个预测并将其从0翻转为1或从1翻转为0。对回归进行候选解决方案的修改将是将高斯噪声添加到列表中的一个值或替换一个值在列表中使用新值。解决方案的评分涉及计算评分指标，例如分类任务的分类准确性或回归任务的平均绝对误差。现在我们已经熟悉了算法，现在就来实现它。

如何进行爬山

我们将在综合分类任务上开发爬坡算法。首先，我们创建一个包含许多输入变量和5,000行示例的二进制分类任务。然后，我们可以将数据集分为训练集和测试集。下面列出了完整的示例。

# example of a synthetic dataset.
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
# define dataset
X, y = make_classification(n_samples=5000, n_features=20, n_informative=15, n_redundant=5, random_state=1)
print(X.shape, y.shape)
# split dataset
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.33, random_state=1)
print(X_train.shape, X_test.shape, y_train.shape, y_test.shape)

运行示例首先报告创建的数据集的形状，显示5,000行和20个输入变量。然后将数据集分为训练集和测试集，其中约3,300个用于训练，约1,600个用于测试。

(5000, 20) (5000,)
(3350, 20) (1650, 20) (3350,) (1650,)

现在我们可以开发一个登山者。首先，我们可以创建一个将加载的函数，或者在这种情况下，定义数据集。当我们要更改数据集时，可以稍后更新此功能。

# load or prepare the classification dataset
def load_dataset():
 return make_classification(n_samples=5000, n_features=20, n_informative=15, n_redundant=5, random_state=1)

接下来，我们需要一个函数来评估候选解决方案，即预测列表。我们将使用分类精度，其中分数范围在0（最坏的解决方案）到1（完美的预测集）之间。

# evaluate a set of predictions
def evaluate_predictions(y_test, yhat):
 return accuracy_score(y_test, yhat)

接下来，我们需要一个函数来创建初始候选解决方案。这是0和1类标签的预测列表，长度足以匹配测试集中的示例数，在这种情况下为1650。我们可以使用randint（）函数生成0和1的随机值。

# create a random set of predictions
def random_predictions(n_examples):
 return [randint(0, 1) for _ in range(n_examples)]

接下来，我们需要一个函数来创建候选解决方案的修改版本。在这种情况下，这涉及在解决方案中选择一个值并将其从0翻转为1或从1翻转为0。通常，我们会在爬坡期间对每个新的候选解决方案进行一次更改，但是我已经对该函数进行了参数化，因此您可以根据需要探索多个更改。

# modify the current set of predictions
def modify_predictions(current, n_changes=1):
 # copy current solution
 updated = current.copy()
 for i in range(n_changes):
  # select a point to change
  ix = randint(0, len(updated)-1)
  # flip the class label
  updated[ix] = 1 - updated[ix]
 return updated

到现在为止还挺好。接下来，我们可以开发执行搜索的功能。首先，通过调用random_predictions（）函数和随后的validate_predictions（）函数来创建和评估初始解决方案。然后，我们循环进行固定次数的迭代，并通过调用Modify_predictions（）生成一个新的候选值，对其进行求值，如果分数与当前解决方案相同或更好，则将其替换。当我们完成预设的迭代次数（任意选择）或达到理想分数时，该循环结束，在这种情况下，我们知道其精度为1.0（100％）。下面的函数hill_climb_testset（）实现了此功能，将测试集作为输入并返回在爬坡过程中发现的最佳预测集。

# run a hill climb for a set of predictions
def hill_climb_testset(X_test, y_test, max_iterations):
 scores = list()
 # generate the initial solution
 solution = random_predictions(X_test.shape[0])
 # evaluate the initial solution
 score = evaluate_predictions(y_test, solution)
 scores.append(score)
 # hill climb to a solution
 for i in range(max_iterations):
  # record scores
  scores.append(score)
  # stop once we achieve the best score
  if score == 1.0:
   break
  # generate new candidate
  candidate = modify_predictions(solution)
  # evaluate candidate
  value = evaluate_predictions(y_test, candidate)
  # check if it is as good or better
  if value >= score:
   solution, score = candidate, value
   print('>%d, score=%.3f' % (i, score))
 return solution, scores

这里的所有都是它的。下面列出了爬坡测试装置的完整示例。

# example of hill climbing the test set for a classification task
from random import randint
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
from matplotlib import pyplot
 
# load or prepare the classification dataset
def load_dataset():
 return make_classification(n_samples=5000, n_features=20, n_informative=15, n_redundant=5, random_state=1)
 
# evaluate a set of predictions
def evaluate_predictions(y_test, yhat):
 return accuracy_score(y_test, yhat)
 
# create a random set of predictions
def random_predictions(n_examples):
 return [randint(0, 1) for _ in range(n_examples)]
 
# modify the current set of predictions
def modify_predictions(current, n_changes=1):
 # copy current solution
 updated = current.copy()
 for i in range(n_changes):
  # select a point to change
  ix = randint(0, len(updated)-1)
  # flip the class label
  updated[ix] = 1 - updated[ix]
 return updated
 
# run a hill climb for a set of predictions
def hill_climb_testset(X_test, y_test, max_iterations):
 scores = list()
 # generate the initial solution
 solution = random_predictions(X_test.shape[0])
 # evaluate the initial solution
 score = evaluate_predictions(y_test, solution)
 scores.append(score)
 # hill climb to a solution
 for i in range(max_iterations):
  # record scores
  scores.append(score)
  # stop once we achieve the best score
  if score == 1.0:
   break
  # generate new candidate
  candidate = modify_predictions(solution)
  # evaluate candidate
  value = evaluate_predictions(y_test, candidate)
  # check if it is as good or better
  if value >= score:
   solution, score = candidate, value
   print('>%d, score=%.3f' % (i, score))
 return solution, scores
 
# load the dataset
X, y = load_dataset()
print(X.shape, y.shape)
# split dataset into train and test sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.33, random_state=1)
print(X_train.shape, X_test.shape, y_train.shape, y_test.shape)
# run hill climb
yhat, scores = hill_climb_testset(X_test, y_test, 20000)
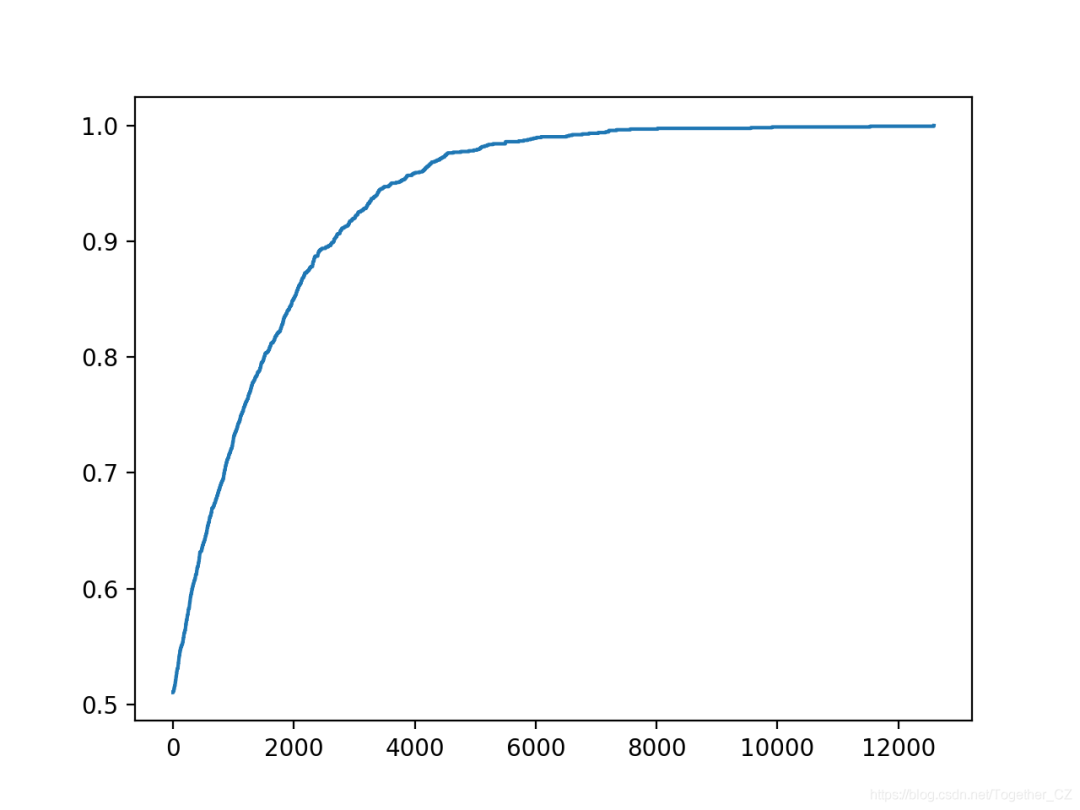
# plot the scores vs iterations
pyplot.plot(scores)
pyplot.show()

运行示例将使搜索进行20,000次迭代，或者如果达到理想的准确性，则停止搜索。注意：由于算法或评估程序的随机性，或者数值精度的差异，您的结果可能会有所不同。考虑运行该示例几次并比较平均结果。在这种情况下，我们在约12,900次迭代中找到了一组理想的测试集预测。回想一下，这是在不接触训练数据集且不通过查看测试集目标值进行欺骗的情况下实现的。相反，我们只是简单地优化了一组数字。这里的教训是，将测试管道用作爬山优化算法，对测试集重复建模管道的评估会做同样的事情。解决方案将过度适合测试集。

...
>8092, score=0.996
>8886, score=0.997
>9202, score=0.998
>9322, score=0.998
>9521, score=0.999
>11046, score=0.999
>12932, score=1.000

还创建了优化进度图。这有助于了解优化算法的更改（例如，在坡道上更改内容的选择以及更改方式）如何影响搜索的收敛性。

爬坡糖尿病分类数据集

我们将使用糖尿病数据集作为探索爬坡测试集以解决分类问题的基础。每条记录都描述了女性的医疗细节，并且预测是未来五年内糖尿病的发作。

数据集详细信息：pima-indians-diabetes.names数据集：pima-indians-diabetes.csv

数据集有八个输入变量和768行数据；输入变量均为数字，目标具有两个类别标签，例如这是一个二进制分类任务。下面提供了数据集前五行的示例。

6,148,72,35,0,33.6,0.627,50,1
1,85,66,29,0,26.6,0.351,31,0
8,183,64,0,0,23.3,0.672,32,1
1,89,66,23,94,28.1,0.167,21,0
0,137,40,35,168,43.1,2.288,33,1
...

我们可以使用Pandas直接加载数据集，如下所示。

# load or prepare the classification dataset
def load_dataset():
 url = 'https://raw.githubusercontent.com/jbrownlee/Datasets/master/pima-indians-diabetes.csv'
 df = read_csv(url, header=None)
 data = df.values
 return data[:, :-1], data[:, -1]

其余代码保持不变。创建该文件是为了使您可以放入自己的二进制分类任务并进行尝试。下面列出了完整的示例。

# example of hill climbing the test set for the diabetes dataset
from random import randint
from pandas import read_csv
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
from matplotlib import pyplot
 
# load or prepare the classification dataset
def load_dataset():
 url = 'https://raw.githubusercontent.com/jbrownlee/Datasets/master/pima-indians-diabetes.csv'
 df = read_csv(url, header=None)
 data = df.values
 return data[:, :-1], data[:, -1]
 
# evaluate a set of predictions
def evaluate_predictions(y_test, yhat):
 return accuracy_score(y_test, yhat)
 
# create a random set of predictions
def random_predictions(n_examples):
 return [randint(0, 1) for _ in range(n_examples)]
 
# modify the current set of predictions
def modify_predictions(current, n_changes=1):
 # copy current solution
 updated = current.copy()
 for i in range(n_changes):
  # select a point to change
  ix = randint(0, len(updated)-1)
  # flip the class label
  updated[ix] = 1 - updated[ix]
 return updated
 
# run a hill climb for a set of predictions
def hill_climb_testset(X_test, y_test, max_iterations):
 scores = list()
 # generate the initial solution
 solution = random_predictions(X_test.shape[0])
 # evaluate the initial solution
 score = evaluate_predictions(y_test, solution)
 scores.append(score)
 # hill climb to a solution
 for i in range(max_iterations):
  # record scores
  scores.append(score)
  # stop once we achieve the best score
  if score == 1.0:
   break
  # generate new candidate
  candidate = modify_predictions(solution)
  # evaluate candidate
  value = evaluate_predictions(y_test, candidate)
  # check if it is as good or better
  if value >= score:
   solution, score = candidate, value
   print('>%d, score=%.3f' % (i, score))
 return solution, scores
 
# load the dataset
X, y = load_dataset()
print(X.shape, y.shape)
# split dataset into train and test sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.33, random_state=1)
print(X_train.shape, X_test.shape, y_train.shape, y_test.shape)
# run hill climb
yhat, scores = hill_climb_testset(X_test, y_test, 5000)
# plot the scores vs iterations
pyplot.plot(scores)
pyplot.show()

运行示例将报告每次搜索过程中看到改进时的迭代次数和准确性。

在这种情况下，我们使用的迭代次数较少，因为要进行的预测较少，因此优化起来比较简单。

注意：由于算法或评估程序的随机性，或者数值精度的差异，您的结果可能会有所不同。考虑运行该示例几次并比较平均结果。

在这种情况下，我们可以看到在大约1,500次迭代中达到了完美的精度。

...
>617, score=0.961
>627, score=0.965
>650, score=0.969
>683, score=0.972
>743, score=0.976
>803, score=0.980
>817, score=0.984
>945, score=0.988
>1350, score=0.992
>1387, score=0.996
>1565, score=1.000

还创建了搜索进度的折线图，表明收敛迅速。

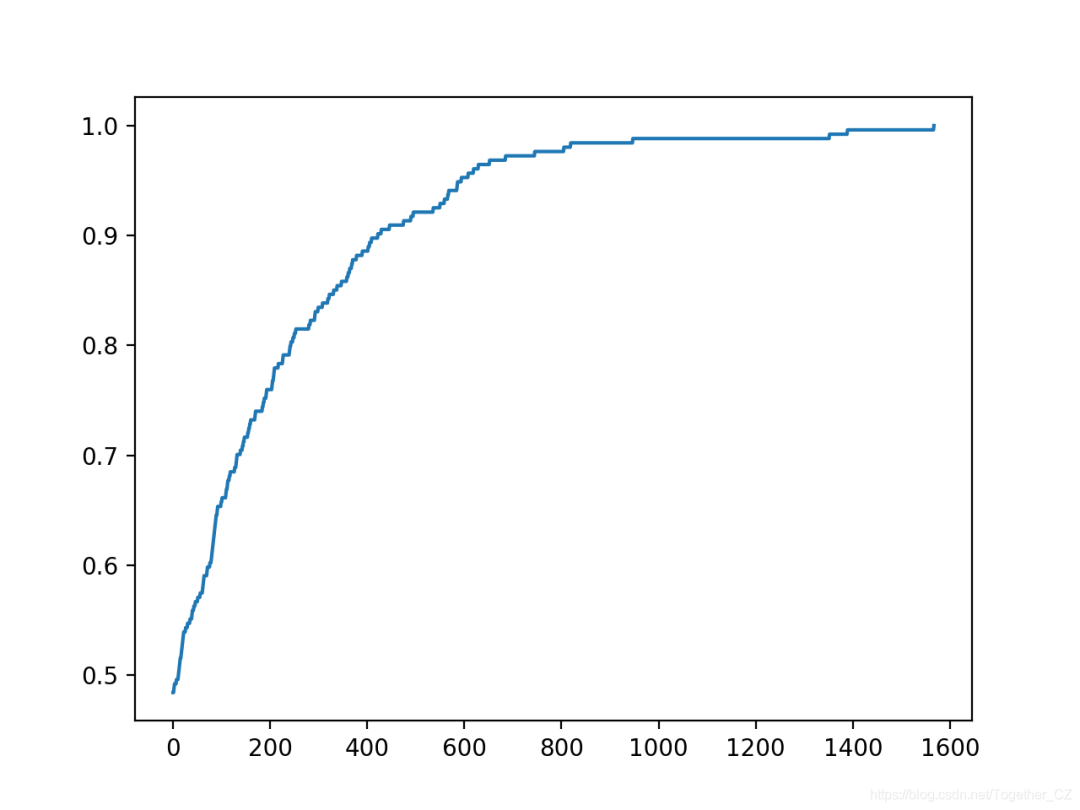
爬坡房屋回归数据集

我们将使用住房数据集作为探索爬坡测试集回归问题的基础。住房数据集包含给定房屋及其附近地区详细信息的数千美元房屋价格预测。

数据集详细信息：housing.names数据集：housing.csv

这是一个回归问题，这意味着我们正在预测一个数值。共有506个观测值，其中包含13个输入变量和一个输出变量。下面列出了前五行的示例。

0.00632,18.00,2.310,0,0.5380,6.5750,65.20,4.0900,1,296.0,15.30,396.90,4.98,24.00
0.02731,0.00,7.070,0,0.4690,6.4210,78.90,4.9671,2,242.0,17.80,396.90,9.14,21.60
0.02729,0.00,7.070,0,0.4690,7.1850,61.10,4.9671,2,242.0,17.80,392.83,4.03,34.70
0.03237,0.00,2.180,0,0.4580,6.9980,45.80,6.0622,3,222.0,18.70,394.63,2.94,33.40
0.06905,0.00,2.180,0,0.4580,7.1470,54.20,6.0622,3,222.0,18.70,396.90,5.33,36.20
...

首先，我们可以更新load_dataset（）函数以加载住房数据集。作为加载数据集的一部分，我们将标准化目标值。由于我们可以将浮点值限制在0到1的范围内，这将使爬坡的预测更加简单。通常不需要这样做，只是此处采用的简化搜索算法的方法。

# load or prepare the classification dataset
def load_dataset():
 url = 'https://raw.githubusercontent.com/jbrownlee/Datasets/master/housing.csv'
 df = read_csv(url, header=None)
 data = df.values
 X, y = data[:, :-1], data[:, -1]
 # normalize the target
 scaler = MinMaxScaler()
 y = y.reshape((len(y), 1))
 y = scaler.fit_transform(y)
 return X, y

接下来，我们可以更新评分函数，以使用预期值和预测值之间的平均绝对误差。

# evaluate a set of predictions
def evaluate_predictions(y_test, yhat):
 return mean_absolute_error(y_test, yhat)

我们还必须将解决方案的表示形式从0和1标签更新为介于0和1之间的浮点值。必须更改初始候选解的生成以创建随机浮点列表。

# create a random set of predictions
def random_predictions(n_examples):
 return [random() for _ in range(n_examples)]

在这种情况下，对解决方案所做的单个更改以创建新的候选解决方案，包括简单地用新的随机浮点数替换列表中的随机选择的预测。我选择它是因为它很简单。

# modify the current set of predictions
def modify_predictions(current, n_changes=1):
 # copy current solution
 updated = current.copy()
 for i in range(n_changes):
  # select a point to change
  ix = randint(0, len(updated)-1)
  # flip the class label
  updated[ix] = random()
 return updated

更好的方法是将高斯噪声添加到现有值，我将其作为扩展留给您。如果您尝试过，请在下面的评论中告诉我。例如：

# add gaussian noise
updated[ix] += gauss(0, 0.1)

最后，必须更新搜索。最佳值现在是错误0.0，如果发现错误，该错误将用于停止搜索。

# stop once we achieve the best score
if score == 0.0:
 break

我们还需要将搜索从最大分数更改为现在最小分数。

# check if it is as good or better
if value <= score:
 solution, score = candidate, value
 print('>%d, score=%.3f' % (i, score))

下面列出了具有这两个更改的更新的搜索功能。

# run a hill climb for a set of predictions
def hill_climb_testset(X_test, y_test, max_iterations):
 scores = list()
 # generate the initial solution
 solution = random_predictions(X_test.shape[0])
 # evaluate the initial solution
 score = evaluate_predictions(y_test, solution)
 print('>%.3f' % score)
 # hill climb to a solution
 for i in range(max_iterations):
  # record scores
  scores.append(score)
  # stop once we achieve the best score
  if score == 0.0:
   break
  # generate new candidate
  candidate = modify_predictions(solution)
  # evaluate candidate
  value = evaluate_predictions(y_test, candidate)
  # check if it is as good or better
  if value <= score:
   solution, score = candidate, value
   print('>%d, score=%.3f' % (i, score))
 return solution, scores

结合在一起，下面列出了用于回归任务的测试集爬坡的完整示例。

# example of hill climbing the test set for the housing dataset
from random import random
from random import randint
from pandas import read_csv
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_absolute_error
from sklearn.preprocessing import MinMaxScaler
from matplotlib import pyplot
 
# load or prepare the classification dataset
def load_dataset():
 url = 'https://raw.githubusercontent.com/jbrownlee/Datasets/master/housing.csv'
 df = read_csv(url, header=None)
 data = df.values
 X, y = data[:, :-1], data[:, -1]
 # normalize the target
 scaler = MinMaxScaler()
 y = y.reshape((len(y), 1))
 y = scaler.fit_transform(y)
 return X, y
 
# evaluate a set of predictions
def evaluate_predictions(y_test, yhat):
 return mean_absolute_error(y_test, yhat)
 
# create a random set of predictions
def random_predictions(n_examples):
 return [random() for _ in range(n_examples)]
 
# modify the current set of predictions
def modify_predictions(current, n_changes=1):
 # copy current solution
 updated = current.copy()
 for i in range(n_changes):
  # select a point to change
  ix = randint(0, len(updated)-1)
  # flip the class label
  updated[ix] = random()
 return updated
 
# run a hill climb for a set of predictions
def hill_climb_testset(X_test, y_test, max_iterations):
 scores = list()
 # generate the initial solution
 solution = random_predictions(X_test.shape[0])
 # evaluate the initial solution
 score = evaluate_predictions(y_test, solution)
 print('>%.3f' % score)
 # hill climb to a solution
 for i in range(max_iterations):
  # record scores
  scores.append(score)
  # stop once we achieve the best score
  if score == 0.0:
   break
  # generate new candidate
  candidate = modify_predictions(solution)
  # evaluate candidate
  value = evaluate_predictions(y_test, candidate)
  # check if it is as good or better
  if value <= score:
   solution, score = candidate, value
   print('>%d, score=%.3f' % (i, score))
 return solution, scores
 
# load the dataset
X, y = load_dataset()
print(X.shape, y.shape)
# split dataset into train and test sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.33, random_state=1)
print(X_train.shape, X_test.shape, y_train.shape, y_test.shape)
# run hill climb
yhat, scores = hill_climb_testset(X_test, y_test, 100000)
# plot the scores vs iterations
pyplot.plot(scores)
pyplot.show()

运行示例将在搜索过程中每次看到改进时报告迭代次数和MAE。

在这种情况下，我们将使用更多的迭代，因为要优化它是一个更复杂的问题。选择的用于创建候选解决方案的方法也使它变慢了，也不太可能实现完美的误差。实际上，我们不会实现完美的错误；相反，如果错误达到的值低于最小值（例如1e-7）或对目标域有意义的值，则最好停止操作。这也留给读者作为练习。例如：

# stop once we achieve a good enough
if score <= 1e-7:
 break

注意：由于算法或评估程序的随机性，或者数值精度的差异，您的结果可能会有所不同。考虑运行该示例几次并比较平均结果。

在这种情况下，我们可以看到在运行结束时实现了良好的错误。

>95991, score=0.001
>96011, score=0.001
>96295, score=0.001
>96366, score=0.001
>96585, score=0.001
>97575, score=0.001
>98828, score=0.001
>98947, score=0.001
>99712, score=0.001
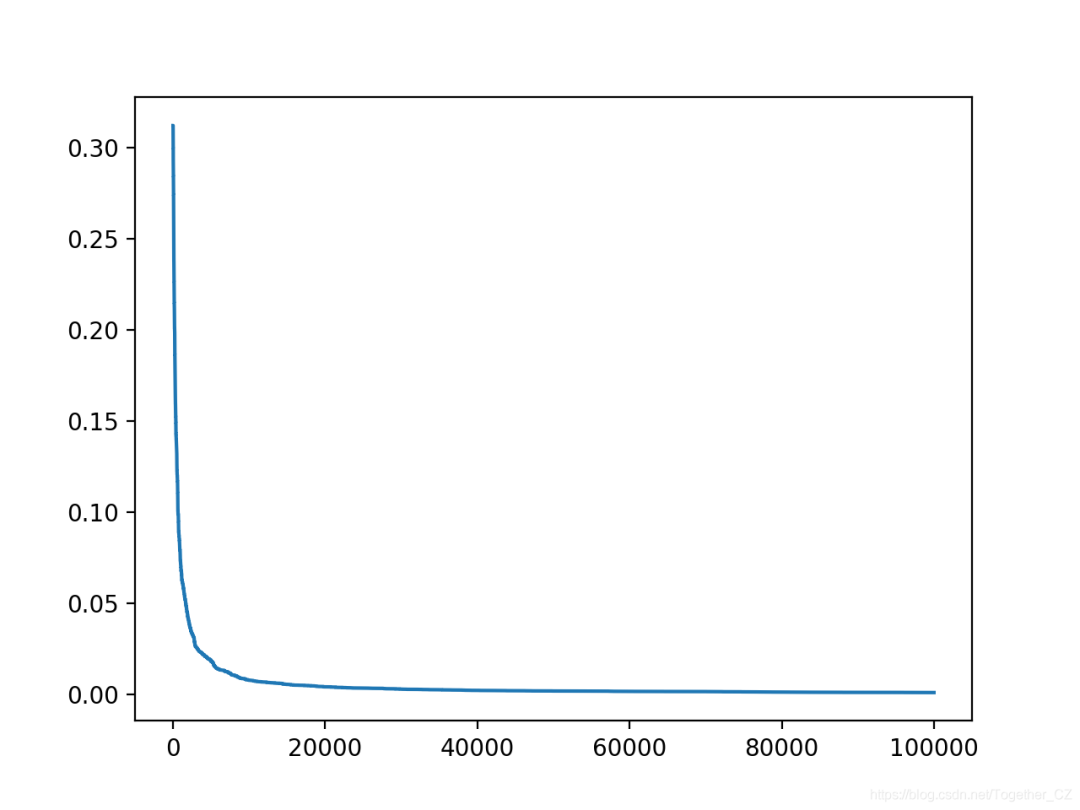
>99913, score=0.001

还创建了搜索进度的折线图，显示收敛速度很快，并且在大多数迭代中保持不变。

作者：沂水寒城，CSDN博客专家，个人研究方向：机器学习、深度学习、NLP、CV

Blog: http://yishuihancheng.blog.csdn.net

赞赏作者

更多阅读

2020 年最佳流行 Python 库 Top 10

2020 Python中文社区热门文章 Top 10

5分钟快速掌握 Python 定时任务框架

特别推荐

点击下方阅读原文加入社区会员