用Python解决挖黄金矿问题


问题描述
有 5 座金矿,每座金矿黄金储量不同,需要参与挖掘的工人数目也不同。假定有 10 个工人,每座金矿要么全挖,要么不挖,不可以拆分,请问要想得到最多的黄金,应该选择挖取哪几座金矿?金矿的信息如表 1 所示。
表 1 金矿信息
| 金 矿 编 号 |
所需工人数量 |
黄金存储量 |
| 1 |
5人 |
400kg |
| 2 |
5人 |
500kg |
| 3 |
3人 |
200kg |
| 4 |
4人 |
300kg |
| 5 |
3人 |
350kg |
解析问题
拿到这样一个题目,你会想到用什么算法解决呢?仔细阅读一下,有没有和背包问题很像呢?背包问题用的是动态规划算法,那么,这个问题我们试着用动态规划算法。首先我们将挖矿问题创建一个网格,如图 9 所示。
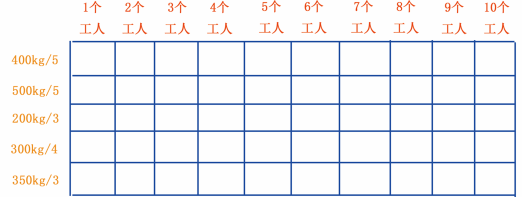
图 9 挖矿网格
从图 9 可以看出,网格的各行代表挖矿的价值以及需要的人数,各列是工人数(工人拆分成 1~10 人),网格最初是空的,等我们填满网格,就能找到答案了。
400kg/5 行
我们先来看 400kg/5 这行,忽略下面的 500kg/5 、 200kg/3 、 300kg/4 、 350kg/3 行,如图 10 所示。
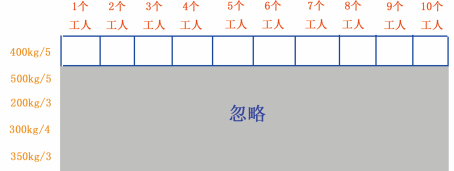
图 10 400kg/5 行
先来看第 1 个单元格, 1 个工人不能挖 400kg 的金矿,因此第一个单元格的存储量是 0kg ,如图 11 所示。
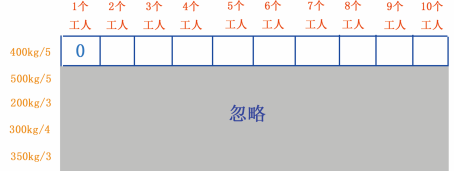
图 11 填第 1 个单元格
根据问题的要求,需要 5 个工人才能挖 400kg 的金矿,因此单元格 2~4 都不能挖 400kg 的金矿, 2~4 的单元格的存储量都是 0kg ,如图 12 所示。
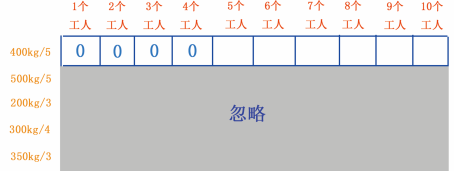
图 12 填第 2~4 个单元格
到第 5 个单元格,有足够的工人可以挖 400kg 的金矿了,因此第 5 个单元格的存储量是 400kg ,如图 13 所示。
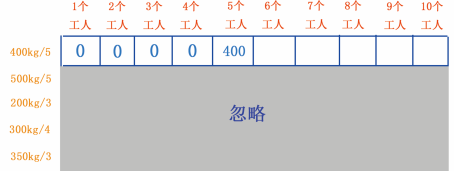
图 13 填第 5 个单元格
只要超过 5 人,都能挖 400kg 的金矿,只不过剩余的工人就可以休息了。因此第 6~10 单元格的存储量也是 400kg ,如图 14 所示。
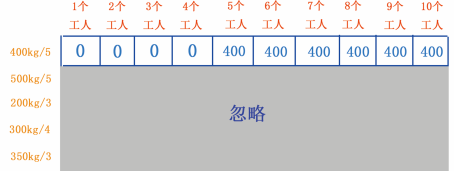
图 14 填第 6~10 个单元格
图 14 已经将 400kg/5 行网格填满,这行表示的最大值是 400 ,也就是说如果有 10 个工人,可挖金矿最大的黄金存储量是 400kg 。显然这不是最优解,接下来接着讲解。
500kg/5 行
我们再来看 500kg/5 这行,忽略下面的 200kg/3 、 300kg/4 、 350kg/3 行,如图 15 所示。
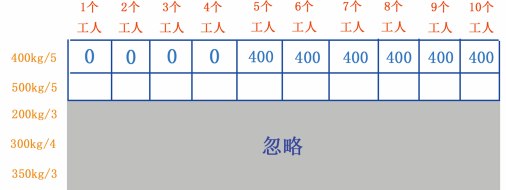
图 15 500kg/5 行
先来看第 1~4 个单元格, 1~4 个工人都不能挖 500kg 的金矿,因此 500kg/5 行第 1~4 个单元格为 0kg ,如图 16 所示。
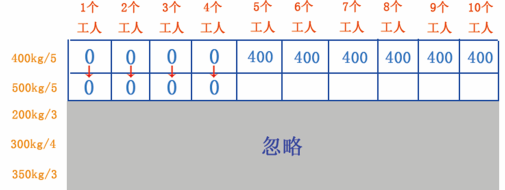
图 16 填第 1~4 个单元格
再来填第 5~9 个单元格,有 5 个工人就能挖 500kg 的金矿,从 400kg/5 行可知, 5~9 个工人的可挖存储量是 400kg ,而 500 大于 400 ,因此,数据进行更新, 5~9 个工人可挖存储量是 500kg ,如 图 17 所示。
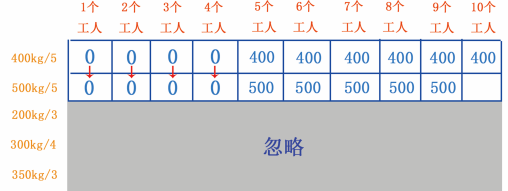
图 17 填第 5~9 个单元格
再来看一下第 10 个单元格, 5 个工人可以挖 400kg 的金矿, 5 个工人可以挖 500kg 的金矿,那么 10 个工人就可以分工同时挖 400kg 和 500kg 的金矿,因此当有 10 个工人时,可挖 400+500=900kg 的黄金存储量,如图 18 所示。
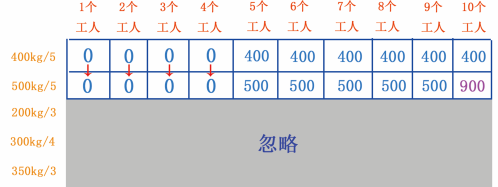
图 18 第 10 个单元格
从图 18 可以看出,已经将 500kg/5 行填满,此时最大的可挖黄金存储量更新了,变成了 900 。我们再接着看下一行网格的情况。
200kg/3 行
我们再来看 200kg/3 这行,忽略下面的 300kg/4 、 350kg/3 行,如图 19 所示。
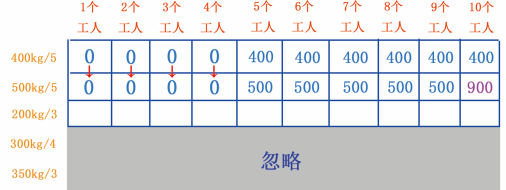
图 19 200kg/3 行
根据问题含义,可知 200kg 的金矿需要 3 个工人,因此第 1 , 2 个单元格的可挖黄金存储量依然是 0kg ,如图 20 所示。
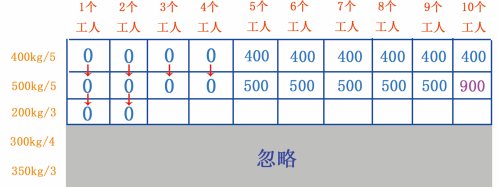
图 20 填第 1 , 2 个单元格
当有 3 个工人时,就可以挖 200kg 的金矿了,之前 500kg/5 行所求 3 个工人可挖黄金 0kg , 200 比 0 大,因此第 3 个单元格存储量更新了,如图 21 所示。
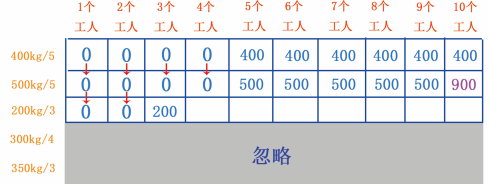
图 21 填第 3 个单元格
当有 4 个工人时,也只能挖 200kg 的金矿,因此第 4 个单元格的最大黄金存储量是 200kg ,如图 22 所示。
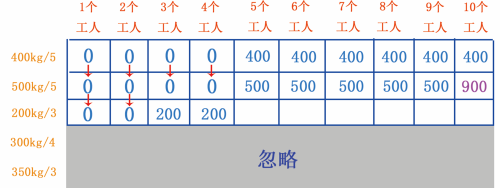
图 22 填第 4 个单元格
当有 5~7 个工人时,能挖 200kg 的金矿,但是在 500kg/5 行的 5~7 个工人可挖的最大黄金存储量是 500kg , 500 大于 200 ,因此第 5~7 个单元格的黄金存储量依然是 500kg ,如图 23 所示。
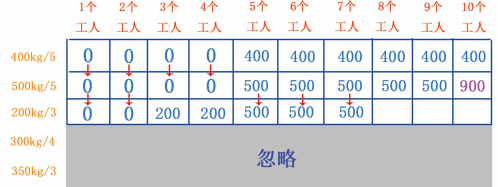
图 23 填第 5~7 个单元格
再来看当有 8~9 个工人时的情况,可以分 3 人挖 200kg 的金矿,剩下的人可以挖 500kg 的金矿,这样算来,可以挖 200+500=700kg 的金矿, 500kg/5 行的 8~9 单元格是 500 ,很明显, 700 大于 500 ,因此数据进行更新,如图 24 所示。
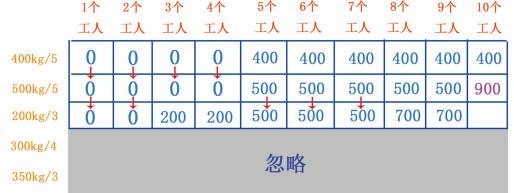
图 24 填第 8~9 个单元格
再来看 , 当有 10 个工人时,从 500kg/5 行求得的最大可挖存储量是 900kg ,如果分 3 人挖 200kg 的金矿,剩余 7 人只能挖最大存储量是 500 的金矿,相加之后是 700 , 700 小于 900 ,因此第 10 个单元格依然是 500kg/5 行求得的 900 ,如图 25 所示。
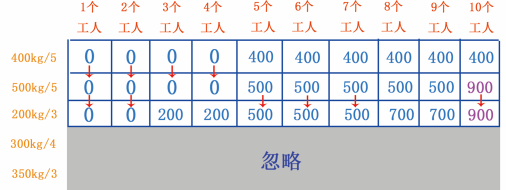
图 25 填第 10 个单元格
从图 25 可以看出,最大可挖黄金存储量是 900kg ,接着寻找 300kg/4 行。
300kg/4 行
我们再来看 300kg/4 这行,忽略下面的 350kg/3 行,如图 26 所示。
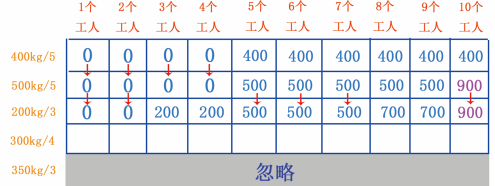
图 26 350kg/3 行
当有 1~2 个工人时,不能挖 300kg 的金矿,因此第 1 , 2 个单元格的值 0 ,当有 3 个工人时,也不能挖 300kg 的金矿,因此第 3 个单元格的最大可挖存储量是 200kg/3 行的值 200 ,如 图 27 所示。
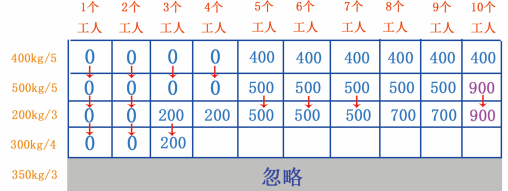
图 27 填第 1~3 个单元格
从 200kg/3 行可以看出当前第 4 个单元格的最大值是 200 ,可是当有 4 个工人时,就可以挖 300kg 的金矿了, 300 比 200 大,因此更新第 4 个单元格的值,如图 28 所示。
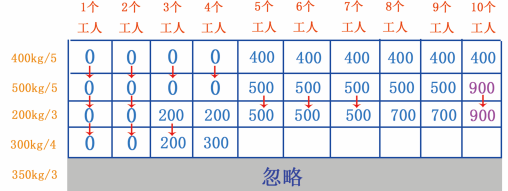
图 28 更新第 4 个单元格
当有 5~7 个工人时,可以挖 300kg 的金矿,但是很明显, 300 小于 500 ,因此第 5~7 个单元格依然是 500 ;当有 8 个工人时,能分 4 人挖 300kg 的金矿,剩余的 4 人只能挖 200kg 的金矿, 300+200=500 ,而从 200kg/3 行可知当前最大值是 700 ,很明显 700 大于 500 ,因此第 8 个单元格依然是 700 ,如图 29 所示。
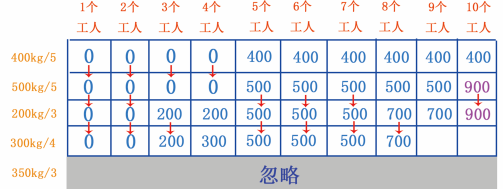
图 29 填第 5~8 个单元格
当有 9 个工人时,可以分 4 人挖 300kg 的金矿,分 5 人挖 500kg 的金矿,此时总共可以挖 300+500=800kg 的金矿, 800 比 700 大,因此更新数据,如图 30 所示。
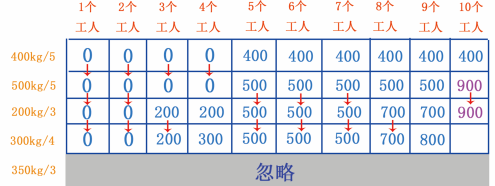
图 30 填第 9 个单元格
当有 10 个工人时,之前计算的最大值是 900 , 10 个工人可以分 4 个工人挖 300kg ,剩下的 6 人最多可挖 500kg 的金矿,加起来是 800kg , 800 小于 900 ,因此第 10 个单元格依然是 900 ,如图 31 所示。
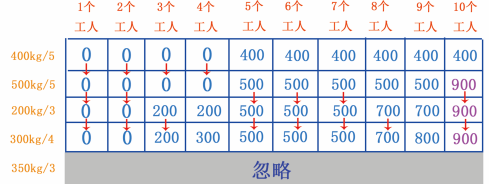
图 31 填第 10 个单元格
从图 31 可以看出,此时的最大可挖黄金存储量是依然是 900kg ,接下来看 350kg/3 行。有没有可能更新最大值。
350kg/3 行
我们再来看 350kg/3 行,如图 32 所示。
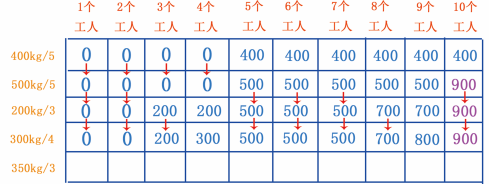
图 32 350kg/3 行
当有 1~2 个工人时,不能挖 350kg 的金矿,因此最大可挖黄金存储量依然是 0kg ,而当有 3 个工人时,可以挖 350kg 的金矿, 350 大于 200 ,更新数据;当有 4 个工人时,也可以挖 350kg 金矿, 350 大于 300 ,更新数据,如图 33 所示。
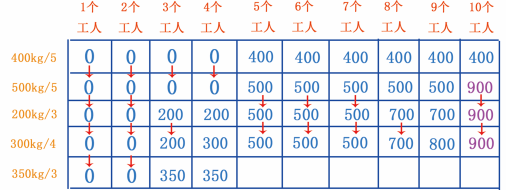
图 33 填第 1~4 个单元格
当有 5 个工人时,可以挖 350kg 的金矿,但是 500 比 350 大,因此第 5 个单元格依然是 500 。而当有 6 个工人时,可以分 3 个人挖 350kg 的金矿,剩余 3 个人挖 200kg 的金矿,因此是 350+200=550kg 的金矿, 550 比 500 大,因此更新数据,如图 34 所示。
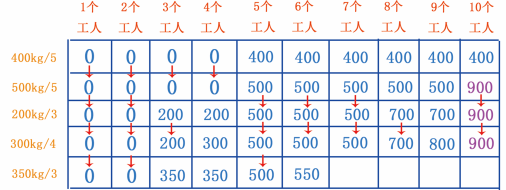
图 34 填第 5 、 6 个单元格
当有 7 个工人时,可以分 3 人挖 350kg 的金矿,分 4 人挖 300kg 的金矿,一共可以挖 350+300=650kg 的金矿, 650 大于 500 ,更新数据;当有 8 个工人时,可以分 3 个工人挖 350kg 的金矿,分 5 个工人挖 500kg 的金矿,一共可以挖 350+500=850kg , 850 大于 700 ,更新数据,如图 35 所示。
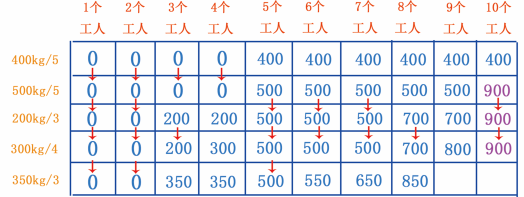
图 35 填第 7 、 8 个单元格
当有 9 个工人时,可以分 3 个工人挖 350kg 的金矿,剩余人挖 500kg 的金矿,一共可以挖 350+500=850kg 的金矿, 850 大于 800 ,更新数据;当有 10 个工人时,拆分工人挖矿之后的最大值是 850 , 850 小于 900 ,因此第 10 个单元格依然是 900 ,如图 36 所示。
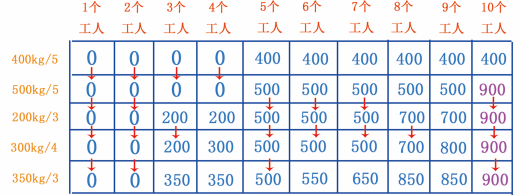
图 36 填第 9 、 10 个单元格
从图 36 可以看出,此时已经填满了挖矿网格,也发现 10 个工人最大可挖黄金存储量是 900kg ,挖的金矿是 400kg/5 和 500kg/5 这两座金矿。
3 代码实现
从第 14.6.2 节中的分析来看,可以用动态规划算法来实现挖黄金矿问题,从图 14.10~ 图 14.36 可知,我们每填一个单元格,使用的公式都是相同的,公式如图 37 所示。

图 37 公式
我们可以利用图 37 所示的公式来填写每个单元格,最终的单元格和图 36 一致。
实例 8 挖黄金矿问题
具体代码如下:
"""
功能:自定义挖黄金矿函数,实现动态规划算法
参数说明: count :表示矿的数量
TotalWorkers: 表示总的工人数
workers :表示每个矿需要的工人数
gold :表示每个金矿黄金储量
"""
def mine (count, TotalWorkers, workers, gold):
# 置零,表示初始状态
reserves = [[0 for j in range (TotalWorkers + 1)] for i in range (count +1)]
for i in range (1, count+1): # 遍历物每座矿,从第 1 座矿计算
for j in range (1, TotalWorkers + 1): # 遍历工人数
reserves[i][j] = reserves[i - 1][j] # 定义 reserves 数组存储黄金的最大储存量
# 有足够工人挖矿,遍历前一个状态考虑是否置换
if j >= workers[i - 1] and reserves[i][j] < reserves[i - 1][j - workers[i - 1]] + gold[i - 1]:
# 最大存储量就是:当前存储量 + 剩余工人可挖存储量
reserves[i][j] = reserves[i - 1][j - workers[i - 1]] +gold[i - 1]
for x in reserves: # 遍历输出挖矿网格
print (x)
return reserves # 返回最大黄金的储存量
"""
功能:自定义显示输出结果函数
参数说明: count :表示矿的数量
TotalWorkers: 表示总的工人数
workers :表示每个矿需要的工人数
reserves :表示最大价值,即所求的结果
"""
def show (count, TotalWorkers, workers, reserves):
x = [ False for i in range (count)] # 初始化 x ,使得 x 为假
j = TotalWorkers # 工人总人数赋给变量 j
for i in range (count, 0, -1): # 遍历每座矿
# 如果 reserves[i][j] 单元格大于上一行同列的单元格的值,进行更新
if reserves[i][j] > reserves[i - 1][j]:
x[i - 1] = True
j -= workers[i - 1] # 工人数减去上一行同列的单元格使用的工人数
print ( ' 可挖最大存储量为 :' , reserves[count][TotalWorkers]) # 输出最大存储量的值
print ( ' 要挖的金矿为 :' )
for i in range (count):
if x[i]:
print ( ' 第 ' , i + 1, ' 个矿 ' , end = '' )
count = 5 # 一共有 5 座矿
TotalWorkers = 10 # 一共有 10 个工人
workers = [5,5,3,4,3] # 每个矿需要的工人数
gold = [400,500,200,300,350] # 每个矿的存储黄金量
reserves = mine(count, TotalWorkers, workers, gold) # 调用 mine() 函数动态规划算法函数
show(count, TotalWorkers, workers, reserves) # 调用 show() 函数输出结果
程序运行结果如图 38 所示。
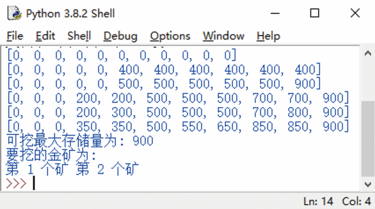
图 38 挖黄金矿问题
从图 38 的结果来看,和图 36 分析的结果一致。最后输出的所挖的金矿是第 1 个和第 2 个,即 400kg/5 和 500kg/5 。

