每日一道 LeetCode (42):旋转数组

❝每天 3 分钟,走上算法的逆袭之路。
❞
前文合集
代码仓库
GitHub:https://github.com/meteor1993/LeetCode
Gitee:https://gitee.com/inwsy/LeetCode
题目:旋转数组
题目来源:https://leetcode-cn.com/problems/rotate-array/
给定一个数组,将数组中的元素向右移动 k 个位置,其中 k 是非负数。
示例 1:
输入: [1,2,3,4,5,6,7] 和 k = 3
输出: [5,6,7,1,2,3,4]
解释:
向右旋转 1 步: [7,1,2,3,4,5,6]
向右旋转 2 步: [6,7,1,2,3,4,5]
向右旋转 3 步: [5,6,7,1,2,3,4]
示例 2:
输入: [-1,-100,3,99] 和 k = 2
输出: [3,99,-1,-100]
解释:
向右旋转 1 步: [99,-1,-100,3]
向右旋转 2 步: [3,99,-1,-100]
说明:
- 尽可能想出更多的解决方案,至少有三种不同的方法可以解决这个问题。
- 要求使用空间复杂度为 O(1) 的 原地 算法。
解题方案一:暴力法
暴力解题大家应该都想得到,就是用两个循环套起来,然后加一个中间变量来逐位替换位置。
public void rotate(int[] nums, int k) {
int temp, previous;
for (int i = 0; i < k; i++) {
previous = nums[nums.length - 1];
for (int j = 0; j < nums.length; j++) {
temp = nums[j];
nums[j] = previous;
previous = temp;
}
}
}
运行时长又超过 3 位数了,智商不行的人可能就单纯的比较适合看答案。
解题方案二:使用额外的数组
这竟然都算一个解题方案,题目上不是说要求使用空间复杂度为 O(1) 的 原地 算法么?
还带这么玩的啊!
好吧好吧,你是答案,你说了算,你说啥都对。
能用额外数组这个题就很简单了,直接新建一个数组,然后把每个元素直接放在正确的位置上,最后放完以后再用这个数组对原数组挨个赋值。
public void rotate_1(int[] nums, int k) {
int[] a = new int[nums.length];
for (int i = 0; i < nums.length; i++) {
a[(i + k) % nums.length] = nums[i];
}
for (int i = 0; i < nums.length; i++) {
nums[i] = a[i];
}
}
时间下降到 1ms ,有这么立竿见影的么,不过只超过了 57.17% 的人,说明还有更快的方案,接着往下看答案。
解题方案三:使用环状替换
这个方案有点意思,确实很难想,我就借用下官方的图做下解释:
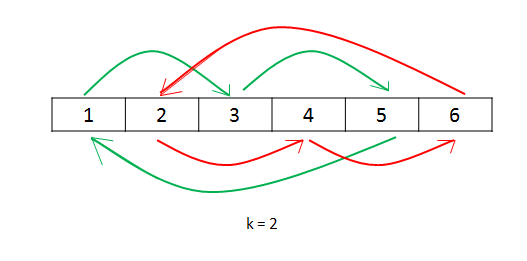
这个图是是画了一个数组的移动过程:
nums: [1, 2, 3, 4, 5, 6]
k: 2
- 第一次移动,从第一个 1 开始, 1 向后移动两位,到了 3 现在的位置,这时我们需要将 1 放到位置 3 上。
- 第二次移动,因为 3 没有了位置,我们接着计算 3 要移动的位置,发现 3 要移动到位置 5 上,那么我们把 3 移动过去。
- 第三次移动,现在是 5 没有了位置,计算 5 需要的位置,在位置 1 上,而位置 1 现在正好空着,我们把 5 放进去。
- 第四次移动,开始画红线的部分,现在我们该移动位置 2 上的数字 2 了, 2 需要移动到位置 4 上,我们把 2 移动过去。
- ......
剩下的两次移动我就不写了,和绿线部分是一致的。
当整体移动完成后,整个数组我们实际上只循环了一次,就完成了所有的移动,这个时间复杂度是 O(n) 。
下面的代码上注释我已经都写好了,就不再解释了:
public void rotate_2(int[] nums, int k) {
// 先计算 k ,这个 k 为当前需要移动的位置,防止 k 超出数组长度
k = k % nums.length;
// 初始化移动的次数
int count = 0;
for (int start = 0; count < nums.length; start++) {
// 初始化当前位置
int current = start;
// 初始化要移动的数
int prev = nums[start];
do {
// 计算目标要移动的位置
int next = (current + k) % nums.length;
// 定义中间变量
int tmp = nums[next];
// 将要移动的数字进行赋值
nums[next] = prev;
// 这时,接着移动刚才被挤掉位置的数
prev = tmp;
// 变化当前的位置为刚才移动的位置
current = next;
// 将操作次数 +1
count++;
} while (start != current);
}
}
果然只遍历一次耗时足够低,不过时间复杂度为 O(n) 的还有下面的另一种思路。
解题方案四:使用反转
这个操作也是相当的骚,我是真的服。
答案上是这么解释这个方案的:
这个方法基于这个事实:当我们旋转数组 k 次, k % n 个尾部元素会被移动到头部,剩下的元素会被向后移动。
这句话看完我一脸懵,这是说了个啥?然后接着往下看。
在这个方法中,我们首先将所有元素反转。然后反转前 k 个元素,再反转后面 n - k 个元素,就能得到想要的结果。
这句话是看懂了,但是没明白意思,直到看到了题目上举的例子才看懂:
假设 n=7 且 k=3 。
原始数组 : 1 2 3 4 5 6 7
反转所有数字后 : 7 6 5 4 3 2 1
反转前 k 个数字后 : 5 6 7 4 3 2 1
反转后 n-k 个数字后 : 5 6 7 1 2 3 4 --> 结果
妈耶,这还是人能想出来的方案么?这题套路这么深还能算是一道简单题么?
方案有了实际上代码就很简单了:
public void rotate_3(int[] nums, int k) {
k = k % nums.length;
reverse(nums, 0, nums.length - 1);
reverse(nums, 0, k - 1);
reverse(nums, k, nums.length - 1);
}
private void reverse(int[] nums, int start, int end) {
while (start < end) {
int temp = nums[start];
nums[start] = nums[end];
nums[end] = temp;
start++;
end--;
}
}
这后面的简单题是越来越难了,严重感觉自己现在智商不够用,看来是时候买点猪头肉补补了。

