【一天一道Leetcode】数组不可变

本篇推文共计2000个字,阅读时间约3分钟。
01
题目描述

题目描述:
给定一个整数数组nums,求出数组从索引i到j(i≤j)范围内元素的总和,包含i、j两点。
实现 NumArray 类:
NumArray(int[] nums) 使用数组 nums 初始化对象
int sumRange(int i,int j)
返回数组 nums 从索引i到j(i≤j)范围内元素的总和,包含i、j两点。
也就是 sum(nums[i], nums[i+1],...nums[j])
sumRange会被反复调用无数次,请设计一个时间复杂度最低的算法以降低时间消耗。
示例输入:
["NumArray","sumRange", "sumRange", "sumRange"]
[[[-2,0,3,-5,2,-1]], [0,2], [2,5],[0,5]]示例输出:
[null,1,-1,-3]示例解释:
NumArray numArray = new NumArray([-2,0,3,-5,2,-1]);
numArray.sumRange(0, 2);
return 1
#因为((-2)+0+3)=1
numArray.sumRange(2, 5);
return -1
#因为(3+(-5)+2 +(-1))=-1
numArray.sumRange(0, 5);
return -3
#因为((-2)+0+3+(-5)+2+(-1))=-302
代码分析
看到这题可能很多人会选择使用一个for循环来解决,但是请注意题目中强调的
sumRange会被反复调用无数次,请设计一个时间复杂度最低的算法降低时间消耗
如果使用for循环解决的话,每次调用sumRange时,通过循环的方法计算数组nums从下标i到下标j范围内的元素和,需要计算 j−(i-1) 个元素的和。
由于每次检索的时间和检索的下标范围有关,因此检索的时间复杂度较高,如果检索次数较多,则会超出时间限制。
同时题目中也强调sumRange会多次调用,如果仅使用for循环,每次用于检索的时间较长,多次使用后检索的总时间就会增长的很快。

因此为了降低算法的检索总时间,
我们采用前缀和presums的方法解决该题。
前缀和的概念
其实来源于sumRange(i,j)的数学形式变换
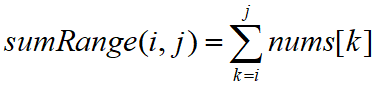
对公式进行变换可得:
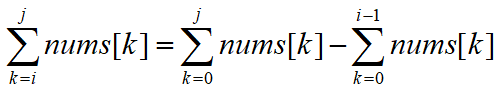
所以学好数学很重要!!!

由此可知,要计算sumRange(i,j),
则需要计算数组nums在下标j和下标i-1的前缀和,
然后再计算两个前缀和的差。
同时如果我们在函数初始化的时候
就计算出数组nums在每个下标处的前缀和,
即满足每次调用sumRange时的时间复杂度都为O(1)

既然理论知识我们懂了,那么实际用法如何呢?
假设数组nums的长度为n,创建长度为n+1的前缀和数组presums,
对于0<=i<n,
则有presums[i+1]=presums[i]+nums[i]
对于0<i<=n,
则presums[i]表示数组nums从下标0到下标i-1的前缀和我们用图片来直观的解释:
如下图所示:
设nums=[0,1,4,6,3,7],presums[0]=0
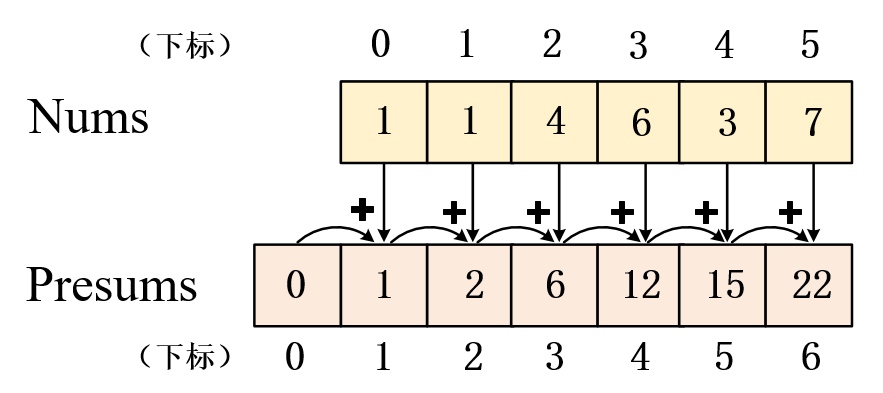
将前缀和数组presums的长度设为n+1的目的
是为了方便计算sumRange(i,j)
同时也不需要对i=0的情况特殊处理。
所以本题中:
sumRange(i,j)= presums[j+1]- presums[i]
则我们本题的实现代码如下:
class NumArray:
def __init__(self, nums: List[int]):
self.presums=[0]
_pre=self.presums
for num in nums:
_pre.append(_pre[-1]+num)
#_pre[-1]+num的含义就是上图中的+号步骤,presums中的最后一个数与当前的nums数值相加
def sumRange(self, i: int, j: int) -> int:
_pre=self.presums
return _pre[j+1] - _pre[i]
【年终总结】你好2021,再见2020。

【快速写好毕业论文】你不得不知晓的七个常用文献搜索平台

【秋招纪实录】一篇特别正经的【腾讯】求职经验分享

【一天一道Leetcode】两数之和

【一天一道Leetcode】单调数列

【秋招纪实录】一篇特别正经的【无领导小组讨论】经验分享
你与世界
只差一个
公众号

