用 Python 来实现 RSA 加解密
昨天看到一篇英文文章[1],展示了如何用 Python 来实现 RSA 算法,代码的逻辑与前文一文搞懂 RSA 算法一样,不太熟悉 RSA 的朋友可以看一下一文搞懂 RSA 算法,里面对什么是 RSA,RSA 的数学原理进行了说明,并举了一个简单的例子,可以说是全知乎最容易读懂 RSA 的文章了(这话来自读者评论),要是看不懂,你加我微信「somenzz」交流一下。
这篇英文提供的代码我运行了下,发现不能加密中文,于是就修改了下加解密的函数,让其支持中文加解密。今天的文章就分享一下如何用 Python 来实现 RSA 加解密的这一过程,帮助你建立 RSA 的直观认识,代码里的随机素数生成算法,也值得我们学习。
0、效果演示
咱们先看下效果。
原文:“有内鬼,终止交易”
密文,根本无法破解:
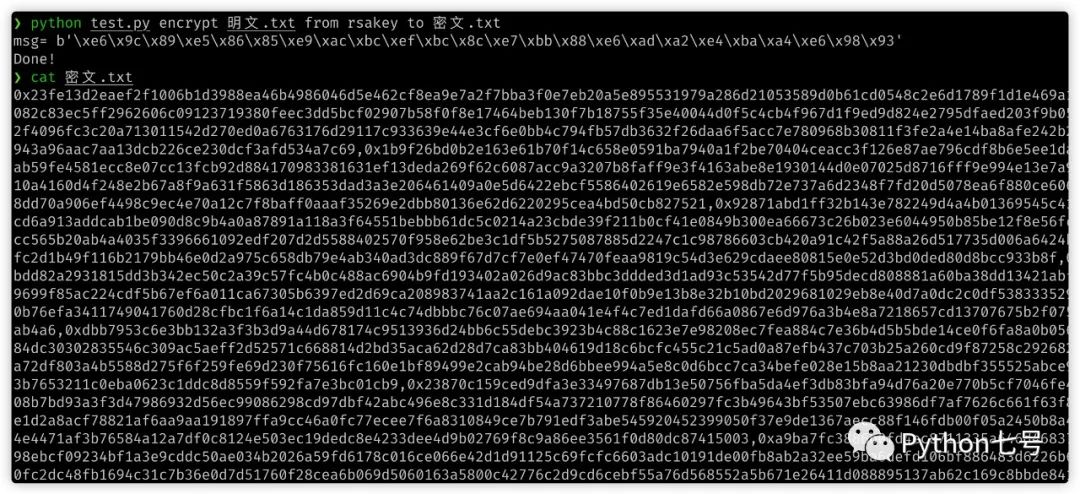
解密之后:
完整代码公众号「Python七号」回复「rsa」获取。
1、密钥对的生成
思路:
1)随机找两个质数(素数) p 和 q,p 与 q 越大,越安全,这里选择 1024 位的质数:
p = genprime(1024)
q = genprime(1024)
genprime() 函数的实现过程先不说。
2)计算他们的乘积 n = p * q 及 欧拉函数 lambda_n。
n = p * q
lambda_n = (p - 1) * (q - 1)
3)随机选择一个整数 e,条件是 1 < e < lambda_n,且 e 与 lambda_n 互质。比如选择 35537,35537 只有 16 位,必然小于 lambda_n。
e = 35537
4)找到一个整数 d,可以使得 e * d 除以 lambda_n 的余数为 1,并返回密钥对。
d = eucalg(e, lambda_n)[0]
if d < 0: d += lambda_n
return (d, n), (e, n)
eucalg 函数的实现放后面说。
至此,密钥对的生成的函数如下:
def create_keys():
p = genprime(1024)
q = genprime(1024)
n = p * q
lambda_n = (p - 1) * (q - 1)
e = 35537
d = eucalg(e, lambda_n)[0]
if d < 0: d += lambda_n
return (d, n), (e, n)
2、加解密的实现
加密和解密的过程是一样的,公钥加密,私钥解密,反过来也可以,私钥加密,公钥解密,只不过前者我们叫加密,后者我们叫签名。
具体的函数实现如下:
def encrypt_data(data,key):
e_data = []
for d in data:
e = modpow(d, key[0], key[1])
e_data.append(e)
return e_data
## 加密和解密的逻辑完全一样
decrypt_data = encrypt_data
这里面用到了 modpow 函数,它用来计算公式 b^e % n = r 的。
如果是加密过程,那么 b 是明文,(n,e)为公钥,r 为密文。 如果是解密过程,那么 b 是密文,(n,d)为私钥,r 为名文。
modpow 的定义如下:
def modpow(b, e, n):
# find length of e in bits
tst = 1
siz = 0
while e >= tst:
tst <<= 1
siz += 1
siz -= 1
# calculate the result
r = 1
for i in range(siz, -1, -1):
r = (r * r) % n
if (e >> i) & 1: r = (r * b) % n
return r
3、随机质数的生成函数
随机质数的生成函数,其中用到了矩阵乘法和斐波那契数列,可见数学对于算法的重要性。
# matrix multiplication
def sqmatrixmul(m1, m2, w, mod):
mr = [[0 for j in range(w)] for i in range(w)]
for i in range(w):
for j in range(w):
for k in range(w):
mr[i][j] = (mr[i][j] + m1[i][k] * m2[k][j]) % mod
return mr
# fibonacci calculator
def fib(x, mod):
if x < 3: return 1
x -= 2
# find length of e in bits
tst = 1
siz = 0
while x >= tst:
tst <<= 1
siz += 1
siz -= 1
# calculate the matrix
fm = [
# function matrix
[0, 1],
[1, 1]
]
rm = [
# result matrix
# (identity)
[1, 0],
[0, 1]
]
for i in range(siz, -1, -1):
rm = sqmatrixmul(rm, rm, 2, mod)
if (x >> i) & 1:
rm = sqmatrixmul(rm, fm, 2, mod)
# second row of resulting vector is result
return (rm[1][0] + rm[1][1]) % mod
def genprime(siz):
while True:
num = (1 << (siz - 1)) + secrets.randbits(siz - 1) - 10;
# num must be 3 or 7 (mod 10)
num -= num % 10
num += 3 # 3 (mod 10)
# heuristic test
if modpow(2, num - 1, num) == 1 and fib(num + 1, num) == 0:
return num
num += 5 # 7 (mod 10)
# heuristic test
if modpow(2, num - 1, num) == 1 and fib(num + 1, num) == 0:
return num
4、eucalg 函数的实现
函数的本质在于求下面二元一次方程的解:
e * x - lambda_n * y =1
具体代码:
def eucalg(a, b):
# make a the bigger one and b the lesser one
swapped = False
if a < b:
a, b = b, a
swapped = True
# ca and cb store current a and b in form of
# coefficients with initial a and b
# a' = ca[0] * a + ca[1] * b
# b' = cb[0] * a + cb[1] * b
ca = (1, 0)
cb = (0, 1)
while b != 0:
# k denotes how many times number b
# can be substracted from a
k = a // b
# swap a and b so b is always the lesser one
a, b, ca, cb = b, a-b*k, cb, (ca[0]-k*cb[0], ca[1]-k*cb[1])
if swapped:
return (ca[1], ca[0])
else:
return ca
5、测试
test.py 脚本使用方法:
1、生成密钥
python test.py make-keys rsakey
公钥保存在 rsakey.pub 中, 私钥保存在 rsakey.priv 中
2、对文件内容加密
假如有文件 明文.txt:
python test.py encrypt 明文.txt from rsakey to 密文.txt
将生成 密文.txt
3、 对文件内容解密
假如有文件 密文.txt:
python test.py decrypt 密文.txt as rsakey to 解密后.txt
将生成 解密后.txt
最后的话
本文分享了 RSA 算法的 Python 的简单实现,可以帮助理解 RSA 算法,获取完整代码关注公众号「Python七号」,回复「rsa」获取。
扫码关注
参考资料英文文章: https://coderoasis.com/implementing-rsa-in-python-from-scratch-part-2/
