3D激光雷达和相机的外部校准-技术圈

标题：Set-Membership Extrinsic Calibration of a 3D LiDAR and a Camera

作者：Raphael Voges and Bernardo Wagner

来源：IROS 2020

编译：姚瀚晨

审核：wyc

本文转载自泡泡机器人SLAM。

摘要

大家好，今天为大家带来的文章是—— 集员法对3D激光雷达和相机的外部校准（Set-Membership Extrinsic Calibration of a 3D LiDAR and a Camera）。

这篇文章与传感器的融合相关，主要介绍了3D激光雷达和相机校准时候是如何考虑不同传感器之间的误差的；
为了融合来自3D激光雷达和相机的信息，需要知道传感器坐标系之间的外部校准。

传统的外部校准方案有三个缺点：

传统的校准方法忽略了传感器误差，导致了校准失真；
传统的校准方法假设了初始平均误差为0，默认传感器每次测量接近真实值，这种假设常常失效。例如，激光雷达入射角和反射率带来的误差，可能会导致激光雷达偏移的情形；
传统的校准方法不能评估提取特征的准确性，因此不能在外部校准的时候不能通过调整特征的权重提高准确性。

本文创新点：

提出了一种基于图像的检测方法，该方法将YOLOv3架构扩展为具有3D质心损失和中级特征融合，以利用这两种方式的互补信息；
介绍基于间距的方法（interval-based approaches）来提取图像和激光点云的相应特征；
利用间距的特征设定约束满足问题（Constraint Satisfaction Problem, CSP），在仿真和实验中验证了准确性。

贡献

提出了一种基于图像的检测方法，该方法将YOLOv3架构扩展为具有3D质心损失和中级特征融合，以利用这两种方式的互补信息；
介绍基于间距的方法（interval-based approaches）来提取图像和激光点云的相应特征；
利用间距的特征设定约束满足问题（Constraint Satisfaction Problem, CSP），在仿真和实验中验证了准确性。

方法介绍

如图1所示，间隔向量（interval vectors）形成了一个框（scan box），包围了实际测量的一些点集。通过使用扫描框，可以得到平面的垂直矢量（plane normal vector）、边界线的矢量（line direction vectors）、标定棋盘的四个角上的点（corner boxes）。

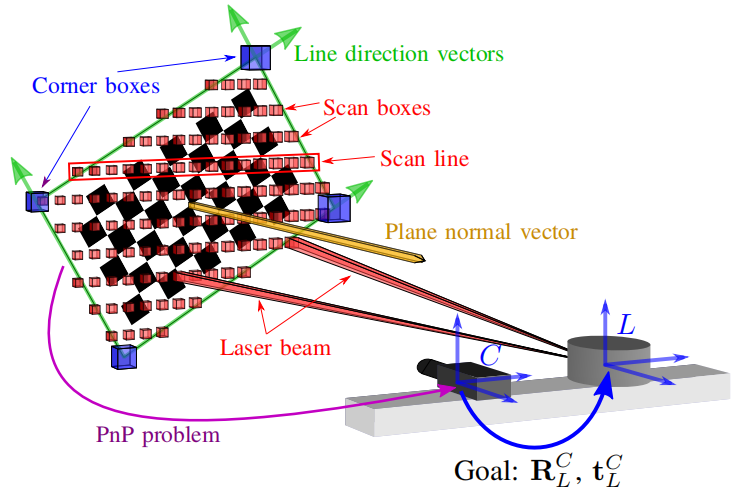
图1：本文的方法概述。为了找到外部校准，如旋转矩阵R和转换向量t，在间距不确定的情况下，相机和3D激光雷达之间寻找点、线、面特征。

传感器误差模型

A.相机模型：

我们采用OpenCV库中包含的方法，用于检测相机图像中的棋盘角。因此，我们使用的原始测量是图像中的像素点。然后，针孔相机模型用于找到指向棋盘角的方向的3D向量。

不能完全检测到角的原因：

相机具有有限的分辨率，因此必须将模拟信号（即实际场景）离散地分为像素；
图像模糊，例如检测对象未处于适当的聚焦；
图像传感器受到损坏，每个像素的各个颜色通道产生了噪声，从而在角检测期间再次导致误差。

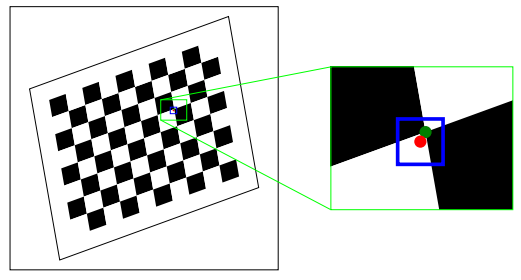
图2：检测到棋盘角（绿色点）的棋盘的示例图。各种误差源导致检测不准确（红色点）。因此，我们应用了我们的界限误差模型，来包裹真实特征的蓝色边框。

B.激光雷达模型：

由于激光雷达的激光光束和表面入射角受到传感器的环境（温度，湿度等）的影响，实际测量通常产生误差。由于无法预测此系统错误，因此无法使用已建立的随机误差模型进行建模。测量点的实际位置是不确定的，并且可以是激光光束扫描的任何位置。因此，选择基于间距的模型来考虑这种不确定性。

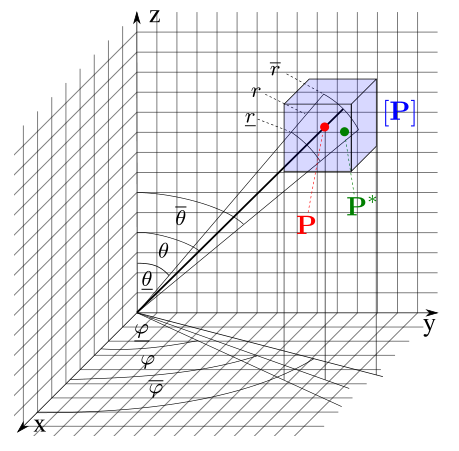
图3：3D盒[P]的可视化由未知但是界面的误差为球形坐标R，θ和φ产生的误差。3D盒可以保证覆盖实际测量的点P *和原始测量的点P。

主要结果

我们使用Gazebo 和实际数据生成的模拟数据来评估我们的方法。此外，将我们的方法与最先进算法进行了比较。然而，直接比较是不合适的，因为他们的方法的目标是找到最好的点值结果（point-valued result），而我们的方法旨在封闭真实的解决方案并同时表明计算的不确定性。

A.仿真数据

选择尺寸为100×76厘米的标定棋盘，其中，棋盘距离多传感器系统大约2.5米。模拟相机的像素误差遵循高斯分布，平均值为0，标准偏差为0.01。这导致相机校准期间0.3 px的最大角度检测误差。模拟3D激光雷达的型号是Velodyne VLP16。球形坐标的误差遵循均匀的分布，无需任何异常值。

首先，我们显示从一个标定棋盘姿态计算的转换参数的结果。如图所示，我们选择六种不同的棋盘姿态，以显示对不同外部校准参数的影响。

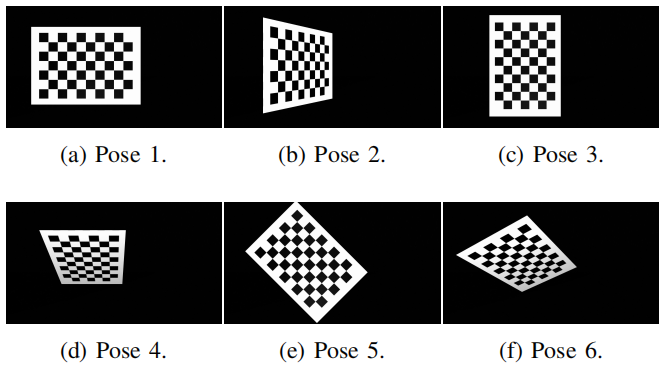
图4：六种不同棋盘姿态的模拟图像。

对于所有六个姿态，我们的方法包含真实的转换参数。然而，转换参数的准确性随着表I中的参数变化。这可以通过标定棋盘的相应姿态来解释。例如，Pose1和Pose5可以通过沿Z轴旋转和平移实现。

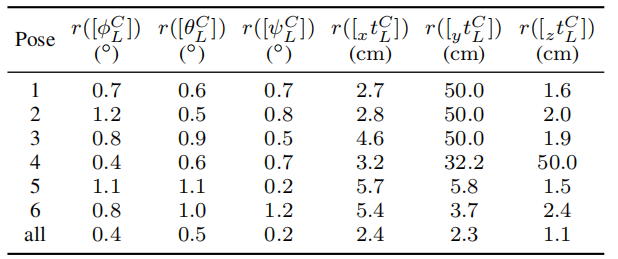
表I：图3中的姿势的间距半径

表II显示了相机和激光扫描仪的不同模拟误差的结果。显然，相应地调整传感器误差界限。例如，第二行示出了用于[Δpx] = [-0.4,0.4] px的间隔半径，而其他传感器误差界限保持不变。作为参考，第一行显示出了上面引入和评估的错误界限的结果。表格可以说明我们的方法可以在增加不确定性的情况下处理相机和激光扫描数据的不同误差。

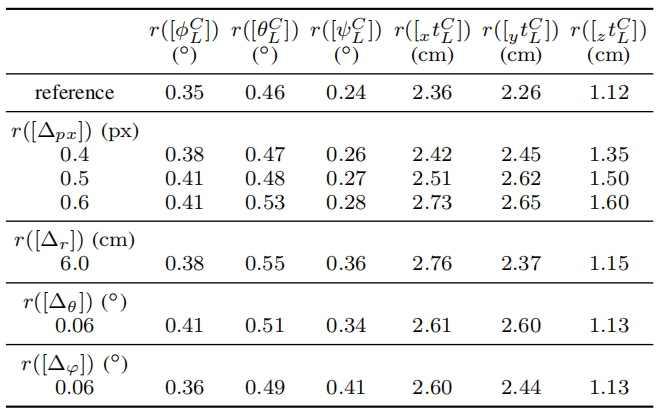
表2：不同模拟误差参数的影响

接下来，展示了系统误差对我们方法的影响。我们使用总共27个棋盘姿态，包括上面所示的六个姿态，在传感器设置周围的旋转空间中均匀分布。

表3：结果显示偏误差测量对我们和最先进的方法的比较

B.真实数据

如图4所示，实验设备包括Velodyne VLP-16 LIDAR，FLIR Grasshopper3相机和100×76cm标定棋盘。相机的分辨率为1920×1200 px。激光雷达LiDAR的垂直角分辨率为2°。此外，LiDAR的旋转速率设定为5Hz，导致水平角分辨率为0.1◦。

图5：用于评估的设备概述。

我们收集了26个不同的棋盘姿势的数据。表IV显示结果。得到的间距结果和仿真结果类似。因此，我们的方法不仅可以使用外在校准并评估其准确性，还可以验证随机方法的结果。

表4：我们和最先进方法的数据结果比较

 End 

声明：部分内容来源于网络，仅供读者学术交流之目的。文章版权归原作者所有。如有不妥，请联系删除。