手把手教你编写傅里叶动画
点击上方“AI算法与图像处理”,选择加"星标"或“置顶”
重磅干货,第一时间送达
来源:编程珠玑
先来看几个比较有艺术性的动画:


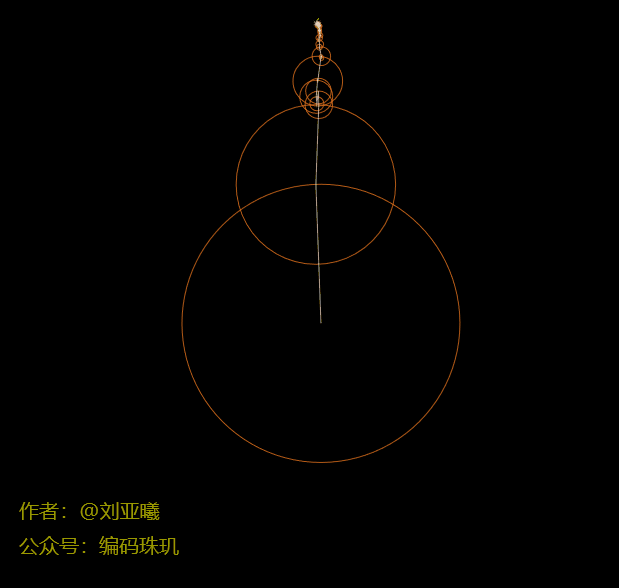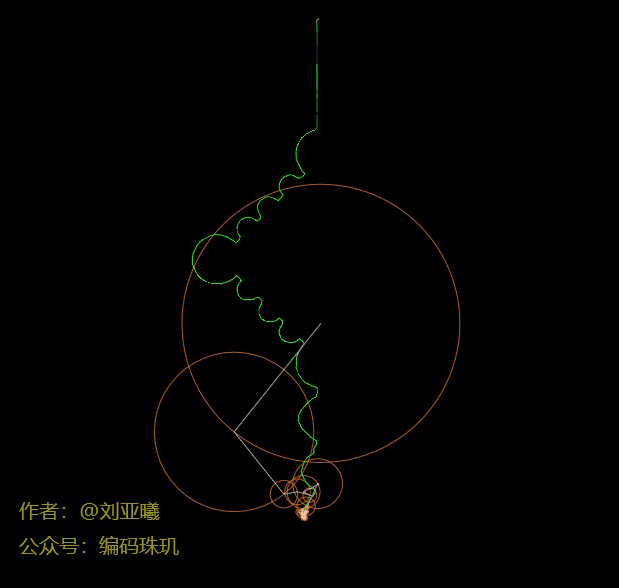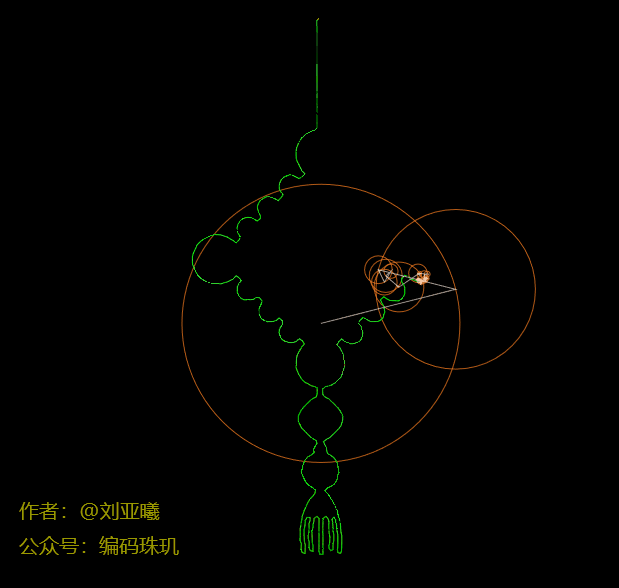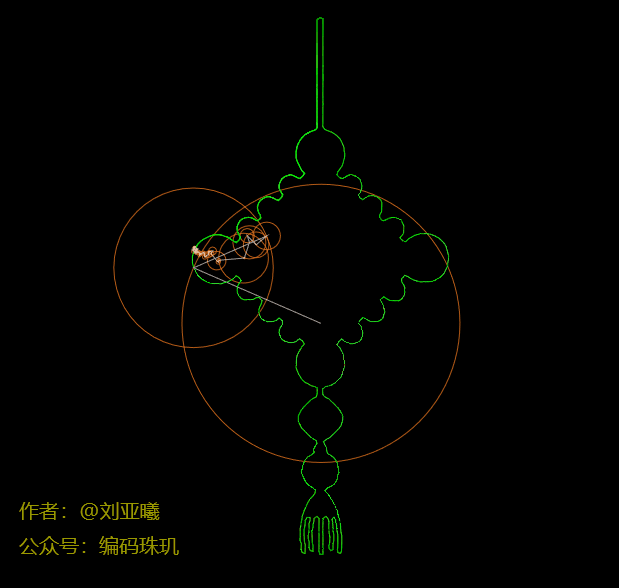
上面三个绘制动画(苹果logo、爱心、中国结)是我用一千个圆,让他们各自按照自己的方向与速度进行滚动,然后把他们首尾进行相连,同时把最后一个圆上某一点的路径记录下来,这便是图中绿色的轮廓。说到这里你有没有感觉:卧槽,怎么做的,我也想做!没关系,这篇文章我会花大量的篇章来介绍这个方法(读者看到动态图可能会有轻微的卡顿,是因为微信公众号限制动态图的帧率,但实际渲染远比这平滑)。
事情先回溯到两百多年前,法国数学家傅里叶提出一个观点:“任何一个连续周期性函数都可以用正弦函数与余弦函数的和来表示”。虽然这句话在当时没有引起重视,但时至今日,我们已经没有任何权利去怀疑这一说辞的分量,因为它的分量已经远远超过当年傅里叶所表达问题的本身。从傅里叶级数衍生出来的傅里叶变换,它的重要性在任何一门工程领域尤其是电子信息领域不言而喻,好不夸张地说,我们每天能够用诸如微信这种即时通讯工具跟好友聊天,除了感谢腾讯外,还应该感谢一下傅里叶同学,因为没有他的那句话,绝对不可能有电子通讯的今天。但是我想相信大部分学过《高等数学》的人对傅里叶变换的概念肯定还停留在只会做题的阶段,并不了解傅里叶变换的本质,而傅里叶变换却是我做图像处理中经常用到的一种算法。所以我写这篇文章的原因就在于想跟大家聊一聊我自己所了解的傅里叶变换,但要说傅里叶变换却绕不开傅里叶级数,所以本篇文章我会主要讲解傅里叶级数,而傅里叶变换在实际工程中的应用例如图像降噪、图像分类、图像压缩等技术,我会在另外一篇篇章中介绍。如果读完本文您觉得对你有用,我希望您能够把它分享出去,让更多的人看到。同时如果你发现有错误,我也希望的到您的指正。另外,我会在本文结尾附带并讲解我编写的傅里叶动画引擎代码,如果你想要的话,请在我公众号的对话框里面回复“傅里叶动画”即可领取,我会把源代码发送给你,方便你后续学习研究。
提到「变换」这个词,想必大家一定不会陌生,没错,我们在大学时候高数里面的变换实在是太多了,诸如拉普拉斯变换、泰勒展开(请参看我上一篇文章泰勒级数有什么用)等等。可是大家有没有想过这个问题:我们们为什么要弄这些千奇百怪的「变换」呢,难道是为了好玩吗?
答案显然不是,之所以我们需要这么多变换,最主要的原因还是我们懒啊,这些变换能使我们把非常复杂的问题简单化,甚至在大多数情况下如果我们不通过这些变换我们的问题是不能解的。
仔细回想一下,其实我们在生活中已经不知不觉地应用了各种变换,例如电子秤并非直接测量实际的体重,而是根据内部压力传感器电阻的变化通过一定的转换来输出实际的数值的。类似的事情,其实在古代已经有了,例如阿基米德通过测量溢出水质量来测量皇冠的密度,曹冲通过石头的重量来测量大象的体重等等,这些都是一种变换。

小曹冲通过测量吃同样水深的石头来测量大象的体重,这也是一种变换
那么我进今天要说的傅里叶变换到底有什么好处呢,换句话说,我们为什么要进行傅里叶变换呢?原因很简单:傅里叶变换能把一个周期性函数分解成多个正余弦函数的叠加,这种变换对我们分析信号有诸多好处,尤其在数字信号处理或者电工学中有重大应用,例如脉冲信号一般都是矩形波,如果我们把它进行傅里叶变换,我们就能看到组成这个矩形波的各谐波的频率、相位、振幅等等,由于正余弦函数的正交性,不仅方便我们计算,而且对我们分析问题带来很大方便。
那么如何理解傅里叶级数呢?如果你你记得公式的话,它是长这样子的:
余弦系数
正弦系数
可这个公式不太完美,过于复杂,而且不能从直观上看出傅里叶公式的奥妙之处,因此我们换种方式,用欧拉公式去化简它,而傅里叶级数的精髓也在这里。但是要引入欧拉公式之前,我们要从虚数说起。
一,虚数的几何意义
虚数
其实虚数的真正含义,代表着旋转:
假如一根数轴上有一个点
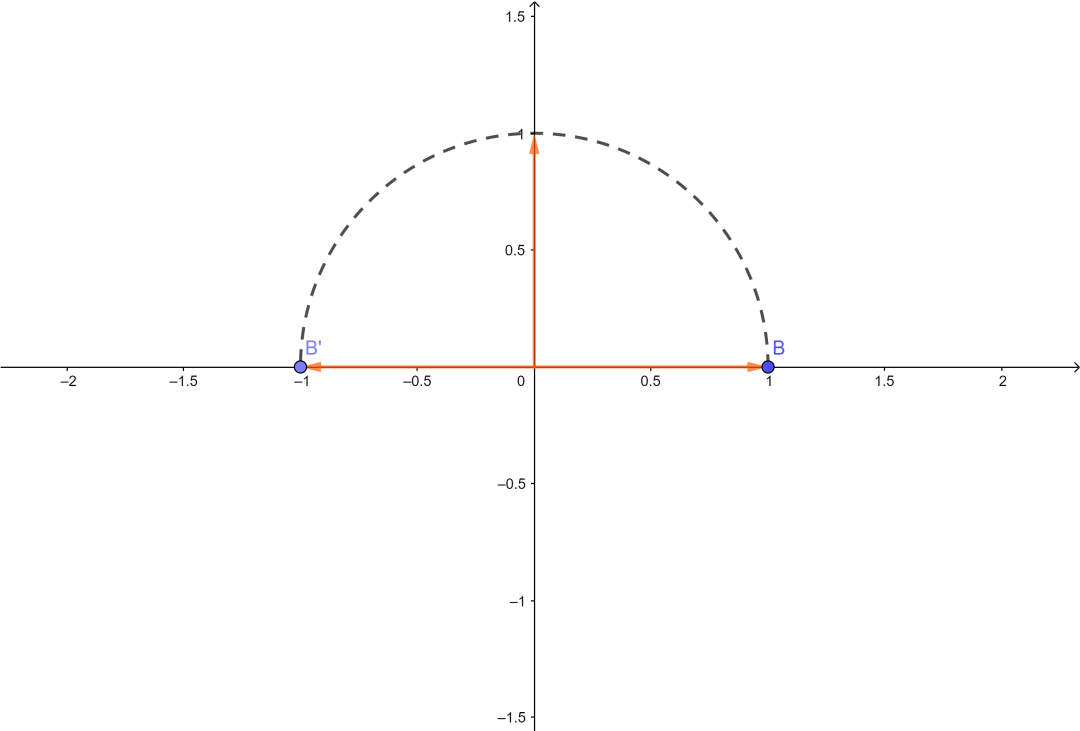
这样我们可以说:
明白了吧,虚数代表一个旋转量,也就是说,只要你看到虚数,就应该想到旋转。
二,复数的几何意义
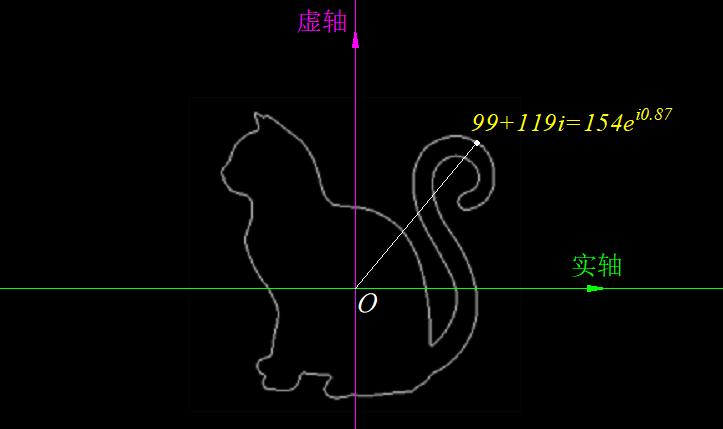
我们进一步拓宽到复数领域,如果把上图中的纵轴表示为虚数轴,横轴代表实数轴,那么任何一个复数
例如如果一个复数
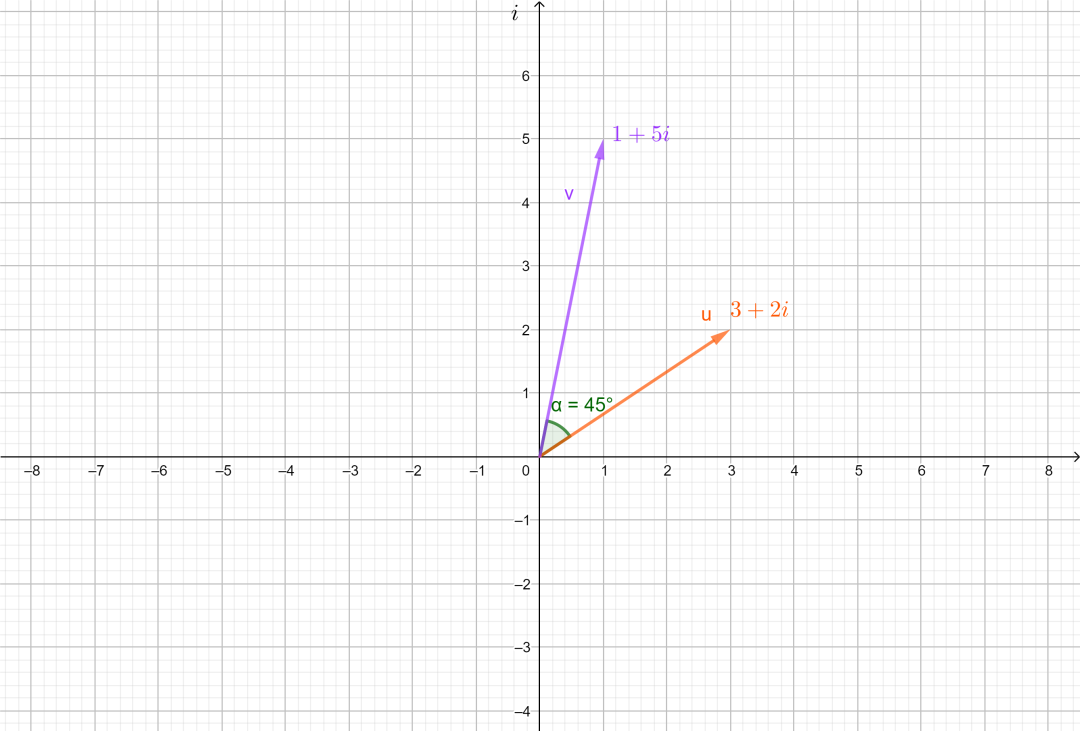
也就是说,对于任意一个复数向量,我们如果想对其进行旋转,那么只需要乘以对应角度的复数即可。这里给出一个简单粗暴的证明方法:
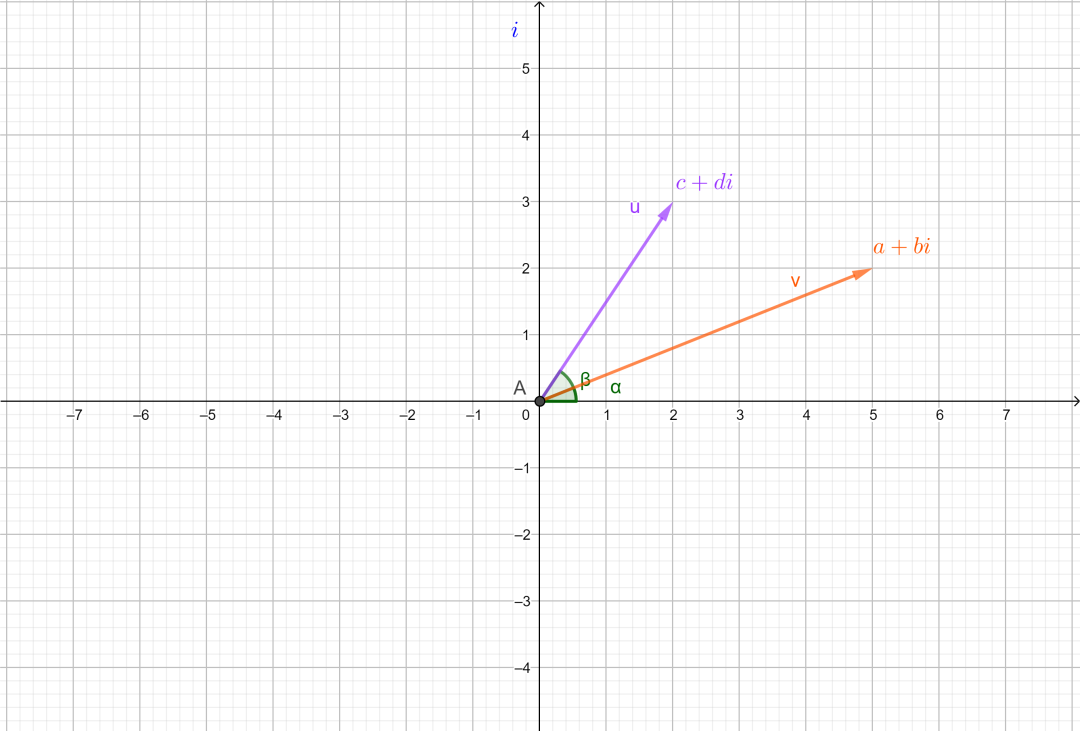
如上图,如果两个向量的长度分别为
利用和差公式化简右边,可得到:
这就说明,两个复数相乘,结果就等于旋转半径相乘、旋转角度相加。
三,欧拉公式的几何意义:一种旋转运动
我们再引入欧拉公式,根据泰勒公式(具体推导过程请参考我另外一篇文章来看看比尔盖茨当年写的BASIC解释器源代码吧,你就知道泰勒级数有什么用了):
由于正弦的泰勒展开为:
余弦泰勒展开为:
将上面两个式子带入
但是不管是欧拉公式还是欧拉恒等式,但凡你第一次看到诸如这种
我们知道,自然底数
为了更加直观理解这一操作,我们再引入复平面单位圆,这里我们先令
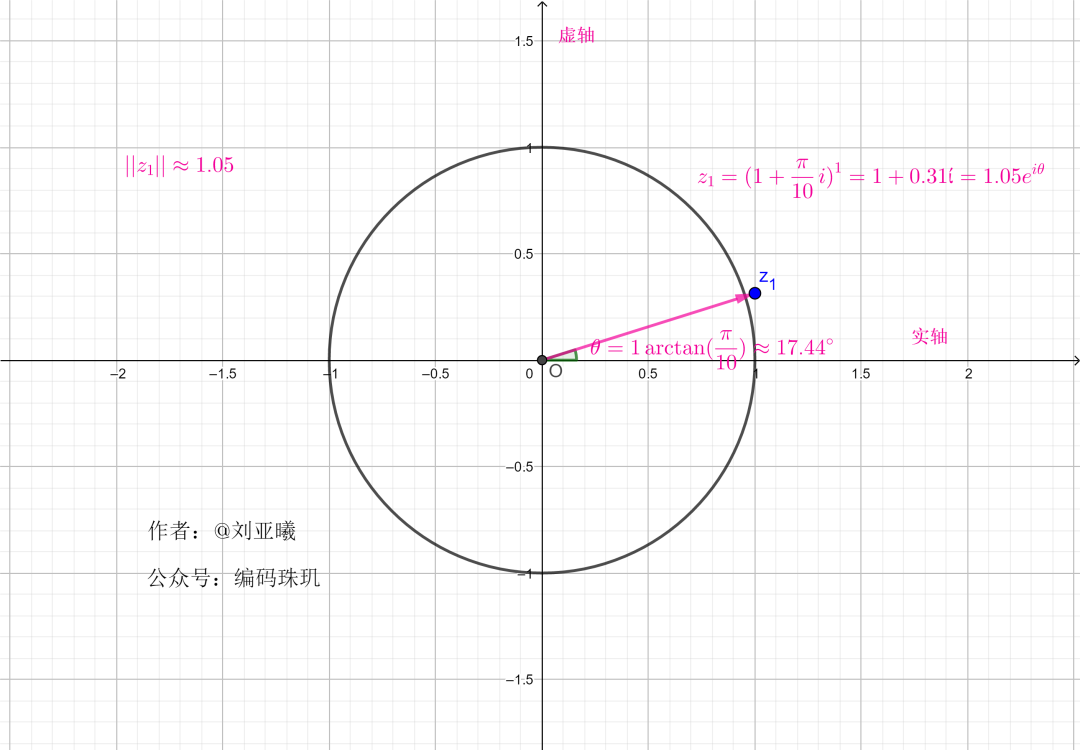
由于连续进行了10次相乘,每次的相乘,都意味着对这个向量进行旋转操作,同进行伸缩。所以10次相乘就是这个向量从原始位置不断旋转,连续十次,每次的角度都为
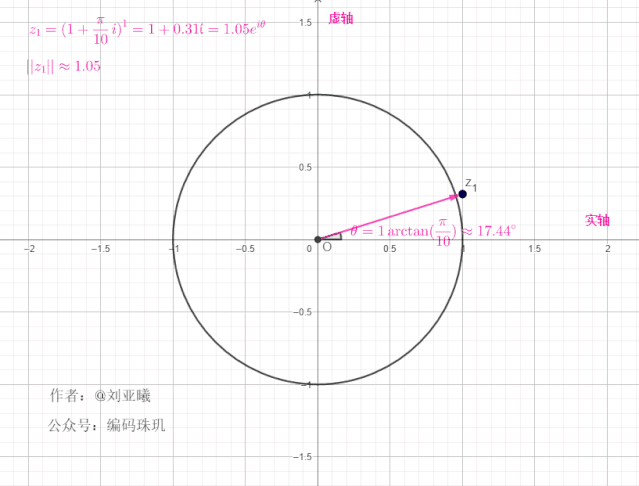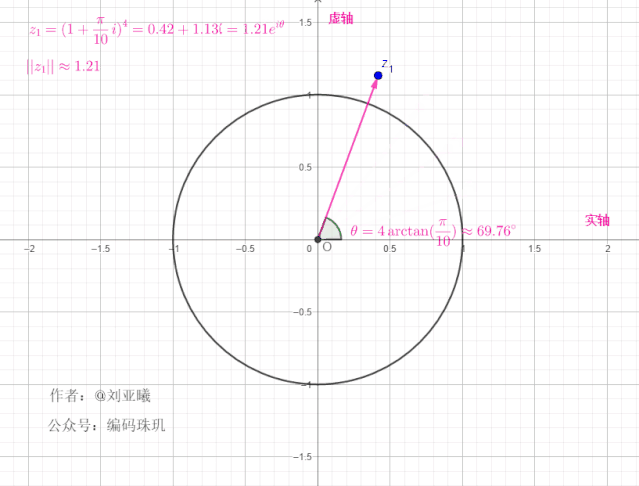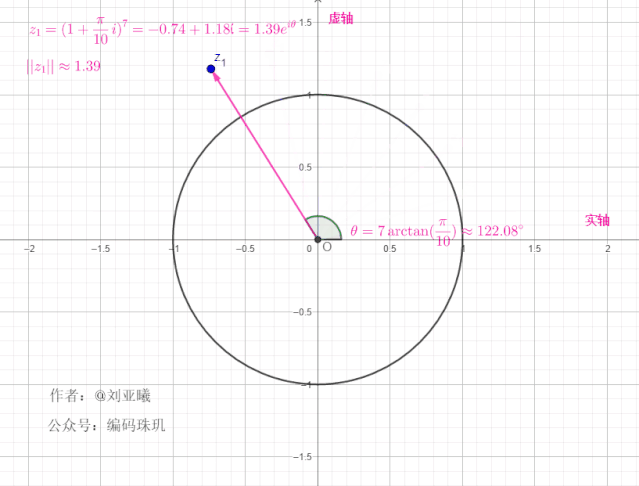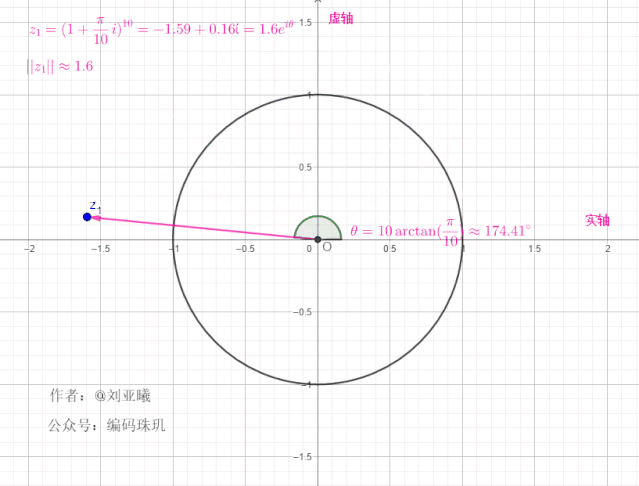
可见,每次经过一次旋转,长度都为上一次的
我们再增大
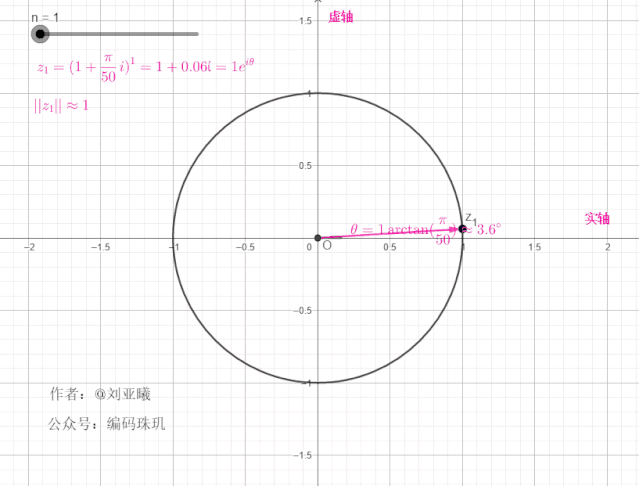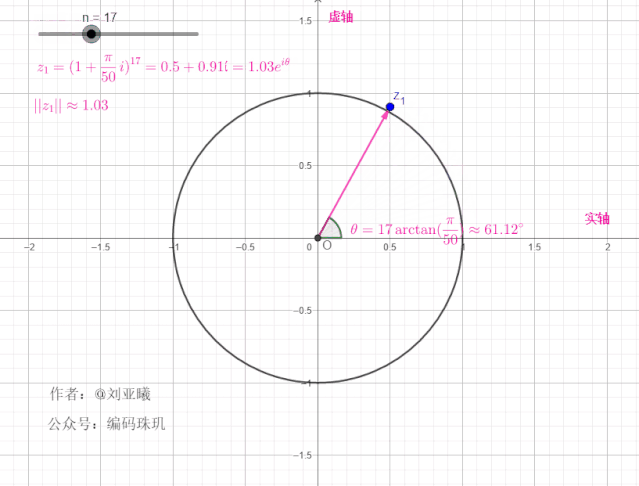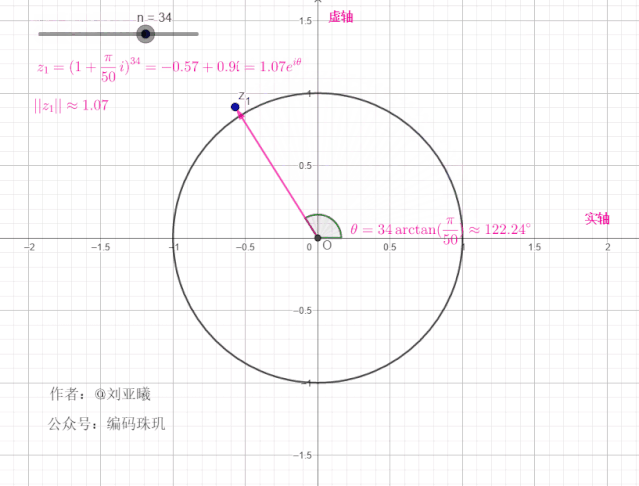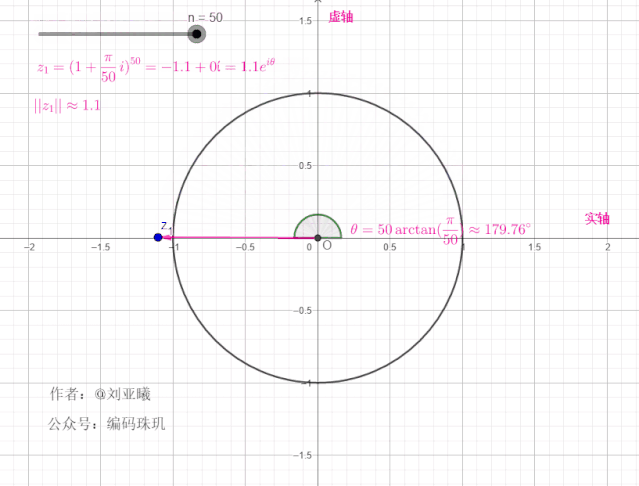
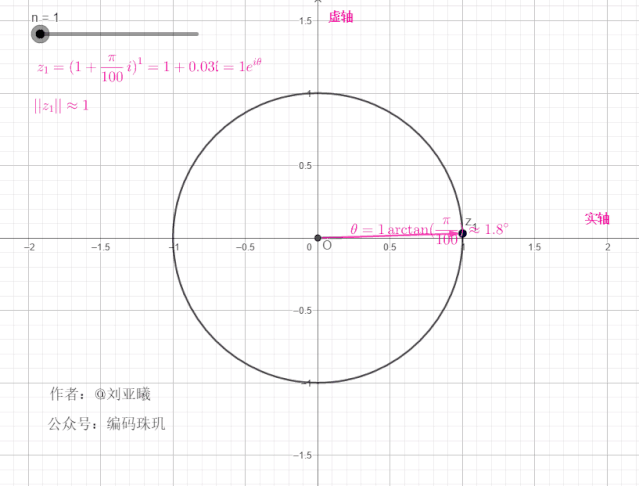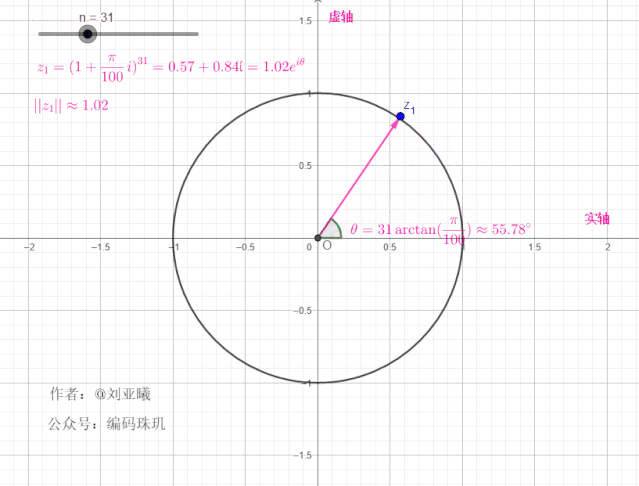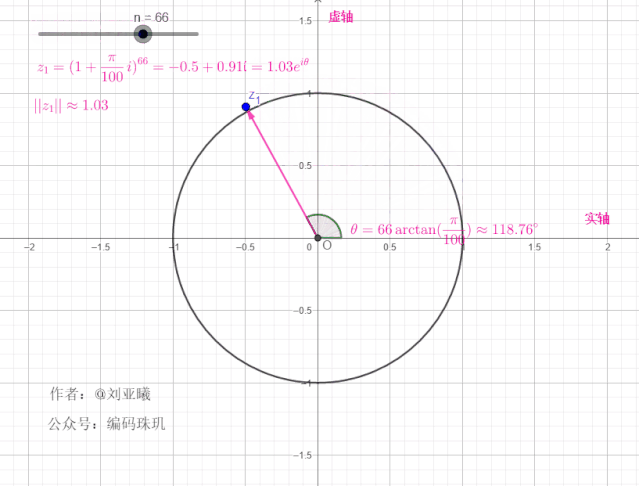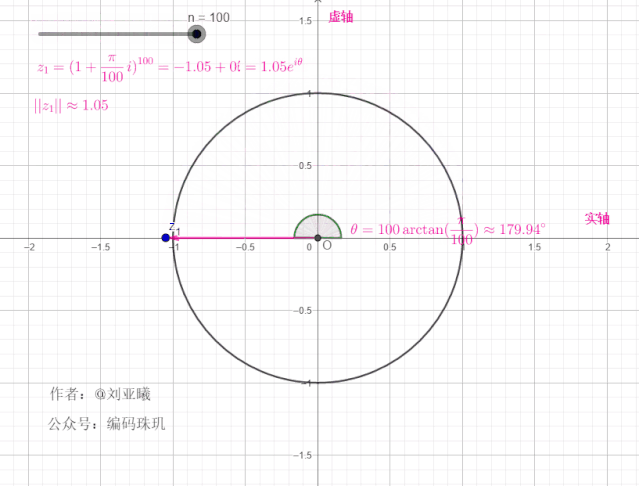
可见,随着
因此,我们得出一个重要结论:
这意味着,如果
我们假设一个复向量的方向为
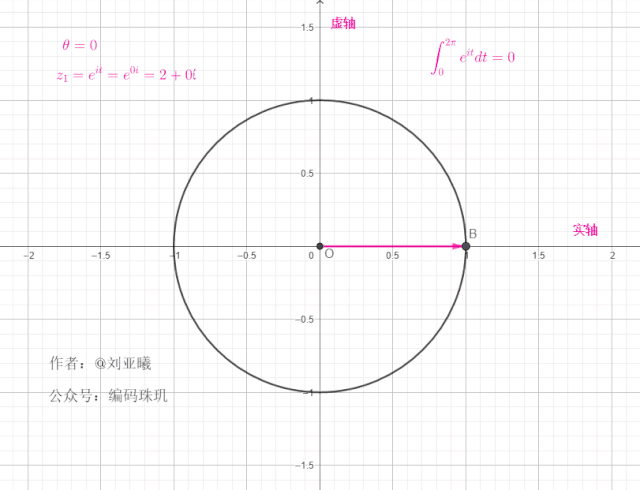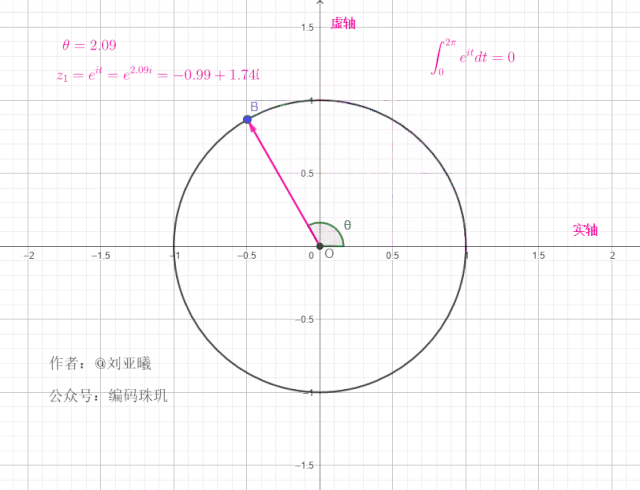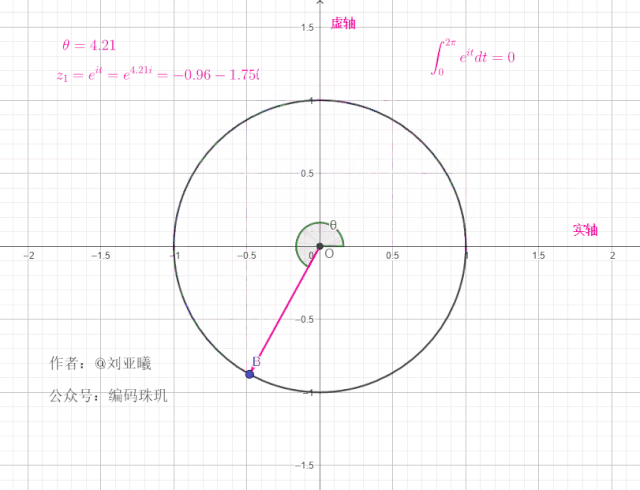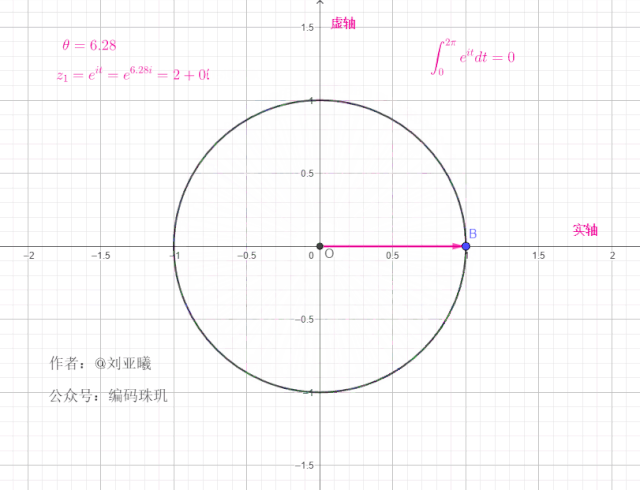
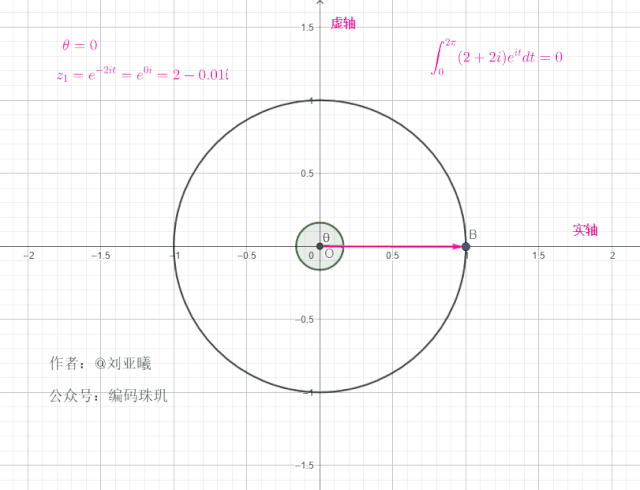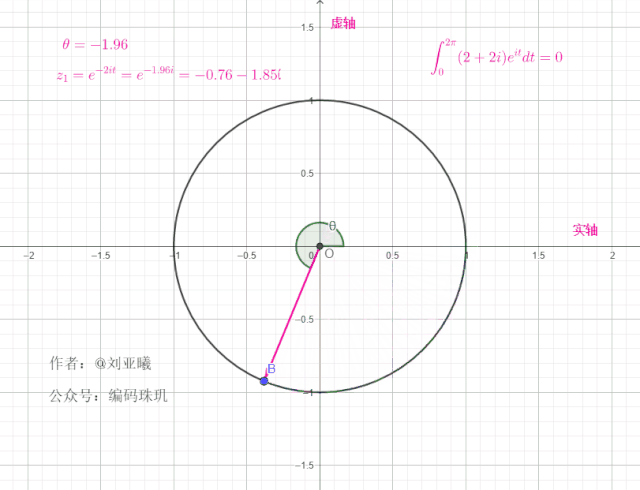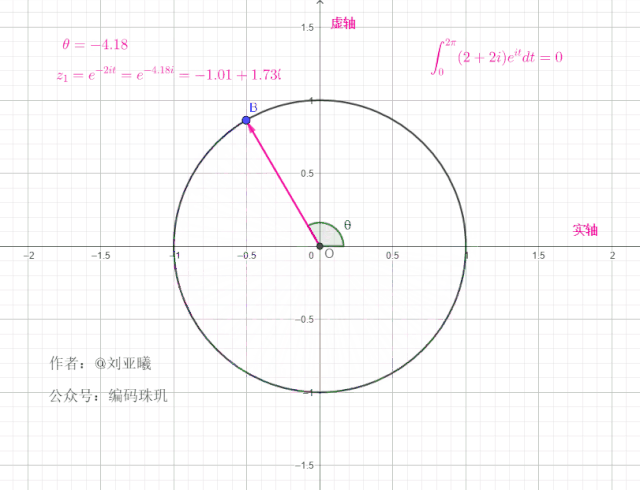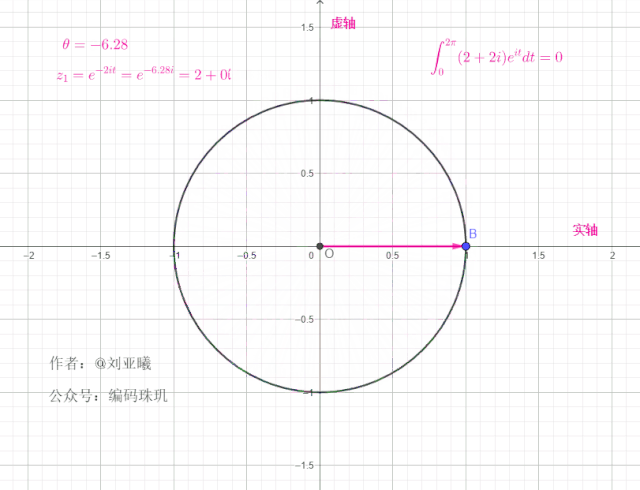
如果初始向量不在1的位置,而是另外一个位置角度,例如初始向量的位置在
初始角度:
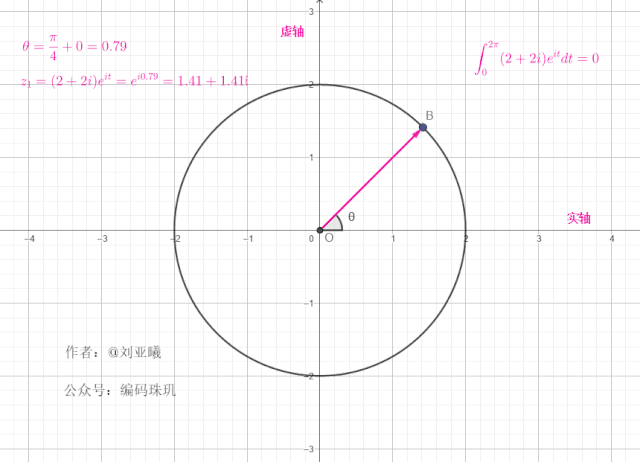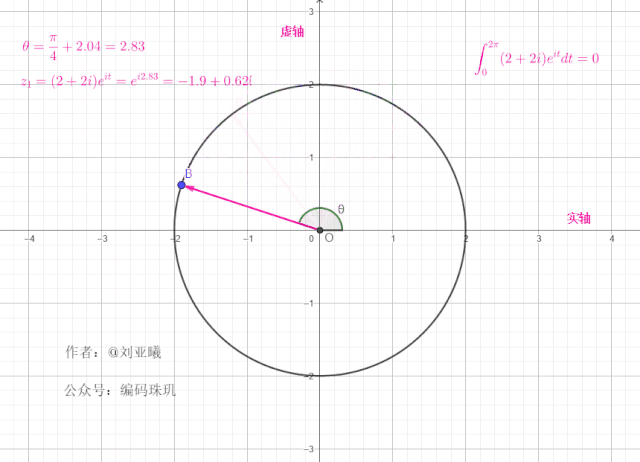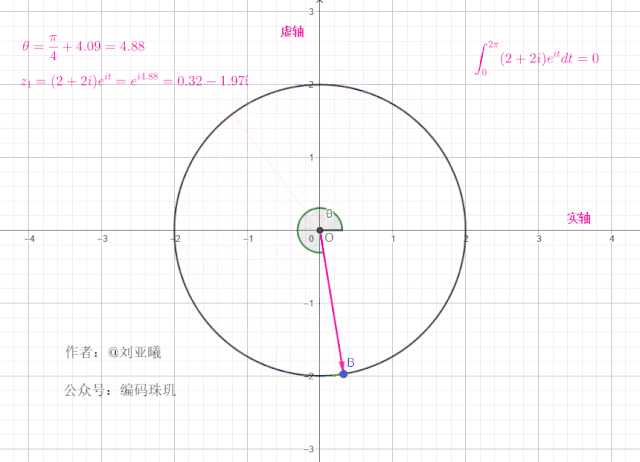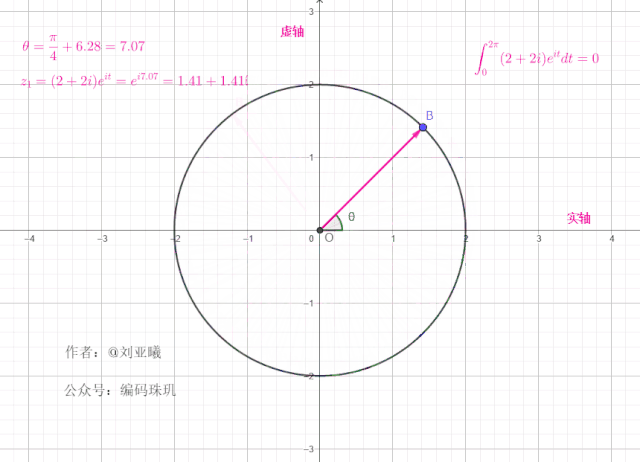
值得注意的是,一个复向量绕单位元旋转一周后,最终位置与初始位置一样,这意味着在任何整个周期区间内,对
这个结论既有趣又重要,它在后面能为我们大大简化计算参数系数的计算量。
而且,根据上面推导出来的欧拉公式:
四,用欧拉公式化简傅里叶级数,窥其本质:
好了,我们利用上面两个正余弦函数的虚数形式,再化简傅里叶级数:
最终,我们得到傅里叶级数的复数形式为:
这种叠加的结果让人觉得不可思议,甚至说恐怖也丝毫不为过,因为只要规定合适的参数,它几乎可以拟合出来我们任何想要的曲线,更神奇的是,有些函数明明带有明显的跳跃不连续点,傅里叶级数居然也能拟合出来,前面我说了方波函数可通过傅里叶级数来获得,即便它带有跳跃点也无所谓:
下面是一个方波函数:我们先用一个圆旋,并记录其某一点纵坐标路径,没错,正弦函数就是这样来的:
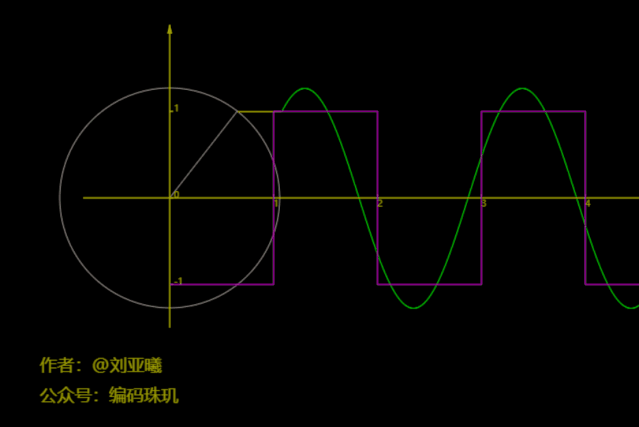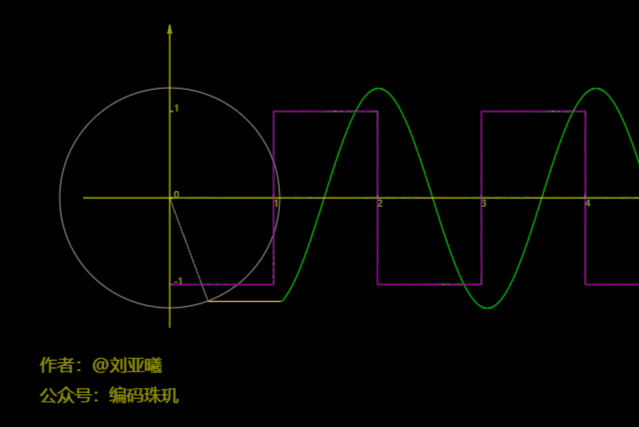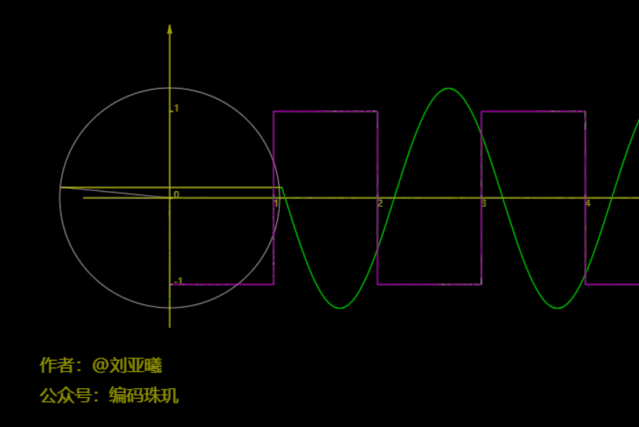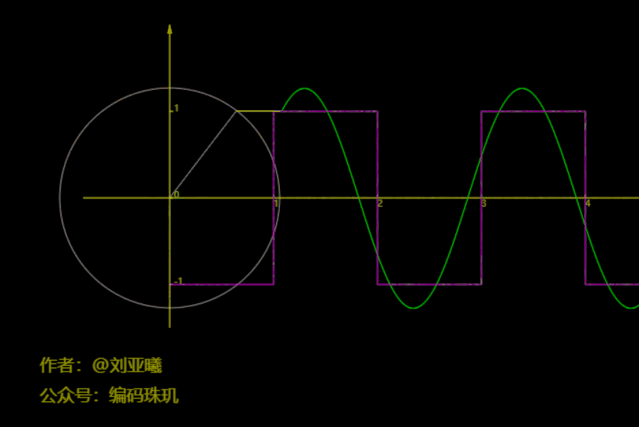
咋一看,有那么几分相似。我们再增加到三个圆:
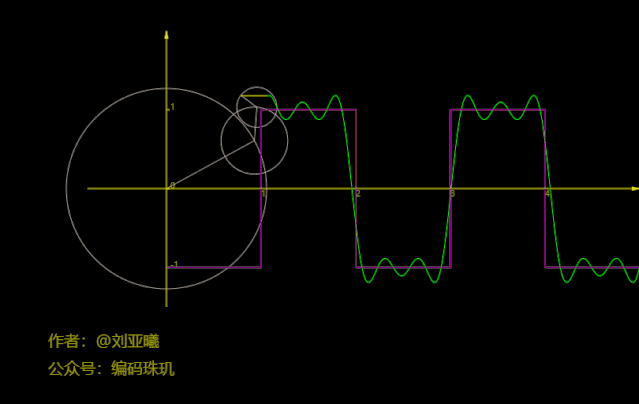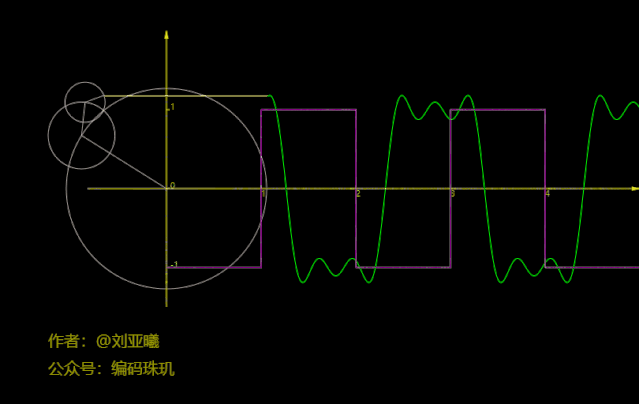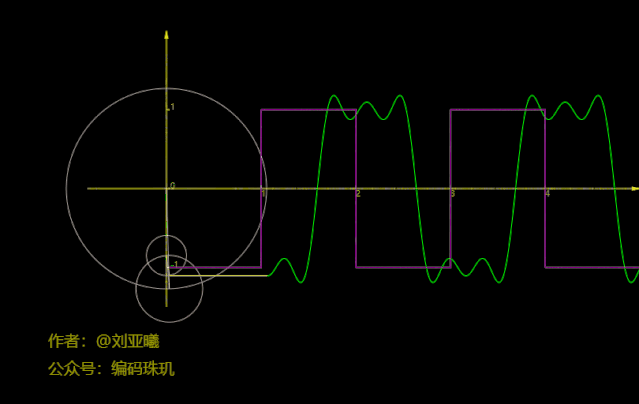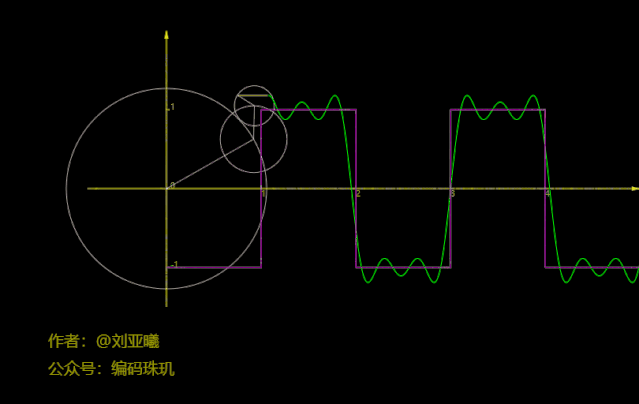
再看,貌似有几分相像了,但还是有差距。
再将圆数量增加到50个:
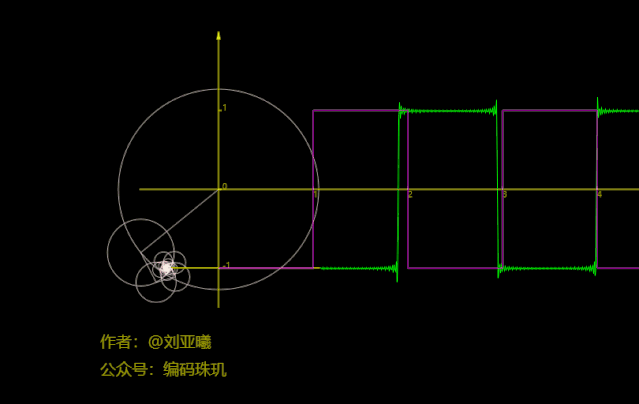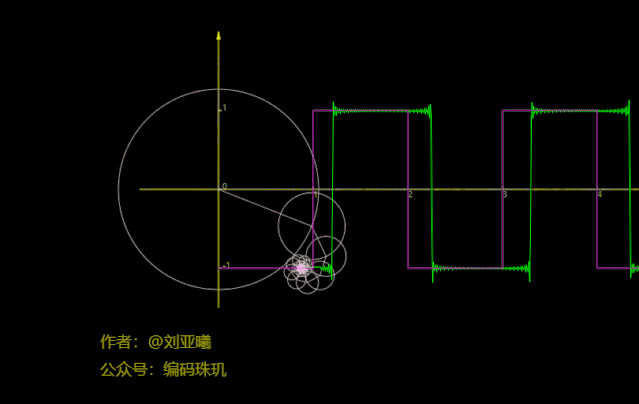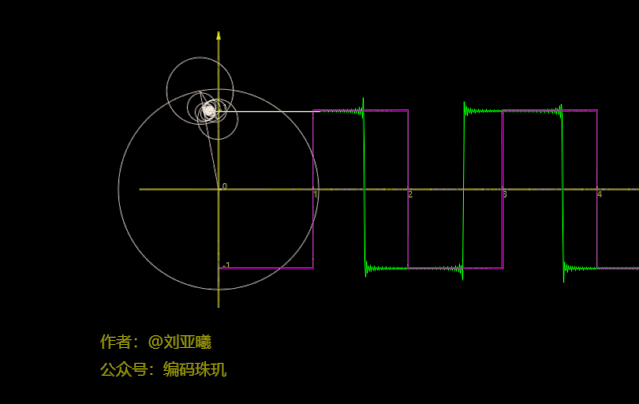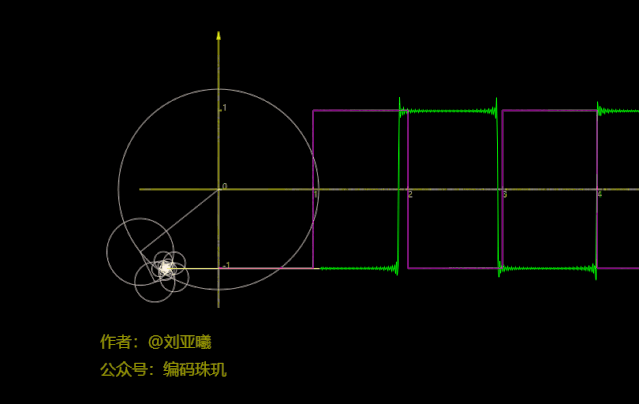
可见,此时方波函数几乎已经与我们的路径拟合在一块了,如果不是你亲眼看到,我相信你很难相信方波函数居然可以通过正余弦函数叠加来近似得到,而更恐怖的是方波的间断点竟然也能拟合出来。并且,随着圆数量的增加,我们拟合的结果会越来越准确。实在是太恐怖了,而且通过合适的圆数量它几乎能拟合出任何你想要的的图像路径。不过要说明的是,上面每个圆的旋转方向与速度都是计算出来的,具体是如何计算的呢,请继续往下看。
五,傅里叶动画的制作。
有了上面的知识,我们做文章开头那几个动画就有思路了。我只是通过计算,把上面一连串的
(1),函数
(2),每个复向量前面的系数
下面我们仔细剖析这两个问题。
5.1,获取
首先来说
1),对图像进行灰度转化;
2),将转化后的灰度图像进行高斯模糊处理,目的是让轮廓更加平滑;
3),再将处理后的图像进行二值化处理,实现黑白分明的轮廓;
4),利用Canny()算子提取轮廓;
5),使用findContours()接口提取图像轮廓坐标数据集合。
根据这个方法,我们几乎可以提取任何图片的轮廓:

c++实现代码如下:
//函数功能:对图像进行轮廓坐标提取//返回值:int//作者:@刘亚曦using namespace cv;using namespace std;int main(){Mat src = imread("自己图片的路径");Mat grayImage;cvtColor(src, grayImage, CV_BGR2GRAY); //灰度处理GaussianBlur(grayImage, grayImage, Size(3, 3), 0, 0); //高斯模糊处理threshold(grayImage, grayImage, 128, 255, CV_THRESH_BINARY); //二值化处理Mat cannyImage;Canny(grayImage, cannyImage, 128, 255, 3); //提取边缘算子vector<vector> contours; vectorhierarchy; //contours为输出的轮廓数据集合findContours(cannyImage, contours, hierarchy, CV_RETR_EXTERNAL, CV_CHAIN_APPROX_NONE, Point(0, 0));return 0;}
这行代码要根据你图片的实际情况来稍微调整几个参数,例如灰度阈值、高斯核半径、canny算子阈值等等。这几个参数在一定程度上决定了你提取图片轮廓的质量。不过在这里这几个参数暂时不做重点讲解,等我有时间会在另外一篇文章中专门讲解一下几种边缘检测算法与参数的意义。大家按照我上面代码里面的参数设置即可,基本上能适应大多数图像了。
这样,我们就能得到我想所要的图片轮廓坐标集合,上面代码中,contours参数就是储存输出值。而且这里有趣的是,它提取的图片轮廓像素坐标是有一定顺序的,一般是以逆时针排列的,这对我们后面处理积分运算极大方便。这就是
5.2,计算
那么究竟如何计算
两边再次积分,注意,再根据上面的结论,上式除了
5.3,动画引擎代码的编写与实现:
其实这个框架非常简单,我们首先根据上面推导出来的公式,由于
代码部分:
在计算过程中,我们要不断计算复数的相加,复数的相乘等方法,所以我们先封装几个常用的工具函数方便我们后面调用,我们返回值都为一个长度为2的数组,第一个代表实部值,第二个值代表虚部。实现代码如下:
//返回类型:[]//作者:@刘亚曦//功能:指数转化为复数function exp(theta) {return [Math.cos(theta), Math.sin(theta)];}//功能:两个复数相乘function mul(za, zb) {return [za[0] * zb[0] - za[1] * zb[1], za[0] * zb[1] + za[1] * zb[0]];}//功能:两个复数相加function add(za, zb) {return [za[0] + zb[0], za[1] + zb[1]];}
我们再定义一个数组
//功能:储存下标值//作者:@刘亚曦//返回值:[]var circleCount = 1000; //圆的数量var K = [];for (var i = 0; i < circleCount; i++) {K[i] = (1 + i >> 1) * (i & 1 ? -1 : 1);}
然后我们开始计算
我们再定义一个getCn()函数,来计算
//函数功能:穷举法计算复向量系数c_n//返回值:[]//作者:@刘亚曦function getCn() {var z = [0, 0];var N = path.length; //路径坐标数组for (var j = 0; j < K.length; j++) {for (var i = 0; i < N; i++) {var za = [path[i][0], path[i][1]]; //f(t)var zb = exp(K[j] * i * 2 * -Math.PI / N); //调用指数转复数函数z = add(z, mul(za, zb)); //调用相乘函数}z[0] = z[0] / N;z[1] = z[1] / N;Cn[j] = [z[0], z[1]];}}
至此,我们就将全部的所需要的
最后 ,我们定义三个绘画函数,用来绘制我们的圆、路径、以及连接圆心的直线,在主函数里面循环刷新,即可形成动画。其实这三个函数非常简单,前面我们的
//功能:画圆函数//作者:@刘亚曦//返回值:voidfunction DrawCircles() {let p = [center_x, center_y];var a = 2 * Math.PI * time / path.length;for (var i = 0; i < Cn.length; i++) {context.beginPath();var r = Math.hypot(Cn[i][0], Cn[i][1]);context.arc(p[0], p[1], r, 0, 2 * Math.PI);context.lineWidth = 1.0;context.strokeStyle = "rgba(255,128,32,0.7)";if (i > 0) {context.stroke(); //第一个圆不画}p = add(p, mul(Cn[i], exp(a * K[i])));}}
再定义绘制路径函数,这个几乎跟上面画圆函数没有区别,因为我们已经计算出来了圆心的实时坐标,直接将他们连起来即可:
//绘制连接圆心函数//作者:@刘亚曦//返回值:voidfunction DrawLines() {context.beginPath();let p = [center_x, center_y];var a = 2 * Math.PI * time / path.length;for (var i = 0; i < Cn.length; i++) {if (i == 1) {context.moveTo(p[0], p[1]); //第一个线不画}p = add(p, mul(Cn[i], exp(a * K[i])))context.lineTo(p[0], p[1]);}context.lineWidth = 1;context.strokeStyle = "rgba(255,255,255,0.6)";context.stroke();}
最后,来绘制路径函数。这个函数比较特殊,我重点说明一下。这里的路径指的是最后一个圆上面一个点的实时坐标,具体是哪一点呢,这是由最后一个圆对应的
//功能:绘制路径函数//作者:@刘亚曦//返回值:voidfunction DrawPath() {let p = [center_x, center_y];var a = 2 * Math.PI * time / path.length;for (var i = 0; i < Cn.length; i++) {p = add(p, mul(Cn[i], exp(a * K[i])));}var x = p[0];var y = p[1];valuePointer++;values_x[valuePointer & pointCount] = x;values_y[valuePointer & pointCount] = y;context.beginPath();context.strokeStyle = "rgba(0,255,0,1)";context.moveTo(x, y);for (var i = 1; i <= pointCount; ++i) {context.lineTo(values_x[(valuePointer - i) & pointCount], values_y[(valuePointer - i) & pointCount]);}context.stroke();}
注意,上面的代码我都跳过了第一个圆的绘制,读者看到的圆是加上是少了一个的。为什么要这样呢?这是因为
上面几个函数都封装好了,剩下的就更简单了,我们在主循环函数里面不断去调用它实时刷新屏幕即可,代码如下:
//循环刷新函数//作者@刘亚曦(function frame() {context.clearRect(0, 0, canvas.width, canvas.height);context.fillStyle = "#000000";context.fillRect(0, 0, canvas.width, canvas.height);DrawCircles();DrawPath();DrawLines();time = time + 2;window.requestAnimationFrame(frame);})();
最后,我们根据上面提取出来的轮廓,我们来试运行一下。我们不断调整circleCount参数,首先我们用5个圆来运动,乍一看,不知道这画的是什么:

再用50个,circleCount=50:
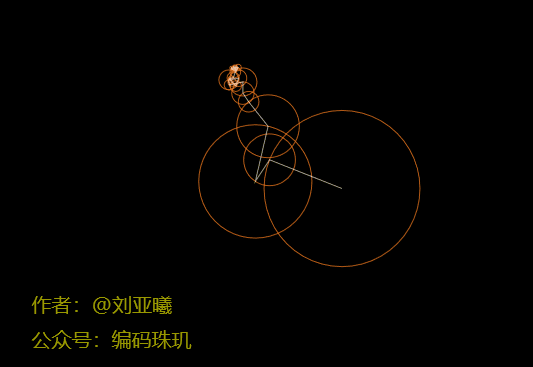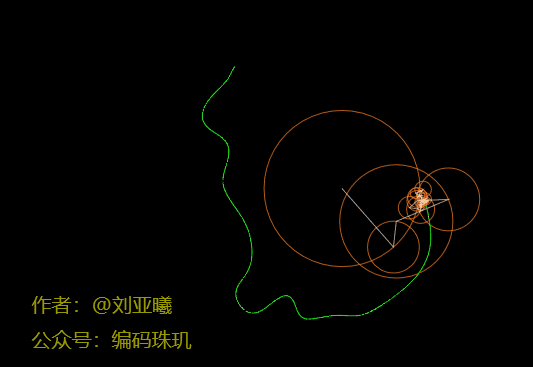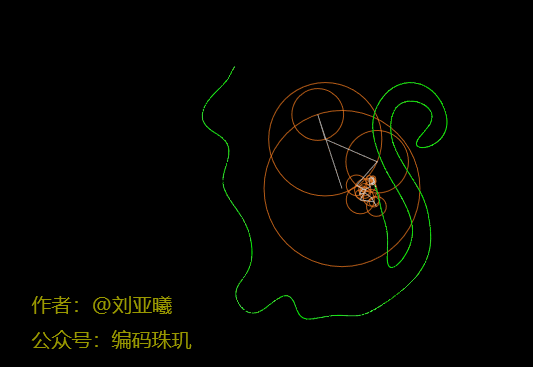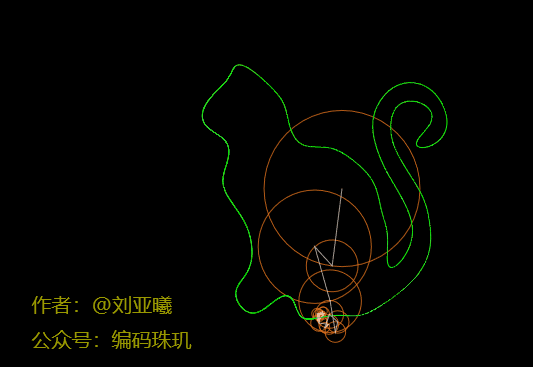
这个轮廓我们已经能够看出是什么了,但是细节不太完美。我们再增加到500个,circleCount=500
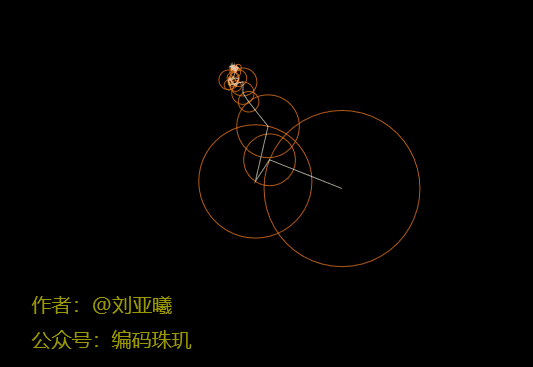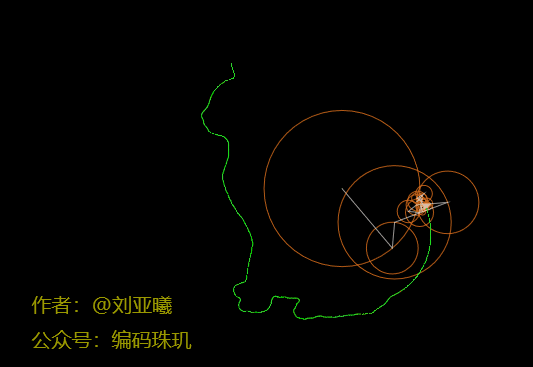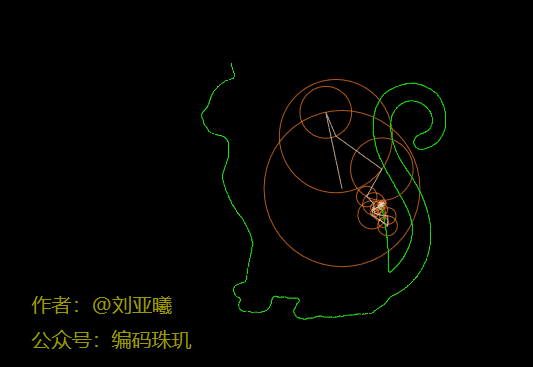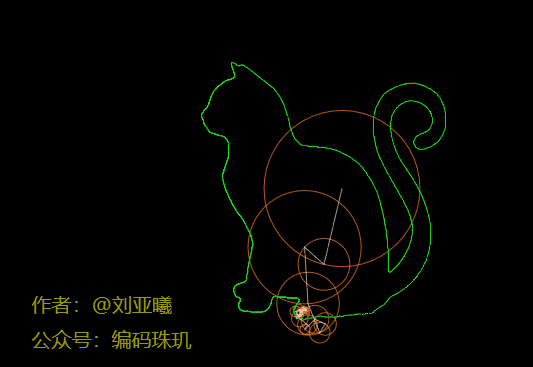
可见随着圆数量的不断增加,最后一个圆的运行轨迹会越来越接近我们所需要的轮廓路径。
六,结语:
说到这里,本文就算结束了。我在这篇文章中把主要的篇章放在了傅里叶级数的推导过程中,尤其是欧拉公式的理解应用,我相信,只要你能够理解上面的数学原理,那么写代码对你来说就是体力活了。由于篇幅长度的限制,代码我没有附带完整,但是读者如果想要完整的动画引擎代码的话,可以扫描下方的二维码,关注我的公众号,在对话框回复“傅里叶动画”五个字即可,我会把完整源代码与素材都发送给你,方便你后期学习研究。如果你觉得本文对你有帮助,我希望你能够点击左下角的分享或者在看按钮,让更多的人看到。另外,由于我的公众号不支持留言功能,如果你有什么疑问或者建议的话,可以在对话框里面给我发私信,也可到我的GitHub博客上给我留言,或者也可以加我个人微信我们一块交流。关于傅里叶变换的实际工程应用尤其是在图像处理方面的重大应用,我会在下一篇文章中详细说明。敬请期待,感谢大家的支持!
扫描下方的二维码,关注我的公众号,回复“傅里叶动画”五个字即可领取本文完整源代码:
