通俗篇：一文搞定矩阵相关概念及意义
点击上方“小白学视觉”，选择加"星标"或“置顶”
重磅干货，第一时间送达
本文转自 | 深度学习这件小事
最近在学习矩阵相关知识，但是其抽象的解释让人摸不着头脑，通过浏览一些博客的内容和自己的理解，本文通过通俗的语言将矩阵的内涵做了总结。其中除了书本和个人观点，部分引用博客。本文主要帮助大家理解矩阵，但不一定都是正确的，但愿能起到促进学习的作用。
正式开始之前，我们需要明确一些事情，什么是问题的实质，什么是解决问题的工具。比如相似矩阵，相似是一类问题的实质，虽然两个矩阵相似，但是我们通过矩阵并不能清楚看出他们的特点作用，于是我们引入对角化这个工具，将n阶矩阵通过对角化转成对角矩阵便于运算和理解。本文只讲思想，不测重计算，所以举例皆为3阶及以下矩阵。
第一节
矩阵这么多的应用是有一个前提条件的，那就是这个矩阵是位于线性空间当中的。本节主要讲述什么是线性空间，以及一些基本的规定（概念）。
线性空间（又称向量空间）和子线性空间。
书本概念:线性空间是满足……的一个封闭空间。线性子空间是在满足上述特点的同时还要是父空间（自定义概念，便于理解）的子集。那什么是线性空间?我们怎么才能从线性空间中分割一个子线性空间出来呢。举个很简单的例子：
我们以三维空间T为例，它的x,y,z轴坐标分别从负无穷到正无穷。根据以往的经验很显然，它是一个封闭的空间，而且满足线性空间的特点，所以它肯定是一个线性空间。现在我去掉它的一个维度，比如让Z=常数，这时候我们得到一个二维空间S，空间S实际上只包含x,y两个维度，根据以往的经验，很容易知道它也是一个线性空间，因此S也是T的子线性空间。同理我们再去掉一个维度，让空间变成一维空间。这些也是成立的。
特殊的向量空间。
欧式空间：简单理解为可以用长度角度等来度量的线性空间，带有内积的空间（内积可以理解为投影，是空间可以度量的一种表现形式，我们通过长度和夹角来求内积，也可以反过来用内积表示长度和大小）高中几何的空间就是欧式空间。
酉空间：一种特殊的带有正定埃尔米特型的复内积空间V（非完备内积空间），可以进行与欧式空间类似的度量，度量工具如：范数（范数：简单理解为向量的长度，到0点的距离，将向量空间对象进行欧式空间的描述，简化理解）。
希尔伯特空间:完备的内积空间。
完备性：其中完备性的意思就是空间中的极限运算不能跑出该空间，如有理数空间中的√2 的小数表示，其极限随着小数位数的增加收敛到√2，但√2 属于无理数，并不在有理数空间。
关于空间的推导递进关系可以参考博客：
http://blog.csdn.net/shijing_0214/article/details/51052208
理解：现在我们学习的空间是对我们生活中常用的欧式欧式空间的一个抽象提升，比如距离长度对应抽象提升为范数，角度的表示抽象成内积相关，理解简化学习难度。
空间的维数，基与坐标。
在这门学科中，空间的物体都是由向量或者向量的组合进行表示。在之前的数学中，我们使用的坐标系是固定的，为了简化，我们规定坐标系后就忽略了基向量，但现在因为坐标系不在固定（个人觉这是因为，矩阵中使用的空间是一种广义的空间，所有的物体都包含在该空间内，没有人可以跳出这个空间来规定哪里是基向量，我们都是处于空间中不同的角度来观察这个空间，这样我们必须同时使用所处的相对坐标系和相对坐标来描述空间的物体，这种空间在某种意义上涵盖更为广泛，更加贴近对现实的客观描述），我们描述一个物体时就要同时表明他的坐标系（基向量的组合）和坐标。
基向量相当于每个维度的单位向量，我们用向量或者向量的组合表示的物体可以整理为坐标+基向量，例如在基向量x,y,z.构成的空间中，我们有一个点O,我们有三个方向的向量表示该点：a,b,c。那么我们也可以说是在以x,y,z为基向量的空间中，点O的坐标为：(|a|/|x|,|b|/|y|,|c|/|z|)。
这几个概念都非常简单，后面章节有用到的会相应的说明。
第二节
这一节主要讲矩阵的线性变换，这些变换是整个线代的基础重点，弄懂了这些东西的实际物理意义将会大大帮助后面的学习和理解。
什么是线性变换（这是一种规定性质，很容易理解这里不做解释）？线性变换可以用一个矩阵来描述，所以矩阵的本质是一个变换，矩阵的乘法就是将这个变换施加给被乘的对象（可以是单点对象也可以是多点对象，单点对应一个向量，多点对应一个矩阵）。这么说可能不太具体，你可能还有疑问说，左乘和右乘的结果为啥不一样？我们举个简单的例子来证明这个观点。
先看一般情况，普通空间中，我们通过旋转，缩放来描述一个物体的变换。下面是三维空间下的旋转矩阵，我们可以尝试将其放在右面去乘一个向量点，我们发现点会绕规定的坐标旋转，但是尺寸没有发生变化，因为这些旋转因子的行列式为1，使得旋转不会影响尺寸的变化。
矩阵在三个方向的旋转因子：
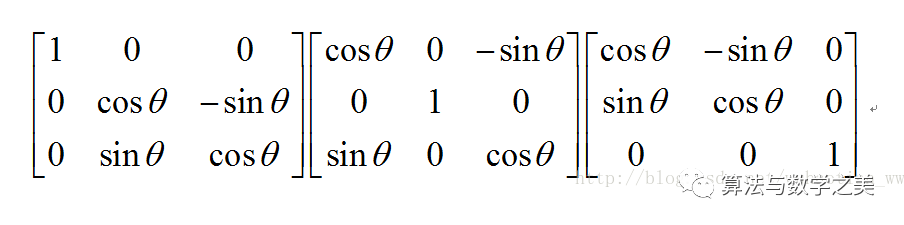
矩阵的缩放因子：
矩阵三个方向的平移因子：
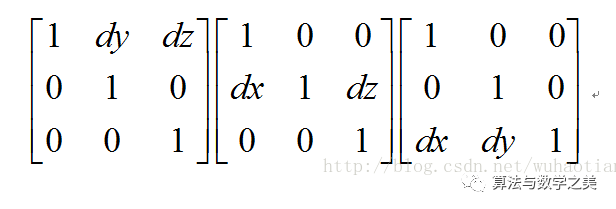
关于这三种变换可以看博客：
http://blog.csdn.net/leaf6094189/article/details/18554549
说完右乘，我们看一下左乘，由于矩阵运算的特殊性，A*B != B*A。我们引入一个工具来使其相等，这个工具就是转置。将一个右乘的矩阵公式按照一定规律改变一下位置就可以实现左乘。如下：
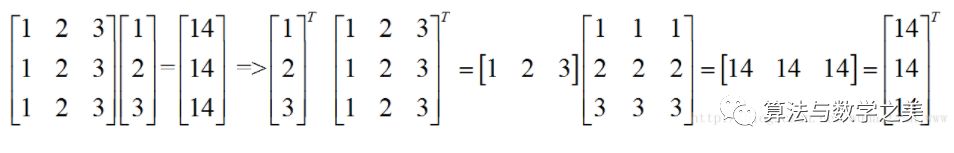
这样我们就很容易的实现左右乘的转换。
有了以上对变化的理解，我们还是会有疑问，一个看起来毫无规律的矩阵我们怎么知道他描述了怎样的变化？对于一个普通的矩阵我们确实无法直观的看出它描述了怎样的变化，我们需要先将普通矩阵进行等价变换（初等变换），然后根据旋转，缩放，平移的因子矩阵，就可以看出这个矩阵的具体含义。比如对于单纯的缩放矩阵，它可以变换成对角矩阵，这样我们很容易看出它的缩放因子。比如对于单纯的平移矩阵，我们可以将它变换成初等矩阵，这样我们很容易看出它的平移关系。对于旋转来说变换较为麻烦，但是原理相似，看官可以自行推导。
上面使用了一种变换工具，初等变换。通过上面的例子，相信我们就不难理解，书本上为什么要花费不少篇幅来讲解初等变换和初等矩阵了。
矩阵为什么支持分块计算？我们该怎么分块。
先从简单的划分开始:
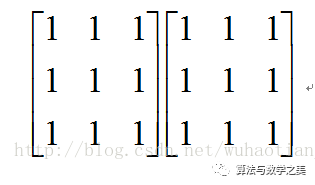
（1）我们把左边的矩阵当作变换矩阵，那么右边的矩阵就相当于待变换点的组合，无论是一个还是两个都不影响计算结果，所以右边矩阵的任意行划分都不影响结果。
（2）我们把右边的矩阵当作变换矩阵，那么左边的矩阵就相当于待变换点的组合，无论是一个还是两个都不影响计算结果，所以左边矩阵的任意列划分都不影响结果。
接下来看左矩阵的列划分和右矩阵的行划分。
从网上找了个例题：要想能使用矩阵乘法计算，我们必须把A的列每段划分的个数与B行每段划分的个数相同，这个不难理解。现在我们忽略掉矩阵中的0元素，将其当作普通元素处理。那么我们会得到下面的式子：
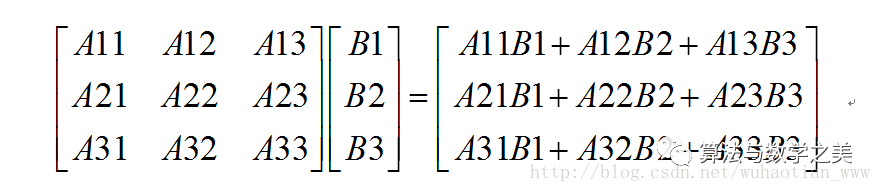
不难看出计算结果和不分块时完全一样，只是简单的拆分组合。究其原因我们可以将其理解为在满足划分特点的情况下，分块计算就相当于对某个或某几个维度分量进行计算，然后求和的过程。
综合上面几条，满足上面特点的任何划分都是成立的。
逆矩阵：AA-1 =E;
目前先了解逆矩阵相当于矩阵的倒数，两者相乘等于单位矩阵。它有很多特点，后面使用到了会继续解释，比如非奇异矩阵行列式，|A|=1/|A-1|.等等。如果从倒数的角度出发就很容易理解。
第三节：行列式与秩
为了描述行列式的意义，我们自己引入一个概念叫做维度积，举例理解一下，二维维度积表示面积，三维维度积叫做体积，对于高维我们将其抽象为维度积。有了这个概念之后，我们发现，行列式的代数结果表示的正是矩阵向量所围成的这种维度积。
关于这个的证明是一项不小的工作量，前人已经证明过了，这里贴出博客：
http://blog.csdn.net/vernice/article/details/48512203
由上面的行列式的几何含义，我们可以推断出什么是奇异矩阵，奇异矩阵就是维度积为0的矩阵（方阵），当方阵中向量不全部线性无关时，维度积为0，比如不完全线性相关的二维方阵表示一条直线，它的二维维度积（面积）为0，比如不完全线性相关的三维方阵表示一条直线或一个平面，它的三维维度积（体积）为0。
所以行列式只有对非奇异矩阵成立，且det(A)=1/det(A-1)。A-1就是定义了A的逆变换，是矩阵A的延伸，用于还原A的变换。
求解A-1除了之前的初等变换方法外，我们还可以通过代数余子式的方式求解。
余子式：在一个n阶行列式D中,把元素aij (i,j=1,2,…..n)所在的行与列划去后，剩下的(n-1)^2个元素按照原来的次序组成的一个n-1阶行列式Mij,称为元素aij的余子式。
代数余子式：余子式Mij带上符号(-1)^(i+j)称为aij的代数余子式,记作Aij=(-1)^(i+j) Mij。
余子式相当于某一面的片面维度积，我们按正负将他们运算组合就可以得到实际维度积。
两种计算过程中需要的矩阵。
伴随矩阵：A*,每项为矩阵的代数余子式。伴随矩阵用来求逆：A-1=A*/|A|。
增广矩阵：将线性方程组的前后两个部分写在一个矩阵中，通过化简求解或者通过秩来判断解的个数。这就引入了一个工具秩。
秩：矩阵A的列秩是A的线性独立的纵列的极大数。通常表示为r(A)，rk(A)或rank A。
相似矩阵：相似矩阵是通过一个变换在不同视角的表现形式，它们的特点相同。我们可以通过计算相似矩阵来简化运算。B=P-1AP,该公式可以简单理解为矩阵B与后面三个矩阵的组合效果相同。假设我们有一个向量x，让x进行B变化，等到在B所在视角下的变换结果。等号右面让x先做P变换，将坐标点变换到A所在的坐标系当中，然后对变换点做A变换，然后将变换结果逆变换到B的坐标系下。这时我们发现两个结果相同，显然很容易理解这个结果。
第四节：特征值，特征向量与二次型
特征值和特征向量在机器学习等的算法中极为常见也十分重要，这里对他们实际表示的意义和特点做一个简单的理解。
设T是数域K上的线性空间Vn的线性变换，且对K中某一数a，存在非0向量x属于Vn，使得Tx=ax成立，则称a为T特征值，x为T的属于a的特征向量。
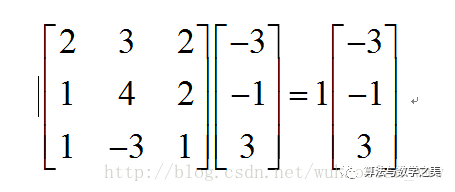
如上式：1为矩阵的特征值，向量为特征向量。那么他们分别代表什么含义呢。我们知道，矩阵乘法对应了一个变换，是把任意一个向量变成另一个方向或长度都大多不同的新向量。在这个变换的过程中，原向量主要发生旋转、伸缩的变化。如果矩阵对某一个向量或某些向量只发生伸缩变换，不对这些向量产生旋转的效果，那么这些向量就称为这个矩阵的特征向量，伸缩的比例就是特征值。根据之前提到缩放因子，我们知道这个矩阵可以变换成对角阵。但是它对机器学习中的特征提取有什么用呢？首先声明机器学习中的特征值并不是矩阵论中的特征值，机器学习中的特征值是指变化较为显著，能作为描述一个物体的一个主要特点。当我们有一百个方面来描述一个物体时，我们发现它的计算量十分庞大而且有些方面对结果几乎不起作用，这时候我们就需要提取出它的主要特征。目的是让所有样本尽量分散，这样数据信息就能更充分的表现出来，我们就很容易通过简单的曲线将数据分类。为了将数据分散，我们先列出所有方面的两两协方差矩阵。实对称矩阵可以化成对角矩阵，而且两个矩阵相似，通过对角矩阵我们不难发现，经过变换后某些维度的数据信息较为分散，即对角阵上较大的特征值，我们将这几个特征值选取出来，并提取他们的特征向量，该向量描述了一种变换，我们将这些方向的变换向量组成一个变换矩阵，然后将原始数据变换到新的空间。该空间的数据就会相对分散，易于分类。
详细解释见博客：
http://www.360doc.com/content/13/1124/02/9482_331688889.shtml
二次型：n个变量的二次多项式称为二次型，即在一个多项式中，未知数的个数为任意多个，但每一项的次数都为2的多项式。这个概念和我的学习内容不太相关就没有仔细看，提一下以后用到再回头学习。
到此终于结束。仅仅记录一下自己初看矩阵论的想法，肯定是漏洞百出，以后再看肯定会有不同的感悟和见解，以后的感悟以后再做记录。上面只是将抽象的东西讲的便于理解，并没有严谨的证明。所以认真推导和练习是必不可少的。
— 完 —
交流群
欢迎加入公众号读者群一起和同行交流，目前有SLAM、三维视觉、传感器、自动驾驶、计算摄影、检测、分割、识别、医学影像、GAN、算法竞赛等微信群（以后会逐渐细分），请扫描下面微信号加群，备注：”昵称+学校/公司+研究方向“，例如：”张三 + 上海交大 + 视觉SLAM“。请按照格式备注，否则不予通过。添加成功后会根据研究方向邀请进入相关微信群。请勿在群内发送广告，否则会请出群，谢谢理解~