什么是张量？你躺平一下就知道了。-技术圈

学习里经常出现张量（Tensor），这个概念说平常也很平常，但它背后涉及的数学并不算浅显。

张量这个词在不同领域的人看来貌似有点一词多意。一般来说，你只要知道张量是一个多维数组，差不多也就够了。比如著名的 Tensorflow 里的这个 tensor。

但如果真要掌握和应用相关的数学理论，那非得了解更多不可。1

张量小史

先来一碟开胃菜，大概了解下这个词以及相关理论的发展历程。

这里主要罗列相关概念的提出者及年代，而它们之间的传承关系由于缺乏引文不一定可考。历史真相的来龙去脉有时候只能凭大家遐想了。

1、先看张量积这个概念。大概 1884 年左右，美国物理学家 Gibbs（吉布斯）引入了中向量的张量积这个概念（他当时命名为 indeterminante product），后来他将其推广到维。

Gibbs 这样命名的原因是他认为这个乘积是两个向量乘积的最一般形式，它只需要满足作为积（product）的基本定律，即所谓的双线性，而不需要考虑其他任何定律，也因此具有很大不确定性。个人感觉 Gibbs 这点为张量的现代版数学定义奠定了基础。

2、德国物理学家 Voigt（福格特）于 1898 年使用张量来描述晶体上的应力和应变，这就是具有现代意义的张量这个词的首次出现。

3、意大利数学家 Ricci（里奇）在 1880-1890 年间将张量应用于微分几何，整出了所谓的绝对微积分。随后，Ricci 与学生 Levi-Civita (列维-奇维塔) 共同构建了张量分析，为爱因斯坦的广义相对论奠定了理论基础。张量一词在物理学和数学中得到广泛使用可能部分归功于爱因斯坦。

4、至此，张量积是由向量空间构建的。二十世纪，有人将张量积扩展到模（module）。

说了这么多，也没有看到张量到底是个什么东西？是吧，说明这个词不是一两句话就能解释清楚了。但这里大家可以看到，张量似乎离不开张量积。

张量的定义

我们来看看现代版的定义，翻一下数学书，或者看下 wikipedia，发现是下面这样子的。

Given a finite set of vector spaces over a common field one may form their tensor product an element of which is termed a tensor. A tensor on the vector space is then defined to be an element of (i.e., a vector in) a vector space of the form:

V \otimes \cdots \otimes V \otimes V^{\star} \otimes \cdots \otimes V^{\star}

where is the dual space of .

If there are copies of and copies of in our product, the tensor is said to be of type and contravariant of order and covariant order and total order . The tensors of order zero are just the scalars (elements of the field , those of contravariant order 1 are the vectors in and those of covariant order 1 are the one-forms in (for this reason the last two spaces are often called the contravariant and covariant vectors). The space of all tensors of type is denoted

T_{n}^{m}(V)=\underbrace{V \otimes \cdots \otimes V}_{m} \otimes \underbrace{V^{\star} \otimes \cdots \otimes V^{\star}}_{n}.

这里光定义，就有线性（向量）空间、张量积、对偶空间、协变、逆变等概念，初次看到的同学可能一头雾水。

我们再来看一个形式上更简练一点的，

定义设为向量空间的对偶空间，称重线性函数，

\mathcal{F}: \overbrace{V^{\star} \times \cdots \times V^{\star}}^{m 个} \times \overbrace{V \times \cdots \times V}^{n 个} \rightarrow R

为向量空间上的型张量（tensor)。

并将向量空间上的所有型张量构成的集合记为:

L(\overbrace{V^{\star}, \cdots, V^{\star}}^{m 个}, \overbrace{V, \cdots, V}^{n 个} ; R)

原来在数学家眼里，张量就是一个多重（chong，二声）线性函数啊。

那么，这个函数的输入输出分别是什么呢？看定义，输入是对偶空间里的个向量以及向量空间里的个向量，而输出就是一个实数，这里的个数可以是 0。

这样说貌似比较数学，工科同学或许得去补一些功课。咱先别管对偶空间啥的，今天我们想通过一个比较简单的例子来阐述一下张量这个概念。

下面正式开始我们的故事。3

躺平也能搞事情

在试图理解张量之前，我们先了解一下两个概念，即逆变和协变。它们描述了几何上或物理中的某些量是如何随着基的改变而规律地改变的。

等等，这些跟躺平有啥关系呢？看了半天没看到实质内容啊，太标题党了吧。

表急，我们来看一个式子，

[u, v] \begin{bmatrix} x \\ y \end{bmatrix} = ux + vy

上面四个数都来自实数域。

这时，有个叫小明的同学举手了，问：老师，这不是两个向量搞内卷吗？哦不，搞内积吗？

老师：可以这么看。但是注意，这里我们并不把这个运算当作向量的内积，而是两个来自不同星星（空间）的同学（向量）一起搞事情。

为了形象一些，你也可以把上式看成一个行向量和一个列向量作了某种运算。总之，它俩一结合，变出来一个实数。

注意看，它们中一个是躺着的，一个是站着的，姿势是不同的。

其实它们对应着不同的张量。那么到底怎么个不同呢？

我们来打个比方，假设它们对应两类青年，一类躺平青年，一类上进青年。（躺平的反面是上进吗？我不知道，这里咱们姑且这么说吧）。

但是这里想说的是，躺平并不代表不干活，甚至不能说不上进，而仅仅是干活的姿态不同而已。

言归正传，上面两个不同张量怎么干活呢？这里所谓的干活就是给它输入某些东西，它出来另外一些东西。用数学概念来说就是一个映射，因为这里最后出来的是一个数，所以是一个函数。

先看躺平向量对应的那个张量的干活姿势。我们将这个躺平向量记为，给它输入一个上进向量，它们俩深入沟通一番，融为一体，出来一个数。对，就是下面这样子，

[a, b] \begin{bmatrix} x \\ y \end{bmatrix} = ax + by

不妨改写一下，变成函数的样子，

\mathcal{F}_{[a,b]}\left(\begin{bmatrix} x \\ y \end{bmatrix}\right) = ax + by

这就是给定的某个躺平向量的干活姿势。因为这里是指定的某个躺平向量，所以上面的和是固定的，而和是可变的。给定一个躺平向量，它出的活（生的娃）可能差别挺大，就看你给它配的是怎么样的上进向量了。

再啰嗦一下，假设这里的躺平向量是你自己，那么给你配个上进向量（对象），你俩就能出活啊。给你不同的对象，你能出不同活。给你个女神男神，你出的活好。。。总之，你躺在那里，等着对象来，无限可能。

好了，该醒过来了。再次看一下上面这个函数，发现它还是个线性函数，即满足

\begin{array}[ccc]{} \mathcal{F}_{[a,b]}\left(\lambda_1 \begin{bmatrix} x_1 \\ y_1 \end{bmatrix} + \lambda_2 \begin{bmatrix} x_2 \\ y_2 \end{bmatrix}\right) = \lambda_1 \mathcal{F}_{[a,b]}\left(\begin{bmatrix} x_1 \\ y_1 \end{bmatrix} \right) + \lambda_2 \mathcal{F}_{[a,b]}\left(\begin{bmatrix} x_2 \\ y_2 \end{bmatrix}\right) \end{array}

不过，这里还忽略一个事情，那就是你这个躺平向量的和以及上进向量里的和都是些啥东西啊？对应出生吗？或者天赋、内在属性什么的？我们先不管它们代表什么，只考虑这个形式。

芸芸众生，皆是蝼蚁。

蝼蚁是不是很小啊。对，小到可以忽略大小，就是数学中的点，坐标点。

既然是坐标点，那就得涉及坐标系了。

我们先来看上进向量的坐标，它是根据世界坐标系（这里是二维的）而言的，即隐藏着一组基。下面，把它们写出来看看，

{\bf s} = \begin{bmatrix} \color{red}{1} & \color{blue}{0} \\ \color{red}{0} & \color{blue}{1} \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} = [\color{red}{e_1}, \; \color{blue}{e_2}]\begin{bmatrix} x \\ y \end{bmatrix} = x{e_1} + y {e_2}

换句话说，点的坐标对应着背后的坐标轴（基向量）。

小明同学提问：那么当基变了以后，点的坐标是不是也得变呢？

是的，问题是怎么变呢？好，下面咱们就来摸索下这个规律。

已知一个线性空间的两组基和（统一看成列向量），我们可以用一个矩阵来表示它们之间的转换关系，

[e_{1^{\prime}},e_{2^{\prime}},\cdots , e_{n^{\prime}}]= \left[e_{1},e_{2},\cdots,e_{n}\right] \left[\begin{array}{cccc} a_{1^{\prime}}^{1} & a_{2^{\prime}}^{1} & \cdots & a_{n^{\prime}}^{1} \\ a_{1^{\prime}}^{2} & a_{2^{\prime}}^{2} & \cdots & a_{n^{\prime}}^{2} \\ \vdots & \vdots & \ddots & \vdots \\ a_{1^{\prime}}^{n} & a_{2^{\prime}}^{n} & \cdots & a_{n^{\prime}}^{n} \end{array}\right]= \left[e_{1},e_{2},\cdots,e_{n}\right]\boldsymbol{A}

上式可以看成矩阵乘法。如果把基向量单独拿出来看，就是。

对于中向量，有，而其在另一组基下的表示为

u=\sum_{i^{\prime}}u^{i^{\prime}} e_{i^{\prime}}=\sum_{i^{\prime}}u^{i^\prime} \sum_{i} a^{i}_{i^{\prime}}e_{i}=\sum_{i}\color{red}{ \sum_{i^{\prime}}u^{i^\prime} a^{i}_{i^{\prime}}}e_{i}

对比红色部分，得。将其写成矩阵形式:

\left[\begin{array}{c} u^{1} \\ u^{2} \\ \vdots \\ u^{n} \end{array}\right]= \left[\begin{array}{cccc} a_{1^{\prime}}^{1} & a_{2^{\prime}}^{1} & \cdots & a_{n^{\prime}}^{1} \\ a_{1^{\prime}}^{2} & a_{2^{\prime}}^{2} & \cdots & a_{n^{\prime}}^{2} \\ \vdots & \vdots & \ddots & \vdots \\ a_{1^{\prime}}^{n} & a_{2^{\prime}}^{n} & \cdots & a_{n^{\prime}}^{n} \end{array}\right] \left[\begin{array}{c} u^{1^{\prime}} \\ u^{2^{\prime}} \\ \vdots \\ u^{n^{\prime}} \end{array}\right]=\boldsymbol{A}\left[\begin{array}{c} u^{1^{\prime}} \\ u^{2^{\prime}} \\ \vdots \\ u^{n^{\prime}} \end{array}\right]

由此可得:

\left[\begin{array}{c} u^{1^{\prime}} \\ u^{2^{\prime}} \\ \vdots \\ u^{n^{\prime}} \end{array}\right]=\boldsymbol{A}^{-1}\left[\begin{array}{c} u^{1} \\ u^{2} \\ \vdots \\ u^{n} \end{array}\right] \qquad (1)

回到我们二维的例子，上进向量的老坐标为。那么，在新的坐标系下坐标会变成什么呢？代入上面式（1），假设这里基变换矩阵仍然用表示，则有

\left[\begin{array}{c} x^{\prime} \\ y^{\prime} \end{array}\right]=\boldsymbol{A}^{-1}\left[\begin{array}{c} x \\ y \end{array}\right]

为了加深印象，我们来看个图。

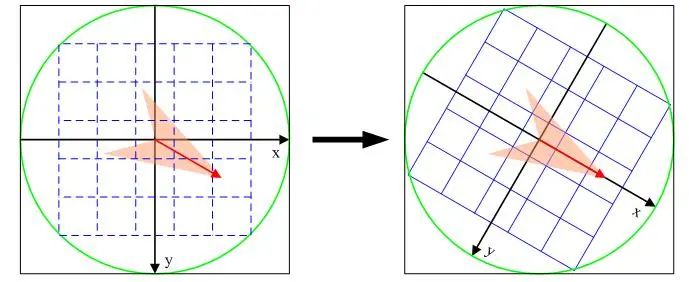
这里假设坐标系之间的变换是旋转，右图表示将原坐标系顺时针旋转 30 度。此时，红色那个向量还是原来的向量，大小和方向都没变，但它的坐标变了。坐标是不是变为逆时针旋转 30 度？顺时、逆时相同度数，它们对应的矩阵刚好互逆。

还记得你要和它一起搞事情吗？对，就是下面这个

[a, b] \begin{bmatrix} x \\ y \end{bmatrix} = ax + by

但这个时候你和它的坐标都已经变了，要用新的基来表示。具体就是下面这个样子了，

[a^{\prime}, b^{\prime}] \begin{bmatrix} x^{\prime} \\ y^{\prime} \end{bmatrix} = a^{\prime}x^{\prime} + b^{\prime}y^{\prime}

代入的旧坐标，得

[a^{\prime}, b^{\prime}] \begin{bmatrix} x^{\prime} \\ y^{\prime} \end{bmatrix} = [a^{\prime}, b^{\prime}] \;\boldsymbol{A}^{-1}\left[\begin{array}{c} x \\ y \end{array}\right]

还记得你们搞出来的数吗，就是。观察一下，如何让你的新坐标代入上式得到相同的结果呢？其实很方便，为了让你能够与任意上进向量保持搞相同事情的能力，你的坐标可以变换成下面这个样子，

[a^{\prime}, b^{\prime}] = [a, b]\;\boldsymbol{A}

这样就有，

\begin{array}[ccc]{} [a^{\prime}, b^{\prime}] \begin{bmatrix} x^{\prime} \\ y^{\prime} \end{bmatrix} &= [a^{\prime}, b^{\prime}] \;\boldsymbol{A}^{-1}\left[\begin{array}{c} x \\ y \end{array}\right] \\[1em] &= [a, b]\;\boldsymbol{A} \;\boldsymbol{A}^{-1}\left[\begin{array}{c} x \\ y \end{array}\right] \\[1em] &=ax + by \end{array}

上面中间两矩阵相乘很自然就消掉了。

☐逆变与协变

上面这个过程说明啥？

我们来画龙点睛一下，上进向量的坐标是这样变的，

\left[\begin{array}{c} x^{\prime} \\ y^{\prime} \end{array}\right]=\boldsymbol{A}^{-1}\left[\begin{array}{c} x \\ y \end{array}\right]

有个矩阵求逆是吧，所以叫逆变。

而你躺平向量是这样变的，

[a^{\prime}, b^{\prime}] = [a, b]\;\boldsymbol{A}

直接用了基的变换矩阵，不需要求逆矩阵。换句话说就是跟基一样的变化，所以叫协变。

所以，大家明白了吗？所谓上进向量，得逆势而上，自然是要有顽强的拼搏精神。而躺平向量比较佛系，顺势而躺即可。

逆势而上，顺势而躺。

需要注意的是，躺平向量和上进向量其实是在不同的空间里的。上进向量所在的空间就是我们一般指的向量空间，而躺平向量是在这个向量空间的对偶空间里。你也可以把它叫做对象空间，即你对象所在的空间。

你，作为躺平向量，和某个上进向量搞出某个小孩，是你本身固有的能力，是不会因为向量空间用的基不同而改变的。就是说，你和某个指定的上进向量的坐标在基改变后也都改了，但是你俩出来的娃（函数值）是不变的。

☐小结一下

张量，从数学上看就是一个多重线性函数，应用到几何上就对应一个几何量，应用到物体上就对应一个物理量。这些张量吃进若干个上进向量和躺平向量，吐出一个实数，吃进去的向量是会随着向量空间的基改变而改变，或逆变或协变，而这些吐出的数并不会随着基的改变而改变。从形式上看，这些张量在给定的基下面对应一个具体的多维数组，这个数组也会随着基的改变而规律地改变。

上面的例子中，你这个躺平向量与任意上进向量搞事情的这个线性函数就是一个张量。注意，这个函数的输入是一个上进向量，即吃进一个上进向量，吐出一个实数。而这一切都是你这个躺平向量决定的。这里的张量，不是指你这个躺平向量，而是指你和上进向量搞某个事情的本领。这个本领就是一个线性函数，即

\mathcal{F}_{你}(上进向量 X) = 你和上进向量捣鼓出来的一个实数

而且这个本领不会随着基（坐标系）的改变而改变。但是你和那些上进向量是会随着基的改变而改变的，只是改变的方式不一样。而你和它们搞事情的本领（张量）是不会随着第三者视角不同而不同的，可以认为是一种客观存在。

总之，给定一个躺平向量，就能像上面那样定义一个张量。那么小明同学可能又要问了，给定一个上进向量呢？能不能也定义一个张量呢？

还真可以，还是上面那个搞事情法子。给定一个上进向量，它可以和很多躺平向量搞事情啊。比如，还是搞刚才那个事情，

[u, v] \begin{bmatrix} c \\ d \end{bmatrix} = uc + vd

改成函数形式，

\mathcal{F}_{\begin{bmatrix} c \\ d \end{bmatrix}}\left([u, v]\right) = uc + vd

只不过，这个时候，上进向量是固定的，躺平向量是任意的。

其实，我们这里讲的这个搞事情的法子就对应了两个张量，一个是型张量，一个是型张量。这个时候，你应该拉到上面再来重新看一下型张量的定义。

☐灵魂之问

最后来回答一个灵魂之问：为什么要躺平？

从上面的例子来看，躺平不就是为了和上进青年一起搞事情嘛。对，躺下来就是为了睡上进青年。

你上进，我躺平，此消彼长，活不变。

是不是多少有几分，

躲进小楼成一统，管他冬夏与春秋。4

小明又举手了

这时，小明的同学又举手了，问：老师，如果两个上进向量或两个躺平向量，能一起搞事情（张量）吗？

老师：这不就是搞基嘛，也不是不行啊，只不过跟上面的例子不同，要其他搞法啦。

怎么搞基，还有上文中的对偶空间具体怎么肥事，我们下回再聊。