AutoML入侵强化学习!Google用「元学习」来强化学习,ICLR2021已接收

新智元报道
新智元报道
来源:google
编辑:LRS
【新智元导读】元学习是一种让机器去学习如何灵活学习解决问题的一种技术。谷歌的新工作使用符号图来表示并应用AutoML的优化技术来学习新的、可解释和可推广的强化学习算法。目前已被ICLR 2021接收。
近年来,AutoML在自动化机器学习的设计方面已经取得了巨大的成功,例如设计神经网络体系结构和模型更新规则。
神经架构搜索(NAS)是其中一个重要的研究方向,可以用来搜索更好的神经网络架构以用于图像分类等任务,并且可以帮助设计人员在硬件设计上找到速度更快、能耗更低的架构方案。
除NAS之外,谷歌之前的研究AutoML-Zero甚至还可以从零开始使用基本数学运算设计一个完整的算法。
但这些方法是为监督学习而设计的,总体算法更加简单明了,拿到标签,然后训练。
但对于强化学习来说,目标可能没有那么明确,例如采样策略的设计、整体的损失函数等,模型的更新过程并不是很明确,组件搜索的空间也更大。
自动化清华学习算法之前的工作主要集中在模型更新规则上。这些方法学习更好的优化器、更新本身的策略,通常用神经网络(RNN或CNN)表示更新规则,使用基于梯度的方法进行优化。
但是,这些学习的规则无法解释,也不具有泛化性,因为模型权重的获得过程是不透明的,并且数据也是来源于特定领域的。
强化学习算法和计算图
强化学习算法和计算图
NAS在神经网络体系结构的图的空间中进行搜索,受NAS的想法启发,本文通过将RL算法的损失函数表示为计算图来元学习强化学习算法。
在这种情况下,将有向无环图用于损失函数,节点代表输入、运算符、参数和输出,将增强AutoML的可解释性。
例如,在DQN的计算图中,输入节点包括来自缓冲区的数据,运算符节点包括神经网络运算符和基本数学运算符,而输出节点表示损失,通过梯度下降法来优化模型。
这种表示有一些好处,既能表示现有的算法,也可以定义新的未被发现的算法,并且也是可解释的。
如果研究人员可以理解为什么学习的算法更好,那么他们既可以修改算法的内部组成部分来改进它,又可以将有益的组成部分转移到其他问题上。
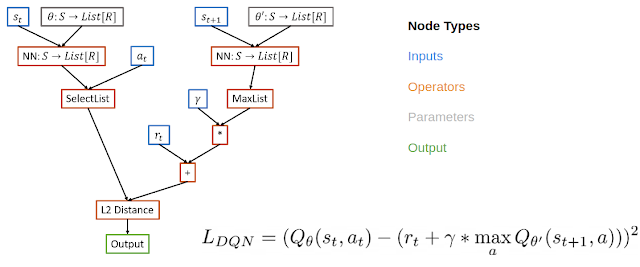
这种表示形式很容易通过PyGlove库实现,它可以将图形方便地转换为正则化优化的搜索空间。
会进化的RL算法
本文提出的强化学习算法是基于进化的方式。
首先,我们用随机图初始化一群训练的agent,在一组训练环境中并行训练。agent首先在类似CartPole这样的简单环境上进行训练,目的是快速清除性能不佳的程序。如果agent无法解决简单环境,就会以0分的分数提前停止,否则训练将会进入更难的环境,例如Lunar Lander等,评估算法的性能并将其用于更新整体的权重,在这些训练器中,更有前途的算法会进一步发生变异。
为了减少搜索空间,论文中使用功能等效检查器,如果它们在功能上与先前检查过的算法相同,则会跳过实验直到提出新的算法。
随着新的变异候选算法的训练和评估,该循环继续进行。在训练结束时,我们选择最佳算法并在一系列看不见的测试环境中评估其性能。
实验中的数据规模大概是300个训练器,我们观察到205000个突变后良好的候选进化,需要大约三天的训练时间。我们之所以能够在CPU上进行培训,是因为训练环境非常简单,可以控制训练的计算和能源成本。为了进一步控制训练成本,我们使用人工设计的RL算法(例如DQN)为初始种群播种。
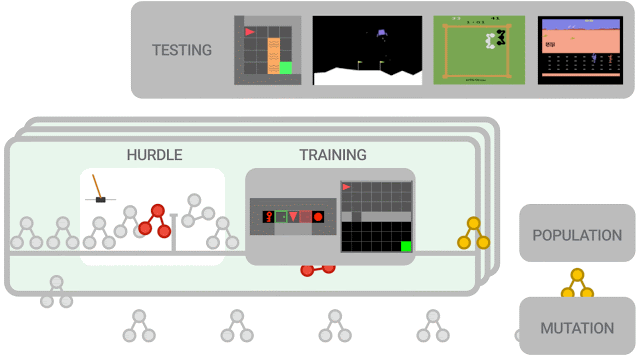
我们重点介绍两种发现的算法,它们表现出良好的泛化性能。第一个是DQNReg,它基于DQN,在Q值上额外增加正则平方的Bellman误差。第二个学习的损失函数DQNClipped,Q值的最大值和Bellman误差平方(以常数为模)。两种算法都可以看作是归一化Q值的一种。虽然DQNReg添加了软约束,但DQNClipped可以解释为一种约束优化,如果Q值太大,它将最小化Q值。在训练的早期阶段,高估Q值是一个潜在的问题时,一旦满足此约束条件,损失函数将最小化原始的平方Bellman误差。
尽管DQN等基准通常高估了Q值,但我们学到的算法以不同的方式解决了这一问题。DQNReg低估了Q值,而DQNClipped具有与double dqn类似的行为,因为它会缓慢地接近真实值。
值得指出的是,当使用DQN进行演化时,这两种算法会不断迭代出现。
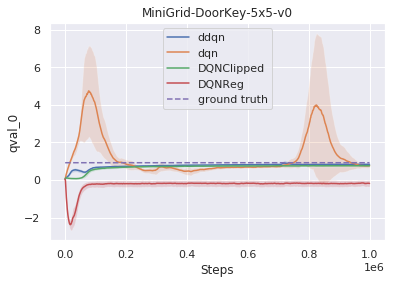
通常在RL中,泛化是指经过训练的策略,可以跨任务进行泛化。在一组经典控制环境上,学习到的算法可以匹配密集奖励任务(CartPole,Acrobot,LunarLander)上的基线,而在稀疏奖励任务MountainCar上优于DQN 。
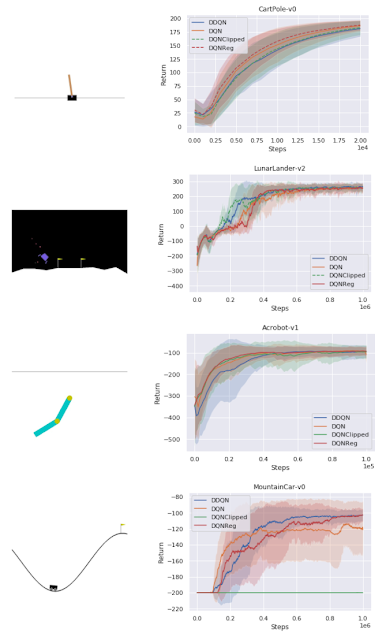
在测试各种不同任务的一组稀疏奖励MiniGrid环境中,我们发现DQNReg在样本效率和最终性能方面都大大优于训练和测试环境的基线。实际上,在尺寸、配置和熔岩等新障碍物存在变化的测试环境中,效果甚至更为明显。
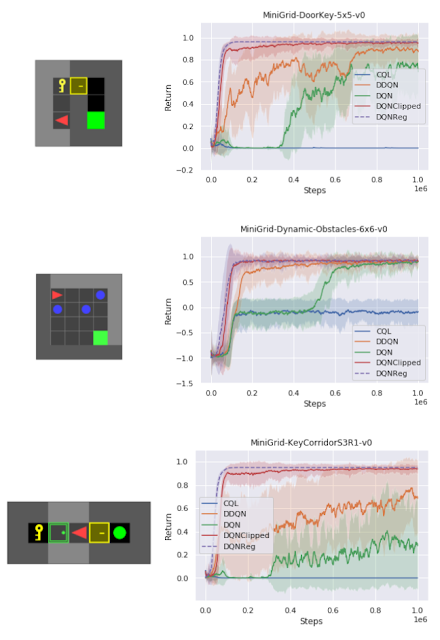
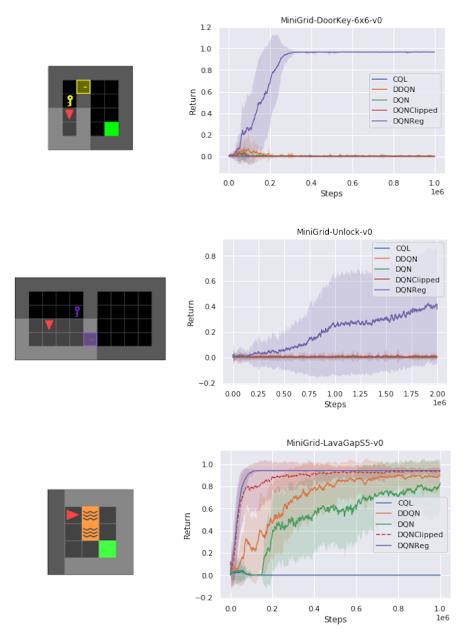
这些环境的起始位置,墙面配置和对象配置在每次重置时都是随机的,这需要agent进行概括而不是简单地记住环境,尽管DDQN经常努力学习任何有意义的行为,但DQNReg可以更有效地学习最佳行为。

无论是在非图像的环境上进行训练,还是在基于图像的Atari环境上,这种表示方法都能带来性能上的提升。这表明,这种元学习算法的通用性。
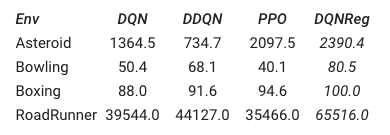
这篇论文讨论了如何将新的强化学习算法的损失函数表示为计算图,并在此表示形式上扩展多个agent训练来学习新的可解释RL算法。
计算图使研究人员既可以建立在人为设计的算法上,又可以使用与现有算法相同的数学工具集来学习算法。这些算法的性能超过之前的baseline系统,并且可以用于非视觉类的任务。
文章的作者希望这项工作可以促进机器辅助算法的开发,未来计算元学习可以帮助研究人员找到新的研究方向。
参考资料:
https://ai.googleblog.com/2021/04/evolving-reinforcement-learning.html
推荐阅读:

AI家,新天地。西山新绿,新智元在等你!
【新智元高薪诚聘】主笔、高级编辑、商务总监、运营经理、实习生等岗位,欢迎投递简历至wangxin@aiera.com.cn (或微信: 13520015375)
办公地址:北京海淀中关村软件园3号楼1100

