想理解深度学习,究竟应该降维打击 or 升维思考?
↑↑↑点击上方蓝字,回复资料,10个G的惊喜
B. 神经网络是一种计算图,多维数组流经其中。
C. 神经网络由层组成,每层都具有「神经元」。
D. 神经网络是一种通用函数逼近器。

正确答案是……ABCD。

前Facebook数据科学家塞思·韦德曼
图源:sethweidman.com
在其著作《Python深度学习入门:从零构建CNN和RNN》中,韦德曼写道:
对于讲解神经网络,我发现最具挑战性的就是为「什么是神经网络」传达正确的思维模型。这主要是因为,了解神经网络需要的不是一个而是多个思维模型,每一个都说明了神经网络工作方式的不同方面(而且每个方面都必不可少)。
诚然,神经网络与深度学习是一个立体的领域,仅从数学层面或代码层面学习,难免以偏概全,无法融会贯通。正因为如此,韦德曼提出了一种全新的学习方法:同时从数学、示意图、Python代码三个维度立体地理解每一个概念,从而领略深度学习领域的全貌。
想象你要构建自己的深度学习大厦。你或许钟情于算法,又或许习惯于视觉型学习,但唯有进行「升维思考」,你才能建造出多面玲珑的建筑。
韦德曼提出以如下步骤学习导数、嵌套函数、链式法则等概念。这些基本概念就如同一块块砖,有了它们,你终将建造出属于自己的深度学习大厦。
以一个或多个方程式展示数学原理。 给出示意图,类似于在参加编码面试时画在白板上的图。 给出对应的Python代码。
让我们一起看看用这种学习方法如何理解导数的概念。
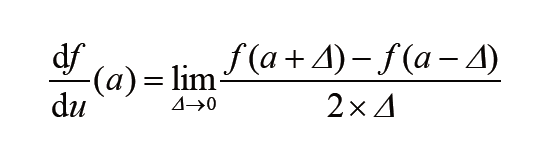
通过为Δ设置非常小的值(例如0.001),可以在数值上近似此极限。因此,如果Δ=0.001,就可以将导数计算为:
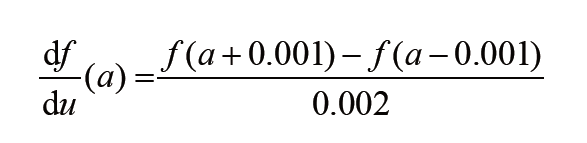
虽然近似准确,但这只是完整导数思维模型的一部分。下面来从示意图的维度认识导数。
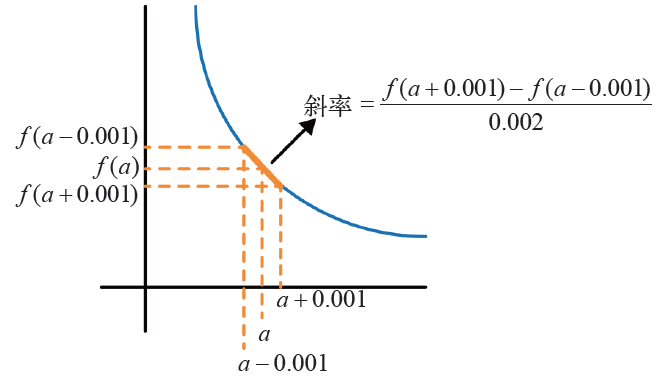
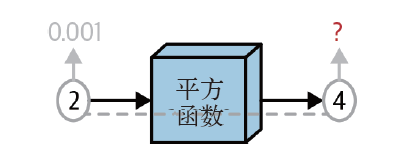
可以通过编码来求解前面看到的导数的近似值:
from typing import Callabledef deriv(func: Callable[[ndarray], ndarray],input_: ndarray,delta: float = 0.001) -> ndarray:'''计算函数func在input_数组中每个元素处的导数。'''return (func(input_ + delta) - func(input_ - delta)) / (2 * delta)
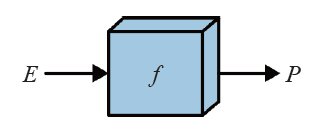
可以将其编码为下面这种形式。
def f(input_: ndarray) -> ndarray:# 一些转换return outputP = f(E)


郑天民 译
PyTorch神经网络实战
前Facebook数据科学家力作

也可以加一下老胡的微信 围观朋友圈~~~
推荐阅读
(点击标题可跳转阅读)
 点个「赞」
点个「赞」
求「在看」
评论
