面试官问我:什么是 “伸展树” ?

学过数据结构的小伙伴,一定都知道二叉查找树,也叫二叉排序树,英文缩写是BST。
为了维持二叉查找树的高效率查找,就需要对二叉查找树进行平衡调整。在数据结构当中大名鼎鼎的红黑树、AVL,就是典型的自平衡二叉查找树。
今天,我们来介绍一种更有意思的自平衡二叉树:伸展树。它的英文名字是Splay Tree。
Part 1 为什么要伸展
我们来回顾一下,二叉搜索树满足:
左子结点 < 当前结点 < 右子结点
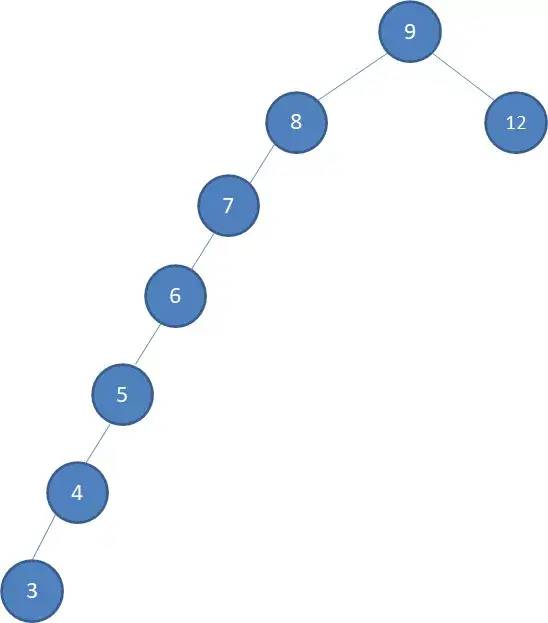
为什么要有平衡树呢?因为当二叉搜索树如下图“瘸腿”时,搜索左侧的结点,原来的速度 会掉到 ,与链表一个速度,失去了价值。为了避免树瘸腿,我们可以通过适当的旋转来调整树的结构。
伸展树的核心,是通过不断的将结点旋转到根结点(即为splay操作),来保证整棵树不会跟链表一样。它由 Daniel Sleator 和 Robert Tarjan 发明 。
1.1 结点
node中记录的信息:
parent:父结点的指针。child[0/1]:child[0]为左子结点的指针,child[1]为右子结点的指针。value:这个结点存了啥。count:二叉树中不存在两个值相同的结点,如果需要记录多个就需要一个变量来记录这个数值出现了多少次。(count就是来干这个活的)size:这个结点为根结点的子树中有多少个结点。
基础操作:
maintain:更新结点的size。(更新要自底向上)get:获取自己的类型,0为左子结点,1为右子结点。connect: 连接两个结点。
class node {
public:
node *parent; // 父结点的指针
node *child[2]; // child[0]为左子结点的指针,child[1]为右子结点的指针。
int value, count, size; // 数据,出现次数,子树大小
node(int _value) {
value = _value;
parent = child[0] = child[1] = NULL;
count = size = 1;
}
};
我们把对指针是否为NULL提到了两个基础操作中,所以只能放在伸展树的类中。
destroy:销毁整个树。因为结点使用的是堆空间(new出来的),所以必须要销毁(delete),否则会内存泄漏。
class splayTree {
public:
node *root;
splayTree() {
root = NULL;
}
~splayTree() {
destroy(root); // 从root开始销毁
}
void destroy(node *current) { // 销毁结点
if (current) {
destroy(current->child[0]); // 后序遍历
destroy(current->child[1]);
delete current;
}
}
void maintain(node *current) { // 更新size
if (current == NULL) { // 可能传入的是一个空指针
return;
}
current->size = current->count; // 先将自己加上
if (current->child[0]) { // 防止没儿子,NULL,报错
current->size += current->child[0]->size; // 加上儿子
}
if (current->child[1]) {
current->size += current->child[1]->size;
}
}
int get(node *current) { // 获得结点是左结点还是右结点,0左1右
if (current == NULL || current->parent == NULL) { // 传入空指针;根结点没有父亲,特判一下
return -1;
}
return current->parent->child[1] == current; // 父亲的右子结点 是不是 自己
}
void connect(node *parent, node *current, int type) { // 父结点指针,当前结点指针,类型(0左1右)
if (parent) { // parent 可能为NULL
parent->child[type] = current;
}
if (current) { // current 也可能为NULL
current->parent = parent;
}
}
};
可能会有读者好奇:这个size是用来干什么的呢?别急,等到查询排名时就会用到。
1.2 左旋 & 右旋
通过旋转,我们能在保证旋转可以保证左子结点 < 当前结点 < 右子结点的情况下调整结点之间的关系。
旋转有两种定义:
对以x为根的子树进行旋转。 把x向上旋转。
1.2.1 以x为根的子树进行旋转
1.2.2 把x向上旋转
上面的动画使用文字叙述即为:
左旋
将被旋转结点的左结点变为父结点的右结点。 父结点变为被旋转结点的左子结点 原父结点的父结点(爷爷)变为被旋转结点的父结点。 右旋
将被旋转结点的右结点变为父结点的左结点。 父结点变为被旋转结点的右子结点 原父结点的父结点(爷爷)变为被旋转结点的父结点。
虽然1、2两种旋转定义不同,但是只看移动这分明就是一种嘛。
有细心的读者发现:左右旋的方式与AVL、红黑树等其他二叉树相同。
因为这是唯一一种不改变中序遍历的旋转方式。
左旋与右旋都不会改变中序遍历的结果,如上方动图,中序遍历始终为1 y 2 x 3
除了举例论证,你也可以这样理解:
这是因为左旋和右旋会保证旋转后的二叉树
左子结点 < 当前结点 < 右子结点,因为旋转没有插入或删除结点,所以二叉树的中序遍历没变。
1.2.3 合并左右旋
想要合并左右旋,只能使用定义二:把x向上旋转。(原因见下)
左旋和右旋虽然属于两种操作,但是细想想:
一个结点不是左子结点,就是右子结点。因为我们要将结点向上旋转,所以每一个结点(除了根结点),只能朝一个方向旋转,也就是父结点的方向。
所以可以将两种操作整合为一种:
当被旋转的结点的类型为左子结点时,进行右旋。
当被旋转的结点的类型为右子结点时,进行左旋。
那么如何用一组代码来表达两种旋转呢?
我们之前对child定义为数组,那么可以使用child[数值]来决定访问的是左结点还是右结点。在内嵌套get(...),可以得到与被旋转结点类型相同的子结点。
如果get(...)得到的为0(左),怎样让其变成1(右),来访问右结点呢?
这个问题等同于将get(...)取反。
x ^ 1可以将0变1,1变0。!x,疑似可以,但get(...)的返回值为int型,不建议使用!。
下面这个动画对应左旋:
由于旋转改变了父子关系,所以当前结点与父结点的size会发生变化,需要重新更新。
旋转之后,父亲变为儿子,所以要先更新原父亲(被旋转结点在旋转前的父结点),后更新原儿子(被旋转结点)。
代码实现,注释中也藏了一些知识点(关于maintain的顺序):
void rotate(node *current) {
if (current == root || current == NULL) { // 根结点没有父结点,旋转不了;防止传入空指针后报错
return;
}
node *parent = current->parent; // 爹爹
node *grandParent = parent->parent; // 爷爷,可能是NULL
int type = get(current); // 被旋转结点的类型,0为右旋,1为左旋
int parentType = get(parent); // 爹爹的类型
connect(parent, current->child[type ^ 1], type); // 将三角形的结点挂到父结点
connect(current, parent, type ^ 1); // 儿子变父亲
if (parent == root) { // 如果父结点为根结点,需要将根结点指针更新
root = current;
}
connect(grandParent, current, parentType); // 爷爷认孙子为儿子
maintain(parent); // 此时parent(父亲)变为最底层的结点了,对其先进行更新
maintain(current); // parent结点更新之后,位于parent父亲位置的current进行更新
// 为啥不更新 grandParent 呢?是因为旋转是在 grandParent 以下的位置进行的,子树大小无变化。
}
下面的splay采用定义2,也就是上面的实现。
1.3 splay
splay名字很高大上,其实很简单。splay其实就是将某一个结点经过几次旋转后达到根结点位置。
当前结点、父结点与爷爷结点的位置不同,向上旋转的方式也不同。
前文,我们将左旋与右旋写到了一起,使用的定义是把x向上旋转,此时
splay的逻辑如下:
当前结点为x
如果x的父结点为根结点,直接对x进行旋转。 如果父结点不是根结点,且x与父结点的类型相同,对父结点进行旋转。 如果父结点不是根结点,且x与父结点的类型不同,对x进行旋转。
void splay(node *current) {
if (current == NULL || current->parent == NULL) { // 根结点没有父结点,会形成死循环;为current传入NULL以防万一
return;
}
while (current->parent->parent) { // 父结点不是根结点(是根结点的话get(current->parent)无法正常执行)
if (get(current) == get(current->parent)) { // 类型相同
rotate(current->parent);
} else {
rotate(current);
}
}
rotate(current); // 父亲为根结点,旋转自己篡位
}
1.4 查找
find(value)用于查找一个结点,其数据与value相同。
由于平衡树终究是在BST(二叉搜索树)之上进行变换,查找方式大体与BST相同:
如果 当前结点的值小于要搜索的值:向右结点查找(右结点比当前结点大)如果 当前结点的值大于要搜索的值:向左结点查找(左结点比当前结点小)如果两个值相等:恭喜你,找到结点了。 其中,如果在向子结点查找时,发现子结点为空,那么必然找不到结点了。(1、2都是对目标值进行逼近,不存在结点存在只是没有被搜索的情况)
可是伸展树有一个特性:在每执行完一次操作(查找、插入、删除等等)后都要对结点进行splay
在查找这种操作中,被查找的结点需要在查找到后进行splay
node* find(int value) {
node *current = root; // 从根结点开始搜索
while (current) {
if (current->value < value) {
current = current->child[1]; // 小了,往大了走
} else if (current ->value > value) {
current = current->child[0]; // 大了,往小了走
} else { // 不大也不小不就是找到了吗?
splay(current);
return current;
}
}
return NULL; // 找不到结点,退出。(找到得到结点的话会在while循环就退出)
}
1.5 查询排名
rank(value),值为value的结点的排名,为这个结点在中序遍历中排第几位。
虽然排名为中序遍历的排名,但是我们并不需要对整个树进行中序遍历。
排名可以看做:结点左面的结点个数 + 1(这个1对应它自己)由于我们事先不知道值
value对应哪一个结点,所以我们需要将上文的find整合进来。
维护一个变量leftSize,用于记录结点左侧共多少个结点,
如果当前结点的值大于要搜索的值:向左结点查找(左边没有结点, leftSize不改变)这个时候果断将 leftSize += 左子树大小,因为目标结点不是在当前结点就是在右结点,这两种情况都约过了左子树。
如果两个值相等,那么就是找到了,将leftSize += 1,对找到的结点进行splay,返回leftSize。(+ 1是自己的)2没有返回目标结点必然在右子树, leftSize += 当前结点的count向右结点查找吧。
int rankOfNode(int value) {
// 这里传入的value为被查询排名的结点的value
node *current = root; // 从根结点开始搜索
int leftSize = 0; // 左侧的所有结点总和
while (current) {
if (value < current->value) { // 目标结点小于当前结点,向左走
current = current->child[0];
} else {
// 无论是目标结点为当前结点,还是在右子树,都跨过了左子树
if (current->child[0]) { // 可能没有左子树
leftSize += current->child[0]->size;
}
if (value == current->value) {
leftSize += 1; // 加上自己的。你就想最左边结点leftSize = 0,可是排名是1
splay(current);
return leftSize;
}
// 找到结点的话会return,所以这里必然是目标结点大,向右走
leftSize += current->count; // 把当前结点越过,加上
current = current->child[1]; // 这个current变到右子结点是必须放在最后的,否则前面会乱
}
}
return -1; // 找不到结点,输出-1
}
1.6 查询排名为rank的结点
当我们知道了排名,怎样找对应的结点呢?
勘误:动画中判断应为
rank <= 0,而非rank == 0。由于例子中所有结点的count都为1,所以表面看来没有问题。
我们设 以当前结点为根结点的树中,需要查询排名为
rank。1.如果
rank > 左子树的size:
那么目标结点只能存在于当前结点与右子树之间。我们对 rank -= 左子树的size + 当前结点的count。
如果此时 rank <= 0,那么目标结点就在根结点。(一个极端例子,第一个结点的count为999,1 ~ 999都对应了这一个结点,rank -= count就会出现负数)如果此时 rank > 0,那么目标结点还在右结点,把当前结点设置为右结点,整个过程再来一遍。2.如果
rank <= 左子树的size:
那么目标结点肯定藏匿于左子树,将目标结点设置为左结点,再来一遍。 向右走,越过了左子树的所有结点与当前结点,所以要对
rank减越过的结点。
向左走,越过了空气什么也没有越过,故rank不动。
因为
rank在做完减法后就会判断是否为小于0,小于0就退出了。所以其余时间里rank > 0。
node* nodeOfRank(int rank) {
node *current = root; // 从根结点查找
while (current) {
if ((current->child[0] && rank > current->child[0]->size) || current->child[0] == NULL) {
// 1. 左子树存在,rank > 且左子树大小
// 2. 左子树不存在,大小可看做0。因为rank > 0,所以无需判断可知 rank > 左子树大小。
if (current->child[0]) {
rank -= current->child[0]->size;
}
rank -= current->count;
if (rank <= 0) {
splay(current);
return current;
}
current = current->child[1]; // 不是在左子树、当前结点,就是在右子树呗
} else {
current = current->child[0]; // 目标结点在左子树
}
}
return NULL;
}
1.7 前趋后继
前趋pre:比查询结点小的最大结点。
后继next:比查询结点大的最小结点。
由于结点的左子树任意一个结点都比当前结点小,在左子树中取最大的结点即为前趋。
后继同理,右子树任意一个结点都比当前结点大,在右子树中取最小的结点即为后继。
取最大值最小值与BST相同:
最大:找树的最右侧结点。(右 > 中 > 左)
最小:找树的最左侧结点。(左 < 中 < 右)
node* preNext(int type, node *current) { // 0为前趋,1为后继
if (current == NULL) {
return NULL;
}
splay(current);
current = current->child[type]; // 如果current没有左结点,那么current会变为NULL
while (current && current->child[type ^ 1]) { // current->child[1]用来避免current为NULL
current = current->child[type ^ 1];
}
splay(current);
return current;
}
1.8 插入
插入有三种情况:
整棵树是空的, root为NULL,这种情况下我们直接将结点放在root的位置即可。在树的已有结点中存在新插入的值,由于二叉搜索树中不能出现两个值一样的结点,所以对已有的结点的 count加1即可。树中没有这个新插入的值,那么我们需要找到合适的位置,在插入后进行 splay
第三种情况:
像 find的过程一样,当前结点小于插入值向右子树查找,当前结点大于插入值向左查找(等于就属于第二种情况了),直到当前结点为NULL,找到一个空位置。(这里我们需要记录当前结点的parent,因为NULL结点是记录不了信息的)连接 NULL位置的父结点 与 插入的结点。 splay插入结点。
node* insert(int value) {
if (root == NULL) {
root = new node(value);
return root;
}
node *current = root;
node *parent = current->parent;
int type; // 类型
while (current) { // 和查找一模一样
if (current->value < value) {
parent = current;
current = current->child[1];
type = 1;
} else if (current->value > value) {
parent = current;
current = current->child[0];
type = 0;
} else { // 已经有相同结点了,将其count++即可。
current->count ++;
splay(current);
return current;
}
}
current = new node(value);
connect(parent, current, type);
splay(current);
return current;
}
1.9 合并两棵树
合并两棵树,我们设它们的根结点分别为x和y。
要使两棵树能够合并,x中的最大值要小于y中的最小值。
合并过程:
x或y有一个树是空的,返回不是空的那个。x和y均不为空。splayx中的最大值。此时 x的根结点的右子树为空,将y作为x的右子树(因为右 > 中 > 左,x的最大值还在根结点,没有比最大值还有大的了,所有右侧没有结点)
合并操作需要在删除中遇到,动画与实现均在删除中。
1.10 删除
删除过程:
我们首先将被删除的结点进行 splay。销毁被删除结点,与左右子树断开联系。 合并两棵树(右合并到左)
// 求以current为根的树的最大与最小值
node* minMax(int type, node *current) { // type == 0为min,type == 1为max
while (current->child[type]) {
current = current->child[type];
}
splay(current);
return current;
}
void remove(node *current) {
splay(current);
if (current->count >= 2) {
current->count --;
return;
}
node *left = current->child[0];
node *right = current->child[1];
if (left) {
left->parent = NULL;
}
if (right) {
right->parent = NULL;
}
delete current;
if (left && right) { // 两个都有
left = minMax(1, left); // 求最大值最小值时默认进行了splay
right = minMax(0, right);
connect(left, right, 1);
root = left;
} else {
if (left) { // 只有左结点
root = left;
} else { // 只有右结点,或者两个都没有。两个都没有right为NULL,root就变成NULL了
root = right;
}
}
}
1.11 代码
LOJ上的普通平衡树[2]
我们上述的几种操作个个对应题目需要。但是当我们仔细读题:
求 的前趋(前趋定义为小于 ,且最大的数);
求 的后继(后继定义为大于 ,且最小的数)。
本文中的前趋后继为结点的前一个与后一个,而题目中 可能不存在,怎么办呢?
简单!将x插入到树中,进行查询,随后再删除不就行了吗?
完整代码如下,LOJ中不开优化测评记录[3]:
//
// Created by Cat-shao on 2021/5/8.
//
#include <cstdio>
#include <algorithm>
#include <deque>
using namespace std;
class splayTree {
public:
class node {
public:
node *parent; // 父结点的指针
node *child[2]; // child[0]为左子结点的指针,child[1]为右子结点的指针。
int value, count, size; // 数据,出现次数,子树大小
node(int _value) {
value = _value;
parent = child[0] = child[1] = NULL;
count = size = 1;
}
};
node *root;
splayTree() {
root = NULL;
}
~splayTree() {
destroy(root);
}
void destroy(node *current) {
if (current) {
destroy(current->child[0]);
destroy(current->child[1]);
delete current;
}
}
void maintain(node *current) { // 更新size
if (current == NULL) { // 可能传入的是一个空指针
return;
}
current->size = current->count; // 先将自己加上
if (current->child[0]) { // 防止没儿子,NULL,报错
current->size += current->child[0]->size; // 加上儿子
}
if (current->child[1]) {
current->size += current->child[1]->size;
}
}
int get(node *current) { // 获得结点是左结点还是右结点,0左1右
if (current == NULL || current->parent == NULL) { // 传入空指针;根结点没有父亲,特判一下
return -1;
}
return current->parent->child[1] == current; // 父亲的右子结点 是不是 自己
}
void connect(node *parent, node *current, int type) { // 父结点指针,当前结点指针,类型(0左1右)
if (parent) { // parent 可能为NULL
parent->child[type] = current;
}
if (current) { // current 也可能为NULL
current->parent = parent;
}
}
void rotate(node *current) {
if (current == root || current == NULL) { // 根结点没有父结点,旋转不了;防止传入空指针后报错
return;
}
node *parent = current->parent; // 爹爹
node *grandParent = parent->parent; // 爷爷,可能是NULL
int type = get(current); // 被旋转结点的类型,0为右旋,1为左旋
int parentType = get(parent); // 爹爹的类型
connect(parent, current->child[type ^ 1], type); // 将三角形的结点挂到父结点
connect(current, parent, type ^ 1); // 儿子变父亲
if (parent == root) { // 如果父结点为根结点,需要将根结点指针更新
root = current;
}
connect(grandParent, current, parentType); // 爷爷认孙子为儿子
maintain(parent); // 此时parent(父亲)变为最底层的结点了,对其先进行更新
maintain(current); // parent结点更新之后,位于parent父亲位置的current进行更新
// 为啥不更新 grandParent 呢?是因为旋转是在 grandParent 以下的位置进行的,子树大小无变化。
}
void splay(node *current) {
if (current == NULL || current->parent == NULL) { // 根结点没有父结点,会形成死循环;为current传入NULL以防万一
return;
}
while (current->parent->parent) { // 父结点不是根结点(是根结点的话get(current->parent)无法正常执行)
if (get(current) == get(current->parent)) { // 类型相同
rotate(current->parent);
} else {
rotate(current);
}
}
rotate(current); // 父亲为根结点,旋转自己篡位
}
node* find(int value) {
node *current = root; // 从根结点开始搜索
while (current) {
if (current->value < value) {
current = current->child[1]; // 小了,往大了走
} else if (current->value > value) {
current = current->child[0]; // 大了,往小了走
} else { // 不大也不小不就是找到了吗?
splay(current);
return current;
}
}
return NULL; // 找不到结点,退出。(找到得到结点的话会在while循环就退出)
}
int rankOfNode(int value) {
// 这里传入的value为被查询排名的结点的value
node *current = root; // 从根结点开始搜索
int leftSize = 0; // 左侧的所有结点总和
while (current) {
if (value < current->value) { // 目标结点小于当前结点,向左走
current = current->child[0];
} else {
// 无论是目标结点为当前结点,还是在右子树,都跨过了左子树
if (current->child[0]) { // 可能没有左子树
leftSize += current->child[0]->size;
}
if (value == current->value) {
leftSize += 1; // 加上自己的。你就想最左边结点leftSize = 0,可是排名是1
splay(current);
return leftSize;
}
// 找到结点的话会return,所以这里必然是目标结点大,向右走
leftSize += current->count; // 把当前结点越过,加上
current = current->child[1]; // 这个current变到右子结点是必须放在最后的,否则前面会乱
}
}
return -1; // 找不到结点,输出-1
}
node* nodeOfRank(int rank) {
node *current = root; // 从根结点查找
while (current) {
if ((current->child[0] && rank > current->child[0]->size) || current->child[0] == NULL) {
// 1. 左子树存在,rank > 且左子树大小
// 2. 左子树不存在,大小可看做0。因为rank > 0,所以无需判断可知 rank > 左子树大小。
if (current->child[0]) {
rank -= current->child[0]->size;
}
rank -= current->count;
if (rank <= 0) {
splay(current);
return current;
}
current = current->child[1]; // 不是在左子树、当前结点,就是在右子树呗
} else {
current = current->child[0]; // 目标结点在左子树
}
}
return NULL;
}
node* preNext(int type, node *current) { // 0为前趋,1为后继
if (current == NULL) {
return NULL;
}
splay(current);
current = current->child[type]; // 如果current没有左结点,那么current会变为NULL
while (current && current->child[type ^ 1]) { // current->child[1]用来避免current为NULL
current = current->child[type ^ 1];
}
splay(current);
return current;
}
node* insert(int value) {
if (root == NULL) {
root = new node(value);
return root;
}
node *current = root;
node *parent = current->parent;
int type; // 类型
while (current) { // 和查找一模一样
if (current->value < value) {
parent = current;
current = current->child[1];
type = 1;
} else if (current->value > value) {
parent = current;
current = current->child[0];
type = 0;
} else { // 已经有相同结点了,将其count++即可。
current->count ++;
splay(current);
return current;
}
}
current = new node(value);
connect(parent, current, type);
splay(current);
return current;
}
node* minMax(int type, node *current) { // type == 0为min,type == 1为max
while (current->child[type]) {
current = current->child[type];
}
splay(current);
return current;
}
void remove(node *current) {
splay(current);
if (current->count >= 2) {
current->count --;
return;
}
node *left = current->child[0];
node *right = current->child[1];
if (left) {
left->parent = NULL;
}
if (right) {
right->parent = NULL;
}
delete current;
if (left && right) { // 两个都有
left = minMax(1, left); // 求最大值最小值时默认进行了splay
right = minMax(0, right);
connect(left, right, 1);
root = left;
} else {
if (left) { // 只有左节点
root = left;
} else { // 只有右节点,或者两个都没有。两个都没有right为NULL,root就变成NULL了
root = right;
}
}
}
};
void LOJ104()
{
int n, opt, x;
splayTree tree = splayTree();
scanf("%d", &n);
for (int i = 1; i <= n; i++) {
scanf("%d%d", &opt, &x);
switch (opt) {
case 1: tree.insert(x); break;
case 2: tree.remove(tree.find(x)); break;
case 3: printf("%d\n", tree.rankOfNode(x)); break;
case 4: printf("%d\n", tree.nodeOfRank(x)->value); break;
case 5:
tree.insert(x);
printf("%d\n", tree.preNext(0, tree.find(x))->value);
tree.remove(tree.find(x));
break;
case 6:
tree.insert(x);
printf("%d\n", tree.preNext(1, tree.find(x))->value);
tree.remove(tree.find(x));
break;
}
}
}
int main()
{
LOJ104();
}
1.12 时间复杂度
伸展树可视化[4](需要将网址复制到浏览器中,网址见页脚)
在学完了伸展树的基础操作之后,我们发现主要是splay来维护整个二叉树平衡,然而splay后的树并不平衡。
伸展树的时间复杂度是均摊的 ,Tarjan是怎么将这个复杂度算出来的呢?
你百度一下,就会看见很多人使用了势函数来证明。
身为一个蒟蒻,我无法证明。可是,经过测试,伸展树与其他平衡树的速度大同小异。
1.13 与其他平衡树比较
| 红黑树 | AVL | fhq treap | splay(伸展树) |
|---|---|---|---|
| 速度最快 | 最平衡,查找最快 | 代码最好打 | ? |
这么看伸展树就一打酱油的,那这个东西到底有什么意义呢?
伸展树的优势在于操作多
欲知后事如何,且听下回分解!
参考与鸣谢
OI Wiki[5]:OIer的算法wiki,知识点全面但是小白看不懂,大家可以收藏。 KHIN[6]:问了KH很多问题,受益颇多。 manim幼儿园[7]:本文所有的动画皆为manim所做,manim幼儿园的视频教程十分详细。
伸展树算法偏难,你若有什么问题,欢迎回复,或者在LOJ的讨论[8]中发出你的观点。
讨论中可能会跟进一些内容(如前趋后继的更好实现、勘误)。
参考资料
splay tree demo: https://www.link.cs.cmu.edu/splay/
[2]LOJ上的普通平衡树: https://loj.ac/p/104
[3]LOJ中不开优化测评记录: https://loj.ac/s/1141137
[4]伸展树可视化: https://www.cs.usfca.edu/~galles/visualization/SplayTree.html
[5]OI Wiki: https://oi-wiki.org/ds/splay/#_11
[6]KHIN: https://www.luogu.com.cn/user/236807
[7]manim幼儿园: https://manim.wiki/
[8]LOJ的讨论: https://loj.ac/d/3181