说在前面
“走迷宫”是一个经典的算法问题:给定二维地图、入口和出口坐标,查找行走路径(或最短路径)。常见思路是使用深搜或广搜算法来寻找路径。
浙教版《信息技术选择性必修1数据与数据结构》5.2.2 递归中有一个“实践与体验”,项目名称是“走迷宫”,给定二维地图、入口和出口坐标,要求编程判断是否能从出口走出,即判断入口和出口是否连通。
相比输出路径,本题的难度降低了。教材程序采用简单的递归算法解决了该问题,思路清晰、代码简洁,对于巩固学生对递归算法的理解很有帮助。教师在教学中可以引导学生理解教材程序中各语句和变量的含义,分析程序输出两行“successful!”的原因,并思考如何对代码加以改进,如何使用非递归算法来解决此问题。
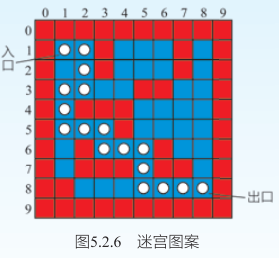
教材文本
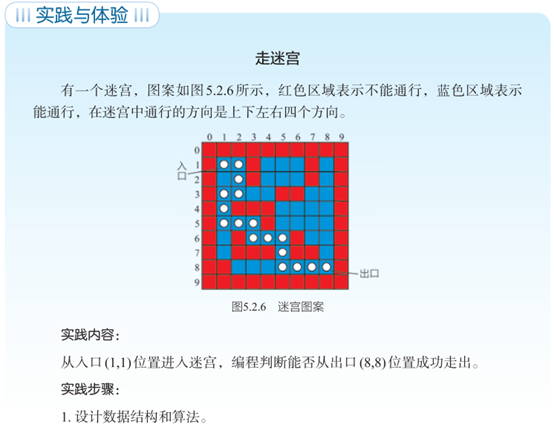



教材处理
教材给出了“走迷宫”案例的实践步骤,并提供了完整源代码和测试数据示意图。教师除了引导学生分析示意图,理解算法思想,还应该结合代码,帮助学生分析程序是如何实现算法思想的,是否有其他的算法设计和代码实现方式。
总体来说,书中程序算法逻辑清晰,代码简洁明了,值得学生认真体会。同时,教师可以趁热打铁,在例题的基础上做进一步拓展,引导学生分析例题代码的不足之处,思考改进方法,并回顾之前学习过的栈和队列,思考解决“走迷宫”问题的非递归算法。
学生任务单
阅读教材P125实践与体验“走迷宫”,思考如下问题:(1)书中程序使用二维数组maze存储迷宫图案,则len(maze)和len(maze[0])分别表示什么?(2)二维数组maze是用横轴坐标还是行列坐标来描述元素位置的?递归函数walk的形式参数x和y分别表示什么?(3)maze[x][y]表示什么?当其取值为0、1、2时分别有何含义?(4)递归函数walk的递归出口和递归体分别怎么表示? (5)运行书中程序后,输出了两行“successful!”,这是为什么?另外,当入口与出口不连通时,书中程序不会输出任何结果,你能否对程序加以改进,使其在找到出口时只输出一行“successful!”,并在找不到出口时,输出“failed!”。(6)如下程序能实现问题(5)的功能,试比较其与教材程序的异同,并做进一步简化。 return 0 <= r < len(maze) and 0 <= c < len(maze[0]) and maze[r][c] == 1 #依次向上左下右四个方向试探,若找到出口,则结束查找 return False # 未找到迷宫出口,返回False(7)计算机在执行递归程序时,是通过栈的调用来实现的。递归程序是将复杂问题分解为一系列简单的问题,从要解的问题起,逐步分解,并将每步分解得到的问题放入“栈”中,运用栈的“后进先出”的性质,这样栈顶是最后分解得到的最简单的问题,解决了这个问题后,次简单的问题可以得到答案,以此类推。所以,分解问题可以看作是进栈的过程,而解决问题则是出栈的过程。我们可以根据这个原理,通过构造一个栈,采用非递归算法来解决走迷宫问题,参考代码如下(仅对walk函数做了修改,其他代码不变),请将缺失的代码补充完整。
dirs = [[-1, 0],[0, -1],[1, 0],[0, 1]] st.append([r, c, 0]) #将起点坐标和初始朝向均入栈 for i in range(nextd, 4): #依次检查栈顶元素未探查方向 if nextr == 8 and nextc == 8: #若找到出口,则结束查找 maze[nextr][nextc] = 2 #做标记,防止折回 st.append([r, c, i+1]) #原位置和其下一方向入栈 st.append(填空4) #新位置和初始朝向入栈 break #退出内层循环,处理下一位置
return False
问题解析
(1)len(maze)表示总的行数,len(maze[0])表示总的列数。(2)二维数组maze是用行列坐标来描述元素位置的,参数x和y分别表示迷宫中某个位置的行、列坐标。将参数命名为x和y不太好,因为会让人误以为是平面直角坐标系中的横纵坐标,最好将参数改名为r和c,表示行列坐标。(3)maze[x][y]表示第x行第y列的坐标点的值,当其取值为0、1、2时分别表示不可通行、可通行、已查找。(4)递归出口:当(x==8 and y==8)时,执行print("successful!"),并返回True。递归体:当valid(maze, x, y)为True时,先设置maze[x][y] = 2,再针对四个方向依次试探,分4次递归调用函数walk。
(5)程序输出了两行“successful!”,说明通过2条独立的路径找到了出口。应该在调用walk函数时判断是否找到出口,若找到出口则直接返回True,停止试探下一方向。可以对walk函数加以改进,使其在找到出口时返回True,否则返回False。然后在主函数中,根据walk函数的返回值决定输出 “successful!”或“failed!”。
(6)walk函数的递归体部分采用顺序结构依次向上左下右四个方向试探,代码有些重复,可以设置一个二维数组dirs,存储分别向上左下右移动的行列坐标变换情况,通过循环遍历dirs,将代码做进一步简化。参考代码如下: dirs = [[-1, 0],[0, -1],[1, 0],[0, 1]] #依次向上左下右四个方向试探,若找到出口,则结束查找 if walk(maze,r+d[0],c+d[1]): return False # 未找到迷宫出口,返回False(7)参考代码如下(仅对walk函数做了修改,其他代码不变):def walk(maze, r, c): #用栈实现深度优先搜索 dirs = [[-1, 0],[0, -1],[1, 0],[0, 1]] st.append([r, c, 0]) #将起点坐标和初始朝向均入栈 r, c, nextd = st.pop() #退栈,并读取栈顶元素的坐标和朝向 for i in range(nextd, 4): #依次检查栈顶元素未探查方向 nextr, nextc = r+dirs[i][0], c+dirs[i][1] if nextr == 8 and nextc == 8: #若找到出口,则结束查找 if valid(maze, nextr, nextc): maze[nextr][nextc] = 2 #做标记,防止折回 st.append([r, c, i+1]) #原位置和其下一方向入栈 st.append([nextr, nextc, 0]) #新位置和初始朝向入栈课后作业
任务(7)通过构造一个栈来解决走迷宫问题的算法被称为深度优先搜索算法,其特点是先沿着一个方向不断向前查找,直到找到终点或此路不通为止,若某位置不通了,则退回上一位置,换个方向继续查找。
除此之外,还有一种被称为广度优先搜索的算法,它通过构造一个队列来存储途径点的坐标,每次查找都先把当前位置的相邻点加入队列,直到找到终点或队列为空。此种算法需要占据较多空间,但是能找到最短路径,效率较高。参考代码如下(仅对walk函数做了修改,其他代码不变),请将缺失的代码补充完整。
def walk(maze, r, c): #用队列实现广度优先搜索
#如果位置是迷宫的出口,说明成功走出迷宫
if r == 8 and c == 8:
return True
from queue import Queue #引入queue模块FIFO队列Queue
q = Queue() #用来记录路径点坐标的队列
#分别向上左下右移动的行列坐标变换情况
dirs = [[-1, 0],[0, -1],[1, 0],[0, 1]]
maze[r][c] = 2 #做标记,防止折回
q.put([r, c]) #将入口位置入列
while not q.emptue():
r, c = q.get()
for i in range(4): #依次检查四个方向
nextr = 填空1
nextc = 填空2
if nextr == 8 and nextc == 8: #若找到出口,则结束查找
return True
if valid(填空3):
maze[nextr][nextc] = 2 #做标记,防止折回
q.put(填空4)
return False
需要本文word文档、源代码和课后思考答案的,可以加入“Python算法之旅”知识星球参与讨论和下载文件,“Python算法之旅”知识星球汇集了数量众多的同好,更多有趣的话题在这里讨论,更多有用的资料在这里分享。
我们专注Python算法,感兴趣就一起来!





