前面几篇中我们通过引入对偶空间来定义张量。实际上，如果不用对偶空间，也可以引入张量，而且可能对工科同学更加友好。

如果没时间细看本文，可以拉到最后看小结。

向量空间和它的对偶空间毕竟是不同的两个空间。其实，我们也可以摆脱对偶空间，在同一个向量空间中讲故事。通过引入类似的概念，那就是 reciprocal basis，这个可以叫逆变基或者互逆基之类的。

1内积空间

首先，假设是的基。但注意，这里基不一定指标准正交基，可以长短不一甚至互不正交，也就是所谓的斜坐标系。

我们知道，笛卡尔在当年引入坐标系的思想（可点击）时，并没有指定直角坐标系，因此，他脑海里如果有坐标系的话，大概也是指一般情况，即斜坐标系。

那问题来了，既然有了好好的直角坐标系，为什么不用呢？偏偏要去用斜角？比如有时候斜角坐标系更方便于表示实际的物理问题。

话不多说，让我们来看一个 2D 斜坐标系的例子，

在斜坐标系下，每一点的坐标不是拉垂线来确定了，而是按平行四边形法则来确定。

中的一个向量，在一组基向量下的表示为，

{\bf v} = \sum_\nolimits{i} v^{i} {\bf e}_i \qquad (1)

也就是说，向量的坐标记为。注意，这里的上标不是幂次。这主要是为了区分协变分量和逆变分量。另外，为了公式的含义更加明确，我们这里不使用爱因斯坦求和约定，而是把求和符合及下标都写出来。

好了，现在有两个向量和，他们能一起搞啥事情呢？除了加加减减之类的好像也搞不了啥大事情啊。为了带来更多活动，我们可以给向量空间引入一些结构，也就是两两一起运算的规则。

虽然没有平面或者三维空间中那么直观，但我们也可以给高维或者抽象的向量空间引入类似概念，比如向量长度，两个向量间的夹角、垂直等。

例如，只要引入内积，就可以实现这些。根据内积的运算规则，我们有

\begin{aligned} \langle \mathbf{u}, \mathbf{v}\rangle=& \langle \sum_\nolimits{i} u^{i}\mathbf{e}_{i}, \sum_\nolimits{j} v^{j} \mathbf{e}_{j}\rangle \\[0.8em] =&\sum_\nolimits{ij} u^{i} v^{j} \langle\mathbf{e}_{i}, \mathbf{e}_{j}\rangle\\[0.8em] =&\sum_\nolimits{ij} u^{i} v^{j} \mathsf{g}_{ij} \end{aligned} \qquad (2)

我们得到一个二次型，由内积的定义可知，最后那行里的构成一个对称矩阵。由于内积是非退化的，因此它是一个可逆矩阵。另外，由于这些基向量未必正交或者单位长度，这个矩阵往往不是单位矩阵。其实是一个张量的分量，就是所谓的度量张量，而物理书里一般喜欢叫成度规张量。

有了这个度量张量，就可以定义向量的长度以及向量的夹角之类的。

定义向量的长度，

|{\bf u}| = \sqrt{{\langle\bf u}, {\bf u}\rangle} = \sqrt{\small{\sum}_\nolimits{ij}\mathsf{g}_{ij} u^{i}u^{j}}

定义两个非零向量的夹角的余弦，

\cos \theta = \frac{\langle{\bf u}, {\bf v}\rangle}{|{\bf u}| \cdot|{\bf v}|}=\frac{\sum_\nolimits{ij}\mathsf{g}_{i j} u^{i} v^{j}}{\sqrt{\sum_\nolimits{ij}\mathsf{g}_{ij} u^{i}u^{j}} \sqrt{\sum_\nolimits{ij}\mathsf{g}_{ij} v^{i} v^{j}}}

这里先把这个张量放一放，继续来看式（2）中的求和项。

逆变基

如果的维度是的话，上面的求和总共有项了。原因在于这里的基向量并不一定两两正交。那么有没有办法缩减求和项的个数呢，比如让它只剩项。

我们先引入另外一组基，，注意现在是上标了。此时，其中一个向量用这组基表示，即。注意，此时的坐标反而用了下标，这都是记法，大家只要按照这个规则即可。然后，再把它代入内积公式，得

\begin{aligned} \langle \mathbf{u}, \mathbf{v}\rangle=& \langle \sum_\nolimits{i} u^{i}\mathbf{e}_{i}, \sum_\nolimits{j} v_{j} \mathbf{e}^{j}\rangle \\[0.8em] =&\sum_\nolimits{ij} u^{i} v_{j} \langle\mathbf{e}_{i}, \mathbf{e}^{j}\rangle \end{aligned}

这好像换汤不换药嘛，貌似仍然是项。但是，这里是两组基，两两之间我们可以来搞一点特殊嘛。怎么个特殊法呢？目标上面已经说了，那就是希望最后只有项。

思路就是选择一组特殊的使得上面的表达式被简化为

\langle \mathbf{u}, \mathbf{v} \rangle = u^{1} v_{1} + u^{2} v_{2} + \cdots + u^{n} v_{n}

怎么做到呢，其实也简单，那就是在给定第一组基的前提下，选第二组基时让它满足如下条件，

\langle {\bf e}^{i}, {\bf e}_{j} \rangle = \delta_{j}^{i} \equiv \begin{cases}1 & \text { if } i=j \\ 0 & \text { if } i \neq j\end{cases} \qquad (3)

有些地方把这个要求称为对偶关系、对偶准则或者对偶原理之类的。

那么小明可能又要提问题了：给定一组基向量的情况下，满足上面对偶关系的第二组基向量一定存在吗？

是的，简单点说，第一个基构成了一个非奇异矩阵，那么它一定存在唯一的逆矩阵，而第二个基就来自这个逆矩阵。

下面用一个平面例子来直观地展示几何关系。因为我们只需要以及。因此，给定和（黑色箭头），我们可以如下构造和两个向量（红色箭头），

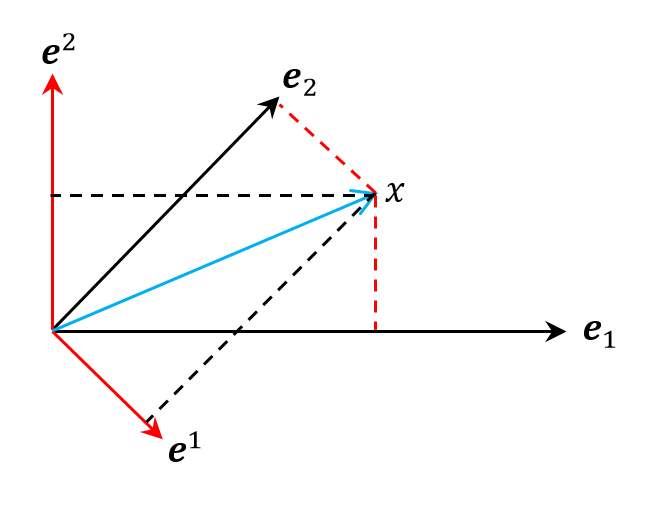
如上图所示，绘制一条垂直于的红线。由于，必须沿着这条线。现在调整的长度直到。然后，用类似方式构建。注意，这里原始的基向量和不一定是单位向量，因此跟它们作内积并不是直接投影。

有了逆变基，我们还可以得到一个向量的协变分量，即

\begin{aligned} \langle\mathbf{x}, \mathbf{e}_{i}\rangle &=\langle x_{1} \mathbf{e}^{1}+x_{2}\mathbf{e}^{2}+\cdots+x_{n} \mathbf{e}^{n}, \mathbf{e}_{i} \rangle \\[0.68em] &=\langle x_{1} \mathbf{e}^{1}, \mathbf{e}_{i} \rangle + \langle x_{2} \mathbf{e}^{2}, \mathbf{e}_{i} \rangle + \cdots + \langle x_{n} \mathbf{e}^{n}, \mathbf{e}_{i} \rangle \\[0.68em] & = x_{i} \end{aligned}

一个向量与原始的基向量内积得到的不是原始基下的坐标，而是它在逆变基下的坐标分量。通过下图我们可以进一步理解上式的几何意义。

但是请注意，为了更好解释几何意义，这里的原始基向量都是单位向量。

同样地，一个向量与逆变基向量的内积得到的不是逆变基下的坐标，而是它在原始基下的坐标分量。

\begin{aligned} \langle \mathbf{x}, \mathbf{e}^{j} \rangle &= \langle \sum_\nolimits{i} x^{i} \mathbf{e}_{i}, \mathbf{e}^{j} \rangle \\[0.68em] &= \langle \sum_\nolimits{i}x^{i} \mathbf{e}^{j}, \mathbf{e}_{i} \rangle \\[0.68em] &=\sum_\nolimits{i}x^{i} \delta_{i}^{j} \\[0.68em] &=x^{j} \end{aligned}

可以看个动画，

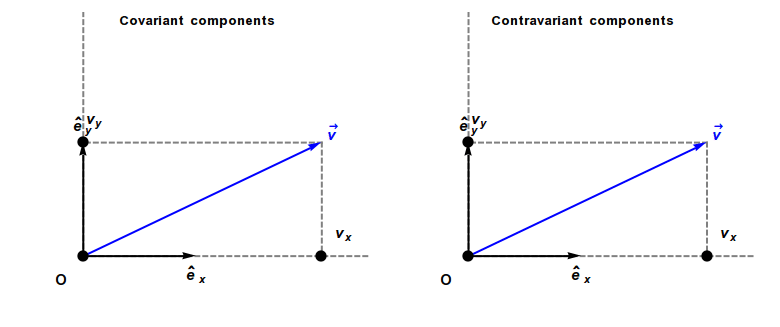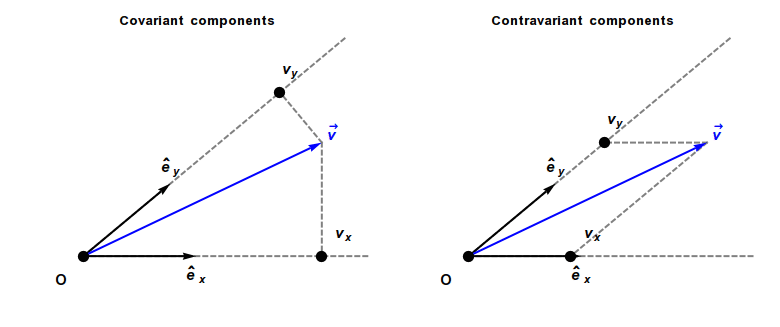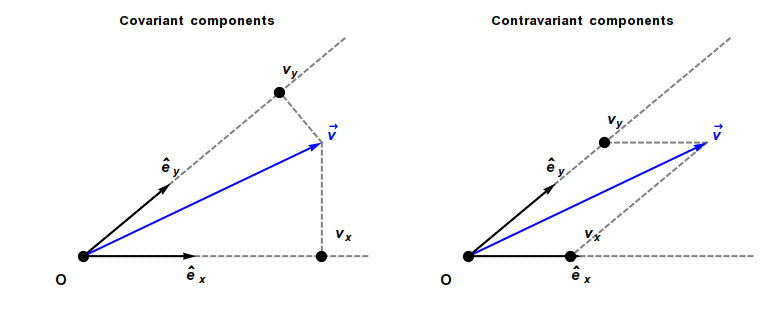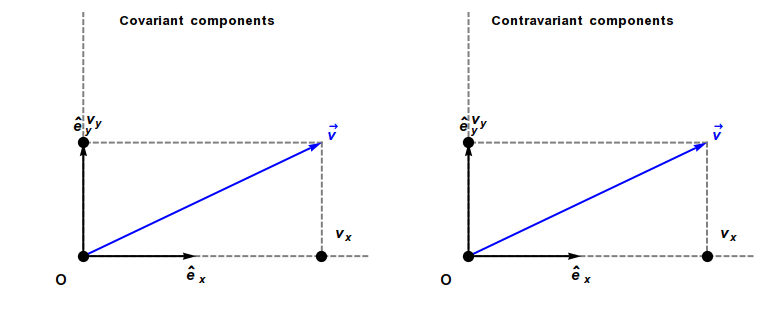
左边是协变分量，右边是逆变分量。感受一下当其中一个原始基向量变动时，向量的不同类型坐标分量是如何跟着变化的。

度量张量的妙用

再回到上面提到的那个度量张量，至于它为什么是一个张量等后面的张量定义吧，我们先承认这点即可。

逆变基向量在原始基上的分解记为，

{\bf e}^{i} = \sum_\nolimits{j} \mathsf{g}^{ij} {\bf e}_{j}

和长得这么相似，是不是有什么关系呢？

将上式代入式 (3)，得

\begin{aligned} \delta_{j}^{i} &= \langle{\bf e}^{i}, {\bf e}_{j}\rangle \\[0.68em] &= \sum_\nolimits{k} \mathsf{g}^{i k} \langle{\bf e}_{k}, {\bf e}_{j} \rangle \\[0.68em] &= \sum_\nolimits{k} \mathsf{g}^{ik} \mathsf{g}_{kj} \end{aligned}

首先，构成一个矩阵。再仔细一看上面式子，它还是度量矩阵的逆矩阵。

这说明什么？说明可以由求得逆矩阵，再根据求得逆变基。

下面我们来看看两个逆变基向量的内积，

\begin{aligned} \langle{\bf e}^{i}, {\bf e}^{j}\rangle &= \langle \sum_\nolimits{k}\mathsf{g}^{ik} {\bf e}_{k}, \sum_\nolimits{l}\mathsf{g}^{jl} {\bf e}_{l}\rangle \\[0.68em] &= \sum_\nolimits{k}\sum_\nolimits{l} \mathsf{g}^{ik} \mathsf{g}^{jl} \langle {\bf e}_{k},{\bf e}_{l}\rangle \\[0.68em] &= \sum_\nolimits{k}\sum_\nolimits{l} \mathsf{g}^{ik} \mathsf{g}^{jl} \mathsf{g}_{kl} \\[0.68em] &= \sum_\nolimits{k}\left(\mathsf{g}^{ik} \sum_\nolimits{l} \mathsf{g}^{jl} \mathsf{g}_{lk} \right) \\[0.68em] &= \sum_\nolimits{k} \mathsf{g}^{ik} \delta_{k}^{j} = \mathsf{g}^{ij} \end{aligned}

其实，如果在上式中只代入一项，推导将变得更加简单，

\begin{aligned} \langle{\bf e}^{i}, {\bf e}^{j}\rangle &= \langle {\bf e}^{i}, \sum_\nolimits{l}\mathsf{g}^{jl} {\bf e}_{l}\rangle \\[0.68em] &= \sum_\nolimits{l} \mathsf{g}^{jl} \langle {\bf e}^{i},{\bf e}_{l}\rangle \\[0.68em] &= \mathsf{g}^{ji} \delta_{i}^{i} = \mathsf{g}^{ij} \end{aligned}

下面再看度量矩阵及其逆矩阵与基向量的运算，会发现一些有趣且实用的规律。

将乘再连加，可得

\begin{aligned} \sum_\nolimits{i} \mathsf{g}_{ij} {\bf e}^{i} &= \sum_\nolimits{i} \mathsf{g}_{ij} \sum_\nolimits{k} \mathsf{g}^{ik} {\bf e}_{k} \\[0.68em] &= \sum_\nolimits{k} \sum_\nolimits{i} \mathsf{g}_{ij} \mathsf{g}^{ik} {\bf e}_{k} \\[0.68em] &= \sum_\nolimits{k} \delta_{j}^{k} {\bf e}_{k} \\[0.68em] &={\bf e}_{j} \end{aligned}

这就是说通过度量矩阵及其逆矩阵实现和之间的相互转换。这很容易记，我们不妨把它们再放一起看看。

{\bf e}^{i} = \sum_\nolimits{j} \mathsf{g}^{ij} {\bf e}_{j}

\begin{aligned} {\bf e}_{j} = \sum_\nolimits{i} \mathsf{g}_{ij} {\bf e}^{i} \end{aligned}

这样，我们得到了内积空间的几个基本量，，，，以及它们之间的关系。这里上下标变来变去貌似有点繁杂，其实有很明显的规律。

小结

我们来理一理思路，揭示一下背后隐藏着的真相。其实我们所考虑的内积空间是由度量张量在背后操控着的。为了以矩阵的形式展示这个张量，我们需要先选定一组基，然后就有了后续。具体展示如下，

给定一组基
设定度量张量在这组基下的协变分量，即
求的逆矩阵
由求逆变基，即

但是，要注意的是，和这两个矩阵不是谁决定谁，而是互逆关系。因此，也可以先给出矩阵。而和是同一个度量张量不同类型的分量，就像和也是同一向量的不同类型的分量那样，即逆变分量和协变分量。

最后，再看一下向量分量的变换规律。我们把代入，得

\begin{aligned} v_i = \langle\mathbf{v}, \mathbf{e}_{i} \rangle &= \langle \sum_\nolimits{k} v^{k} \mathbf{e}_{k}, \sum_\nolimits{j} \mathsf{g}_{ij} {\bf e}^{j} \rangle \\[0.68em] &= \sum_\nolimits{k} \sum_\nolimits{j} v^{k} \mathsf{g}_{ij} \langle \mathbf{e}_{k},{\bf e}^{j} \rangle \\[0.68em] &= \sum_\nolimits{k} \sum_\nolimits{j} v^{k} \mathsf{g}_{ij} \delta_{k}^{j} \\[0.68em] &= \sum_\nolimits{j} \mathsf{g}_{ij} v^{j} \end{aligned}

另一个也同理，放在一起方便观摩，

v^{i} = \sum_\nolimits{j} \mathsf{g}^{ij} v_{j}, \quad v_{i}= \sum_\nolimits{j} \mathsf{g}_{ij} v^{j}

看到了吧，这个度量张量的不同类型的分量可以起到升降分量指标的作用，这在张量计算中是常用的招术。

+放一起欣赏

\{\mathsf{g}_{ij}\} \quad \Longleftrightarrow \quad \{\mathsf{g}^{ij}\}

\langle {\bf e}^{i}, {\bf e}_{j} \rangle = \delta_{j}^{i} \equiv \begin{cases}1 & \text { if } i=j \\ 0 & \text { if } i \neq j\end{cases}

{\bf e}^{i} = \sum_\nolimits{j} \mathsf{g}^{ij} {\bf e}_{j}，\quad {\bf e}_{j} = \sum_\nolimits{i} \mathsf{g}_{ij} {\bf e}^{i}

v_{i} = \langle\mathbf{v}, \mathbf{e}_{i} \rangle, \quad v^{i} = \langle\mathbf{v}, \mathbf{e}^{i} \rangle

v^{i} = \sum_\nolimits{j} \mathsf{g}^{ij} v_{j}, \quad v_{i} = \sum_\nolimits{j} \mathsf{g}_{ij} v^{j}

最后，小明又要提问了，说逆变基与以前说过的对偶基是什么关系呢？

其实呢，有些书也把逆变基称为对偶基，这是叫法问题。但对偶基是在的对偶空间里的，逆变基毕竟还是在同一个向量空间之内的，因此这两者还是要区分的，具体关系我们后续再议。

相关阅读

什么是张量？你躺平一下就知道了

张量之对偶空间，对偶到底是个啥？

张量前传 - 通过向量的并矢积认识张量

矩阵和线性代数原来是这么来的

矩阵特征值的故事 - 缘起琴弦

二次型和矩阵合同原来是这么一回事

矩阵特征值是这么来的，以及有趣的盖尔圆

万能的 SVD 分解是哪位牛人提出来的？

度量、范数和内积原来是这么个关系

线性映射: 从凯莱引入矩阵乘法说起

矩阵之芯 SVD: 奇异值分解及其几何解释

矩阵之芯 SVD: 基本应用以及与其他分解的关系

矩阵之芯 SVD: 从奇异值分解看四个基本子空间

矩阵之芯 SVD: 从奇异值分解 SVD 看 PCA

不提对偶空间也能讲好张量故事