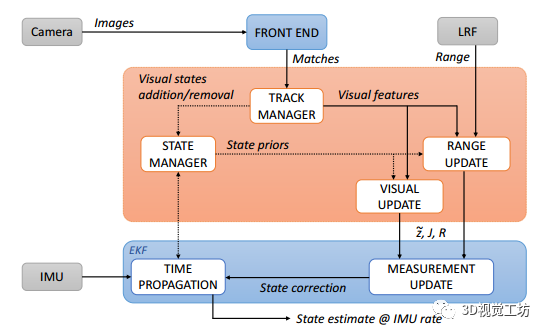
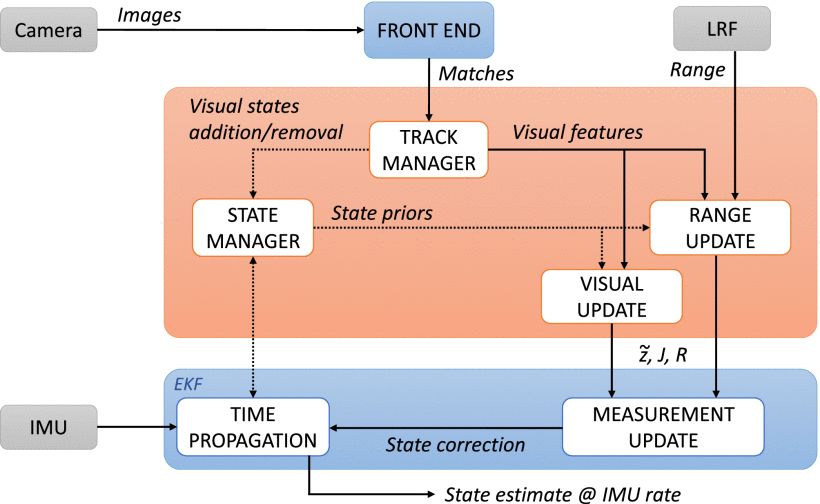
距离-视觉-惯性里程计:无激励的尺度可观测性(ICRA2021)
代码、论文地址:在公众号「3D视觉工坊」,后台回复「尺度可观测性」,即可直接下载。








原创征稿
3D视觉工坊是基于优质原创文章的自媒体平台,创始人和合伙人致力于发布3D视觉领域最干货的文章,然而少数人的力量毕竟有限,知识盲区和领域漏洞依然存在。为了能够更好地展示领域知识,现向全体粉丝以及阅读者征稿,如果您的文章是3D视觉、CV&深度学习、SLAM、三维重建、点云后处理、自动驾驶、三维测量、VR/AR、3D人脸识别、医疗影像、缺陷检测、行人重识别、目标跟踪、视觉产品落地、硬件选型、求职分享等方向,欢迎砸稿过来~文章内容可以为paper reading、资源总结、项目实战总结等形式,公众号将会对每一个投稿者提供相应的稿费,我们支持知识有价!
▲长按关注公众号
评论
