破解千年数学谜题：如何寻找奇数「完全数」？

---

  新智元报道  

来源：quantamagazine

编译：小匀

世间都有哪些堪称完美的事物？

是达芬奇笔下蒙娜丽莎的微笑，还是1984年洛杉矶奥运会体操赛场上，雷顿的10分的完美成绩，亦或歌后玛丽亚·凯莉的动人音乐？

这些都是完美的，在数学届，也有此类事物——6与28。

对于艺术性和运动性，完美在于观察者的眼睛。

但对于数字来说，完美则由数学来定义。

何为完全数（Perfect numbers）？

完全数等于其正因数之和。

例如，6的正因数有3，2，1，而6=3+2+1；

当然，还有28。28=14+7+4+2+1。

2000多年前，古希腊数学家欧几里德在就提出了完全数的基本原理，他知道最初的四个完全数是6、28、496和8128。

从那时起，又发现了许多完全数。

但奇怪的是，它们都是偶数。

经过几千年的寻找未果，也没人找到一个奇数完全数，因此，「奇数完全数不存在」的结论被认定了。

但数学家也没能证明这一点。

为什么我们可以对偶数完全数了解这么多，却无法回答一个最简单的奇数问题？现代数学家又是如何解决这个古老的问题的呢？

我们对数学完美性的探索是从除数(Divisor)开始的。

我们知道6是12的除数，因为12／6=2；再比如，25是100的除数，因为100／25=4。

前面我们已经知道，一个数如果等于它的除数之和时，我们说他是「完全数」，除数是小于这个数本身。

我们也可以定义一个数为完美的，当它的所有除数之和，真因子和非真因子之和，是这个数的两倍。

这是因为一个数唯一不是真因子的除数就是这个数本身。

完全数（Perfect number），又称完美数或完备数，是一些特殊的自然数。它所有的真因子（即除了自身以外的约数）的和（即因子函数），恰好等于它本身。

根据这个定义，28仍然是完美的：它的真因子是1，2，4，7和14，它的真因子是28，它的所有因子之和，1+2+4+7+14+28，是56，也就是2×28。

包含非真因子除数的和对于要用完美数做的一些代数来说是很方便的。

在处理完全数的时候，我们会经常说「一个数的除数之和」，所以数学家把它变成了一个函数。

我们定义σ(n)，或者说「n的Σ」，是n的除数之和。

我们已经知道，σ(28)=56，σ(1)=1，σ(6)=1+2+3+6=12，σ(10)=1+2+5+10=18。

但请注意，6是一个完美的数字，因为σ(6)=2×6，但1和10不是。

这个函数σ有一些特殊的性质，适合研究完美数。

定义具备，只差数学工具。

我们应该从哪里开始找？

素数（primes）。

根据定义，一个素数只能被它自己和1整除。这使得素数的σ计算变得非常容易：σ(2)=1+2=3，σ(3)=1+3=4，σ(5)=1+5=6，σ(7)=1+7=8。一般来说，对于任何素数p，σ(p)=1+p。

素数能不能是完全数？只有当σ(p)=1+p=2p时，才会如此。

代数知识告诉我们，只要p=1，上述就会成立，但由于素数的定义是大于1的，所以没有一个素数可以是完美的。

所以，素数不可能是完美的。

那下一步该怎么办？

让我们把目光落在素数的幂（power）上，比如。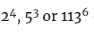

考虑像16或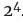这样的素数幂。24的除数只有2的2的4次方：

。

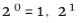
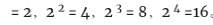所以σ(24)可以这样计算：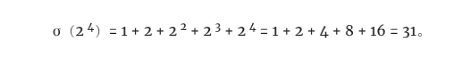

对于任何素数幂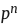

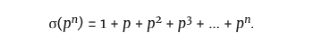
如果我们使用代数课上的一个公式，这就变得更加简单了。请注意，σ(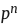)中的每项加起来都是前一项的p倍。这使得其成为一个几何数列，而几何数列的和有一个很好的公式：

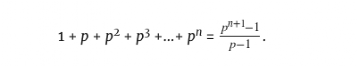
由于有了几何级数公式，我们不必列出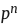的所有除数来计算σ(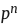)。我们可以直接使用公式：

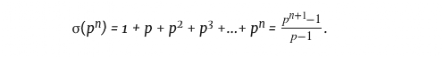
例如，我们已经看到，

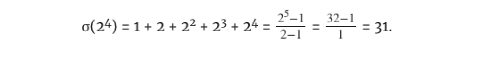
而我们只要把其他素数的除数插入公式中，就可以计算出它们的除数之和，

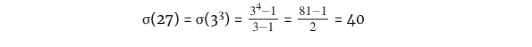
还有，

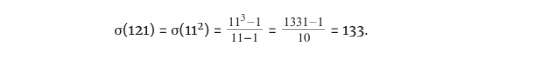
请注意，这些素数都不满足「完全数」的条件，

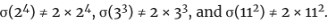
事实上，没有一个素数可以是完美的。为了得到一个「完全数」，我们需要σ(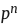)=2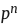，这就意味着，

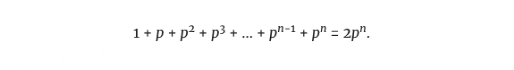
我们可以从方程的两边减去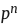，得到，

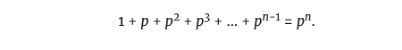
现在我们就用几何级数公式来计算这个方程的左边。由于

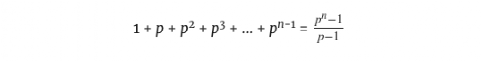
我们得到

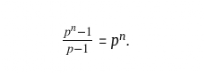
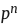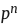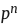我们需要上述为真，才是「完全数」。但是请注意， - 1比小，用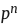 - 1除以p - 1会使其更小，所以，

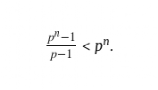
因此，没有一个素数幂是「完全数」。

所以没有完美的素数，也没有完美的素数幂。什么可以是完美的？嗯，我们知道28是完美的，它是两个不同素数的乘积。

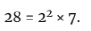
任何不是素数或素数幂的数都可以写成不同素数幂的乘积，就像这样。而这些因式化，再加上函数σ的一个特殊性质，可以帮助我们判断一个数是否完美。

我们已经知道σ(28)=1+2+4+7+14+28，但我们再仔细看看这个和。请注意，最后三个数字都是7的倍数。

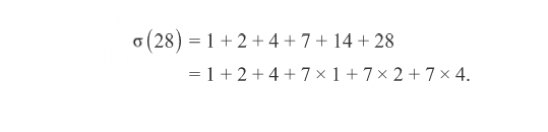
我们可以将这7个因素计算出来，以揭示一些隐藏的结构，

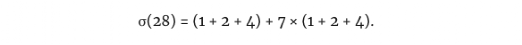
再加上一些更巧妙的分布特性因子，我们可以写出，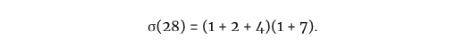

这并没有告诉我们任何我们不知道的事情：σ(28)=(1+2+4)(1+7)=7×8=56，这证实了28是完美的。但是在这个乘法里面还隐藏着一些重要的东西，

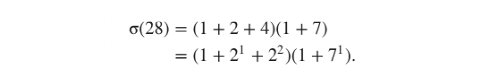
括号中的那些表达式看起来很熟悉：1+21+22=σ(22)，1+71=σ(7)。这意味着我们实际上可以写出，

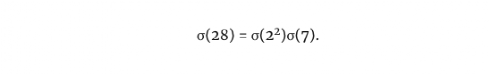
为了计算σ(28)=σ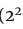×7)，我们其实可以计算σ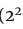)和σ(7)，并将它们相乘。这是一个惊喜，一般情况下都是如此。任何时候，你把一个数字分解成这样的素数， 你都可以用这个捷径来计算σ。例如，由于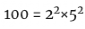，我们可以这样计算σ(100)：

这比把100的9个被除数全部列出并加起来要简单一些。

为什么会这样呢？一个数的除数来自于它的质因数。再考虑28，它是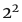和7的乘积，再想想下面的乘法表：

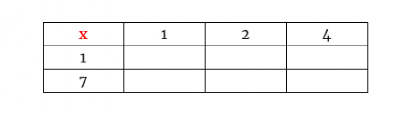
沿着上边是2的幂，可以均匀地除以28，下边是7的幂，可以均匀地除以28。注意，当我们填好这张乘法表后，会发生什么事情呢？

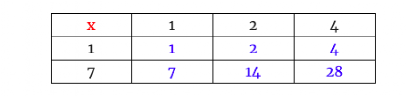
我们得到28的所有除数。这是因为28的每一个被除数都是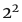和7的被除数的组合，是28的因式化中出现的素数。

现在将乘法表与表达式进行比较：

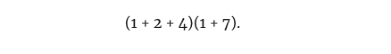
当我们用分配性质将其乘出时，也就产生了28的所有被除数，然后将其相加。

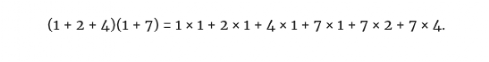
换句话说，(1＋2＋4)(1＋7)正好是σ(28)。但(1+2+4)(1+7)也是σ(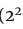)σ(7)。所以σ(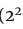)σ(7)=σ(28)。这个例子证明了一个关于σ的非常有用的事实。在数论的语言中，这个函数是 "乘法 "的。

这意味着，只要数字a和b是「互素」（relatively prime），即它们没有共同的因数，σ(ab)=σ(a)σ(b)。

这就是σ的特殊功能，它非常适合帮助我们研究完全数。欧几里德在两千年前就利用这个事实，在一种特殊的素数和关于乘积和除数的巧妙论证的帮助下，创造了一个求完全数的公式。这样一来，他就迈出了第一步，确定了每一个偶数完全数的样子。让我们看看他是如何做到的。

首先，请注意，对于任何2的幂，我们有

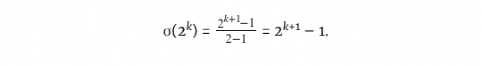
这是我们前面讨论的几何数列公式的结果。现在考虑下面的思想实验。如果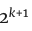-1是素数呢？

好了，由于σ(p)=1+p，对于任何素数，我们知道σ(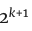 - 1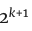)=1+- 1=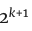。并且注意到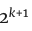正好是2k的两倍，因为指数定律说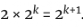。所以我们在数字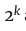和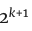 - 1之间有以下两个有趣的关系。

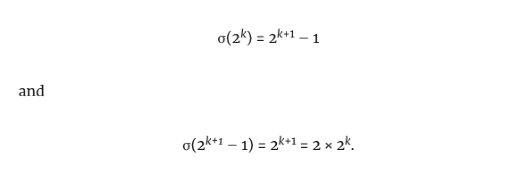
欧几里得注意到一个巧妙的方法来利用这些关系。他把这两个数放在一起，使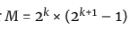，只要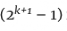是素数，这个数就是完美的！为了看清这一点，我们要计算σ(M)，证明它等于2M。

首先，请注意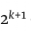- 1比偶数少一个，所以它一定是奇数，这意味着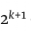- 1不能被2整除。这意味着 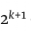- 1不能被2整除，但2k只能被2的幂整除，所以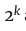和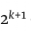- 1没有公因数，因此是「互素」。

这样我们就可以利用σ的乘法性质。

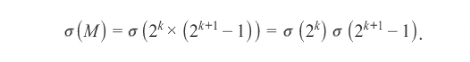
我们已经知道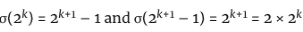，所以可以找到σ(M)。

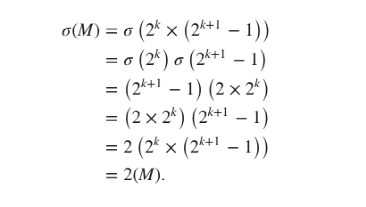
所以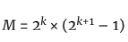，是完美的。

请记住，这依赖于一个假设，即数字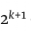 - 1是素数。这些数字被称为梅森素数，你可能听说过它们，因为互联网梅森素数大搜索(GIMPS)，这是一个寻找巨大的梅森质数的在线计算合作努力。每当你听到一个新的最大素数的发现，它可能是GIMPS的结果。而且由于欧几里德的证明，只要发现一个新的梅森素数，就会发现一个新的完美数。

例如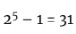，是梅森素数，所以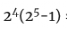= 16×31 = 496是一个完全数。另外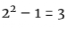，是梅森素数，所以 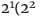- 1) = 2 × 3 = 6 是完全数。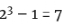是梅森素数，所以 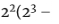 1) = 4 × 7 = 28 是完全数。

你可能已经注意到，这些完全数都是偶数。这是有道理的，因为只要k>0，数字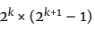就会是偶数。而如果k = 0，那么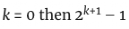就是1，这不是素数）。

你可能也注意到了，到目前为止我们所讨论的所有完全数似乎都涉及到梅森素数。这并不是巧合：在欧几里得表明这个公式可以产生完全数的2000年后，Leonhard Euler证明了这是获得偶数完全数的唯一方法。但是，奇数完全数可能是什么样子（如果存在的话）的问题仍然没有解决。

而今天它仍然开放。虽然他们找不到，但数学家们有很多信息，关于一个假设的奇数完全数可能是什么样子的。它不可能被105所整除 它至少要有九个不同的质因数 其中第二大质因数要大于10000个 而且当它被12除以12时，必须有1的余数，或者当它被36除以36时，必须有9的余数。

要证明关于可能根本不存在的数字的结果，这可能看起来很奇怪。但每一条新规则都会使搜索范围更窄一些。如果他们幸运的话，数学家可能会证明奇数必须满足两个不相容的标准，这将一劳永逸地证明没有奇数存在。

为了寻找不相容的标准，数学家甚至开始研究那些并不完美的数字。一个 "恶搞完美数 "是一个看起来很完美的数字，如果你假装它的一个非素数因子实际上是素数。例如，60，3，4和5的乘积，可以被认为是 「spoof perfect number」。如果你假设它的因式中的4是素数，那么我们开发的σ的捷径就会给我们带来：

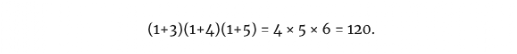
如果σ(60)等于120，那么60就完美了。当然，σ(60)实际上并不等于120，但如果我们假设4是一个素数，它看起来就像它。这就是为什么它是一个「恶作剧」。

花几千年时间去猎取具有奇特性质的数，证明那些可能根本不存在的物体的定理，发明新的甚至更奇怪的数的世界去探索，这似乎很奇怪。但对于一个数学家来说，这是很有意义的。

参考资料：

https://www.quantamagazine.org/the-mysterious-math-of-perfect-numbers-20210315/