所以,机器学习和深度学习的区别是什么?
↑↑↑点击上方蓝字,回复资料,10个G的惊喜
作者:aporras 翻译:郭振@Python与算法社区(ID:alg-channel)
深度学习是机器学习算法的子类,其特殊性是有更高的复杂度。因此,深度学习属于机器学习,但它们绝对不是相反的概念。我们将浅层学习称为不是深层的那些机器学习技术。
让我们开始将它们放到我们的世界中:

这种高度复杂性基于什么?
在实践中,深度学习由神经网络中的多个隐藏层组成。我们在《从神经元到网络》一文中解释了神经网络的基础知识,然后我们已经将深度学习介绍为一种特殊的超级网络:
层数的增加和网络的复杂性被称为深度学习,类似于类固醇(steroids)上的常规网络。
为什么这种复杂性是一个优势?
知识在各个层间流动。就像人类学习,一个逐步学习的过程。第一层专注于学习更具体的概念,而更深的层将使用已经学习的信息来吸收得出更多抽象的概念。这种构造数据表示的过程称为特征提取。
它们的复杂体系结构为深度神经网络提供了自动执行特征提取的能力。相反,在常规的机器学习或浅层学习中,此任务是在算法阶段之外执行的。由人员,数据科学家团队(而非机器)负责分析原始数据并将其更改为有价值的功能。
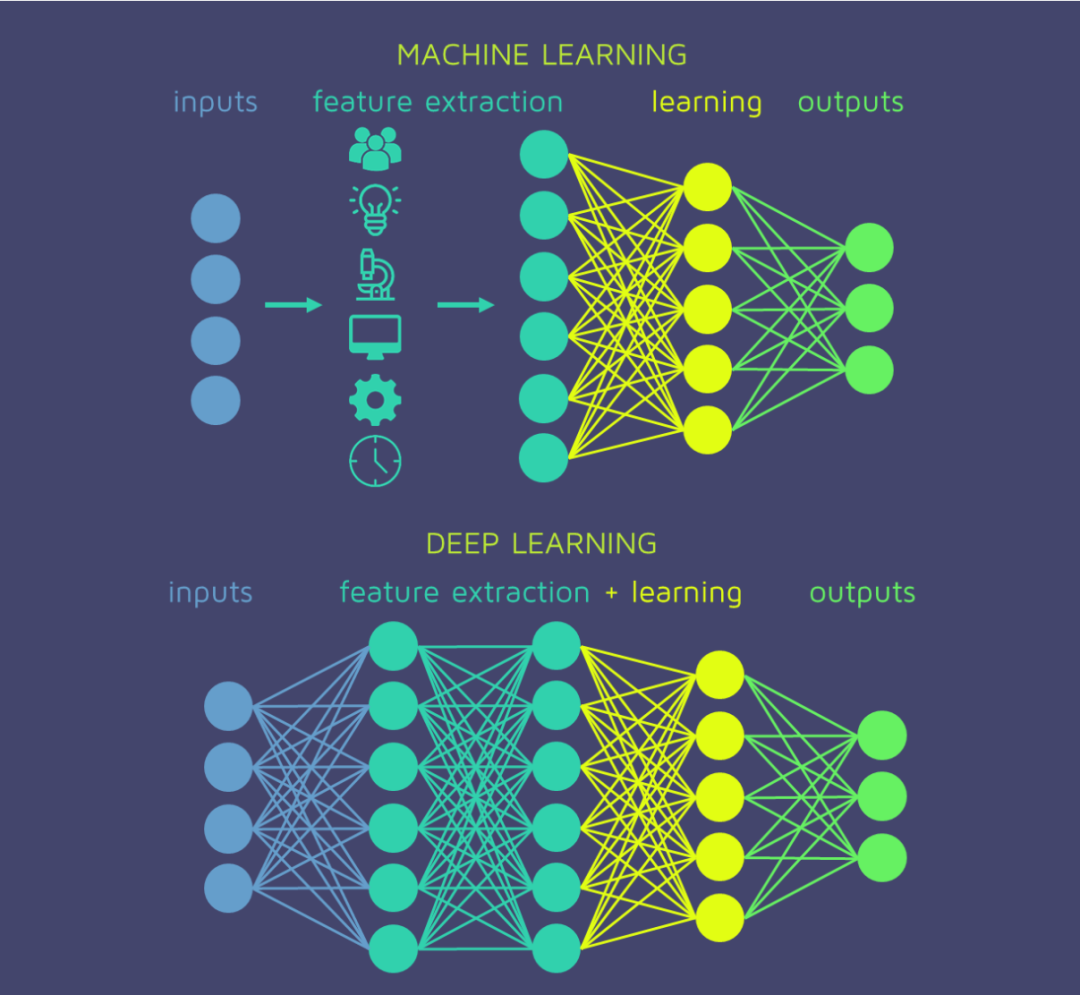
深度学习的根本优势在于,可以在无结构化数据上训练这些算法,而无限制地访问信息。这种强大的条件为他们提供了获得更多有价值的学习的机会。
也许现在您在想...
从多少层开始,它被视为深度学习?关于浅层学习何时结束和深度学习何时开始尚无统一定义。但是,最一致的共识是,多个隐藏层意味着深度学习。换句话说,我们考虑从至少3个非线性转换进行深度学习,即大于2个隐藏层+ 1个输出层。
除了神经网络之外,还有其他深度学习吗?
我也无法对此达成完全共识。然而,似乎有关深度学习的一切至少或间接地与神经网络有关。因此,我同意那些断言没有神经网络就不会存在深度学习的人的观点。
我们什么时候需要深度学习?
通用逼近定理( Universal Approximation Theorem, UAT)声明,只有一个有限层神经元的隐藏层足以逼近任何寻找的函数。这是一个令人印象深刻的陈述,其原因有两个:一方面,该定理证明了神经网络的巨大能力。但是,另一方面,这是否意味着我们永远不需要深度学习?不,深吸一口气,并不意味着……
UAT并未指定必须包含多少个神经元。尽管单个隐藏层足以为特定函数建模,但通过多个隐藏层网络学习它可能会更加有效。此外,在训练网络时,我们正在寻找一种函数,可以最好地概括数据中的关系。即使单个隐藏网络能够表示最适合训练示例的函数,这也不意味着它可以更好地概括训练集中数据的行为。
Ia Goodfellow,Yahua Bengio,Aaron Courville的《深度学习》一书对此进行了很好的解释:
总而言之,具有单层的前馈网络足以表示任何函数,但是该层可能过大而无法正确学习和概括。在许多情况下,使用更深入的模型可以减少表示函数所需的单元数,并可以减少泛化误差。
总结
深度学习基本上是机器学习的子类,它是使用多个隐藏层的神经网络。它们的复杂性允许这种类型的算法自行执行特征提取。由于它们能够处理原始数据,因此可以访问所有信息,因此有可能找到更好的解决方案。
原文链接:https://quantdare.com/what-is-the-difference-between-deep-learning-and-machine-learning/
也可以加一下老胡的微信 围观朋友圈~~~
推荐阅读
(点击标题可跳转阅读)
老铁,三连支持一下,好吗?↓↓↓
