巧妙算法背后的直觉：浅谈贝叶斯优化之美-技术圈

编译 | 蒋宝尚

编辑 | 陈彩娴

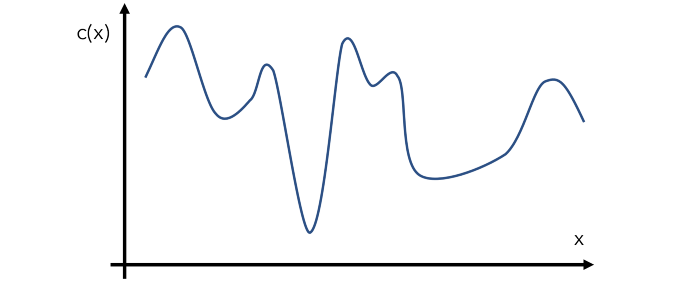
假设有一个函数F(x)，已知计算成本很高，且解析式和导数未知。问：如何找到全局最小值？

毫无疑问，这是一个非常烧脑的任务，比机器学习所有的优化问题都烧脑，毕竟机器学习中的梯度下降就默认了导数可得。

在其他优化问题下，能够采用的方法非常多，即使不用梯度下降，粒子群或模拟退火等非梯度优化方法也是解决方案之一。

再者，如果能够以较低的计算成本得到输入变量x的结果，那么也能够用简单的网格搜索，从而得到良好的效果。

显然，开头提到的问题并不具备这些条件，主要来说有以下几方面的限制：

1、计算昂贵。我们的优化方法必须在有限的输入采样的条件下工作。

2、导数未知。梯度下降以及它的各种变体仍然是深度学习中最受欢迎的方法，而梯度下降必须要求导数条件可得。其实，有了导数，优化器也有了方向感。可惜，本题导数不可得。

3、任务目标是全局最优值。这一任务即使把条件放宽到导数可知，也是非常困难的。所以，我们需要一种机制来避免陷入局部最小值。

如此困难，那么有没有解决方法？有的！它的名字叫做：贝叶斯优化。它能够有效克服上述难点，并且试图用最少的步骤找到全局最小值。

贝叶斯优化之美

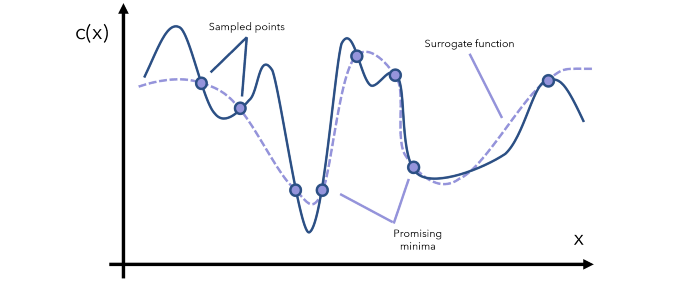
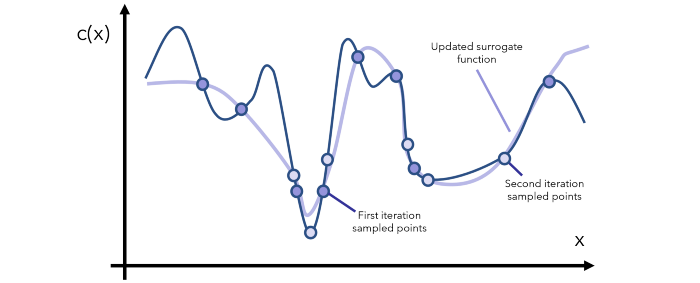
先构建一个函数C(x)，描述了在给定输入x的情况下的成本开销。在行话术语里，这一函数也叫作 "目标函数"，一般来说C(x)的表达式会隐藏在优化器之中。

而贝叶斯优化是通过寻找“替代函数”完成任务，替代函数替代一词指的是目标函数的近似。利用采样点形成的替代函数，如上图所示：

有了替代函数，我们就可以确定哪些点是最有希望的全局最小值，然后“希望的区域”里抽取更多的样本，并相应的更新替代函数。

每一次迭代，都会继续观察当前的替代函数，通过采样了解更多有希望的区域，并及时更新函数。值得一提的是，替代函数选择的原则是“便宜”，例如y=x就是成本非常高的替代函数， y=arcsin((1-cos²x)/sin x)则在某些情况下比较便宜。

经过一定次数的迭代后，肯定会找到全局最小值。如果找不到，那么函数的形状肯定非常奇怪(例如上下波动的幅度非常大)，所以，在这种情况下，应该问一个比优化更好的问题：数据有什么问题？

显然，用替代函数的方法，满足了开头的三个条件：1.计算便宜；2.解析式不知；3.导数不知。

高斯分布表示替代函数

那么，为什么用替代函数的方法成为了贝叶斯优化呢？

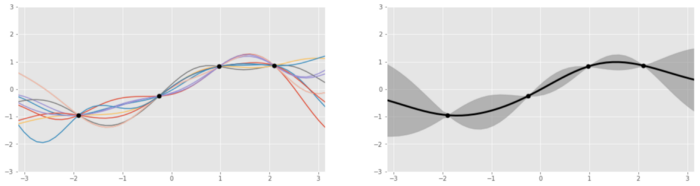
其实，贝叶斯统计和建模的本质是根据新的信息更新先验信念(prior belief) ，然后产生后验信念(posterior belief)。

另外，替代函数通常由高斯过程表示。更形象一些，可以用骰子类比，只不过投掷出去之后，返回的是一些函数（例如sin、log），而不是1~6的数字。这些函数能够拟合给定的数据，并且以某种概率被“掷”出来。

左：四个数据点的几个高斯过程生成的函数；将四个函数聚合之后的函数。

那么，为什么使用高斯分布，而不用其他什么的曲线进行拟合建模替代函数？其中一个理由是：高斯分布具有贝叶斯性质。高斯过程作为一种概率分布，是事件最终结果的分布，包含了所有可能的函数。

例如，我们先将当前的数据点集合可由函数a(x)和b(x)表示。其中，满足a(x)的占比为40%，满足b(x)的占比为10%。然后将替代函数表示为概率分布时，可以通过固有的概率贝叶斯过程，用新信息进行更新。或许当引入新信息时，满足a(x)的数据变为20%，这种变化由贝叶斯公式控制。

替代函数（先验）会被更新为习得函数（acquisition function），习得函数会在开发（Exploitation）和勘探（Exploration）之间做权衡。其中，开发是指的在模型预测的目标好的地方进行采样，也就是利用已知的有希望的区域。但是，如果已经对某一区域进行了足够的开发，那么继续利用已知的信息就不会有什么收获。

勘探指的是在不确定性高的地方进行采样，这能查缺补漏，因为有可能全局最小值可能恰好就在之前没有注意到的地方。

如果习得函数鼓励更多的开发，比较少的探索，这会导致模型可能陷入局部最小值。相反，如果鼓励探索，抑制开发，模型可能在最开始会略过全局最小值。所以，采集函数试图找到微妙的平衡，才能产生良好的结果。

习得函数，必须同时考虑开发和探索。常见的习得函数包括预期改进和最大改进概率，所有这些函数都是在给定先验信息（高斯过程）的情况下，衡量特定投入在未来可能得到回报的概率。

总结

基于以上，总结下贝叶斯优化的执行方式：

1、初始化一个高斯过程 "替代函数 "的先验分布

2、选择几个数据点x，在当前先验分布上运行的习得函数a(x)最大化。

3、评估目标成本函数c(x)中的数据点x，得到结果y。

4、用新的数据更新高斯过程先验分布，以重复步骤2-5进行多次迭代。

5、产生一个后验（它将成为下一步的先验）

6、解释当前的高斯过程分布，从而找到全局最小值。

贝叶斯优化就是概率论的思想和替代优化思想的结合。这两种思想的结合已经有了很多应用，从医药产品开发到自动驾驶汽车都能看到它的身影。

但在机器学习中，最常见的是贝叶斯优化是用于超参数优化。但其他计算评估输出比较昂贵的场景也同样适用。

转自：AI科技评论