【机器学习基础】分类算法之贝叶斯网络-技术圈

↑↑↑点击上方蓝字，回复资料，10个G的惊喜

贝叶斯网络

马尔科夫链描述的是状态序列，很多时候事物之间的相互关系并不能用一条链串起来，比如研究心血管疾病和成因之间的关系便是如此错综复杂的。这个时候就要用到贝叶斯网络：每个状态只跟与之直接相连的状态有关，而跟与它间接相连的状态没直接关系。但是只要在这个有向图上，有通路连接两个状态，就说明这两个状态是有关的，可能是间接相关。状态之间弧用转移概率来表示，构成了信念网络（Belief Network）。
贝叶斯网络的拓扑结构比马尔可夫链灵活，不受马尔科夫链的链状结构的约束，更准确的描述事件之间的相关性。马尔科夫链是贝叶斯网络的一个特例，而贝叶斯网络是马尔科夫链的推广。
拓扑结构和状态之间的相关概率，对应结构训练和参数训练。贝叶斯网络的训练比较复杂，从理论上讲是一个NP完备问题，对于现在计算机是不可计算的，但对于某些具体应用可以进行简化并在计算机上实现。

对于贝叶斯学派，首先想到的就是后验概率公式和先验分布，认为所有的变量都是随机的，有各自的先验分布。我想贝叶斯网络是可以帮助医生进行诊断决策的，前段时间研究过的compressive tracking就是采用的朴素贝叶斯分类器，我对与贝叶斯相关内容的应用就是从此开始有所了解的。朴素贝叶斯分类有一个限制条件，就是特征属性必须有条件独立或基本独立（实际上在现实应用中几乎不可能做到完全独立）。当这个条件成立时，朴素贝叶斯分类法的准确率是最高的，但不幸的是，现实中各个特征属性间往往并不条件独立，而是具有较强的相关性，这样就限制了朴素贝叶斯分类的能力。这里讨论的就是贝叶斯分类中更高级、应用范围更广的一种算法——贝叶斯网络（又称贝叶斯信念网络或信念网络）。

一个贝叶斯网络定义包括一个有向无环图（DAG）和一个条件概率表集合。DAG中每一个节点表示一个随机变量，可以是可直接观测变量或隐藏变量，而有向边表示随机变量间的条件依赖；条件概率表中的每一个元素对应DAG中唯一的节点，存储此节点对于其所有直接前驱节点的联合条件概率。

贝叶斯网络有一条极为重要的性质，就是我们断言每一个节点在其直接前驱节点的值制定后，这个节点条件独立于其所有非直接前驱前辈节点。

这个性质很类似Markov过程。其实，贝叶斯网络可以看做是Markov链的非线性扩展。这条特性的重要意义在于明确了贝叶斯网络可以方便计算联合概率分布。一般情况先，多变量非独立联合条件概率分布有如下求取公式：

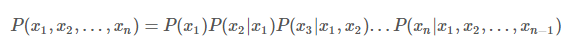
而在贝叶斯网络中，由于存在前述性质，任意随机变量组合的联合条件概率分布被化简成

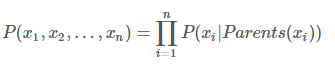
其中Parents表示xi的直接前驱节点的联合，概率值可以从相应条件概率表中查到。

如果没有前驱结点，就用先验概率带入。就这样能够计算出所有的相关或者间接相关的变量的联合概率密度，知道了联合概率密度，对于边缘概率密度的计算就非常简单了，通过这个能够形成一些有意义的推理，等效于生成了知识。

贝叶斯网络比朴素贝叶斯更复杂，而想构造和训练出一个好的贝叶斯网络更是异常艰难。但是贝叶斯网络是模拟人的认知思维推理模式，用一组条件概率函数以及有向无环图对不确定性的因果推理关系建模，因此其具有更高的实用价值。

贝叶斯网络在词分类中的应用

使用贝叶斯网络建立一个文章、关键词和概念之间的联系。
2002年google工程师们利用贝叶斯网络建立了文章、关键词和概念之间的联系，将上百万关键词聚合成若干概念的聚类，称之为phil cluster。最早的应用是广告的拓展匹配。

实际上我觉得这个应用他讲的并不清楚，我是理解不好。

不如借用《算法杂货铺——分类算法之贝叶斯网络(Bayesian networks)》中的例子说明一下。

SNS社区中不真实账号的检测

在那个朴素贝叶斯分类器的解决方案中，我做了如下假设：
i、真实账号比非真实账号平均具有更大的日志密度、更大的好友密度以及更多的使用真实头像。
ii、日志密度、好友密度和是否使用真实头像在账号真实性给定的条件下是独立的。
但是，上述第二条假设很可能并不成立。一般来说，好友密度除了与账号是否真实有关，还与是否有真实头像有关，因为真实的头像会吸引更多人加其为好友。因此，我们为了获取更准确的分类，可以将假设修改如下：
i、真实账号比非真实账号平均具有更大的日志密度、更大的好友密度以及更多的使用真实头像。
ii、日志密度与好友密度、日志密度与是否使用真实头像在账号真实性给定的条件下是独立的。
iii、使用真实头像的用户比使用非真实头像的用户平均有更大的好友密度。
上述假设更接近实际情况，但问题随之也来了，由于特征属性间存在依赖关系，使得朴素贝叶斯分类不适用了。既然这样，我去寻找另外的解决方案。
下图表示特征属性之间的关联：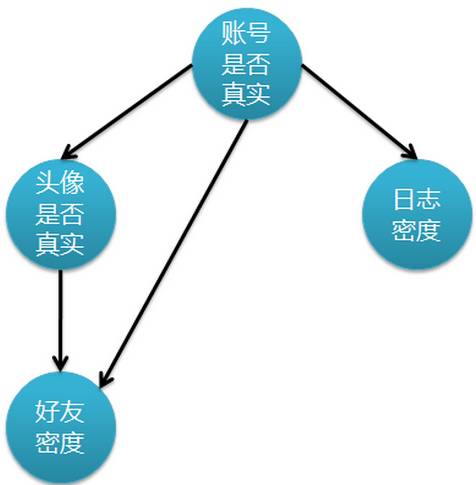

上图是一个有向无环图，其中每个节点代表一个随机变量，而弧则表示两个随机变量之间的联系，表示指向结点影响被指向结点。不过仅有这个图的话，只能定性给出随机变量间的关系，如果要定量，还需要一些数据，这些数据就是每个节点对其直接前驱节点的条件概率，而没有前驱节点的节点则使用先验概率表示。
例如，通过对训练数据集的统计，得到下表（R表示账号真实性，H表示头像真实性）：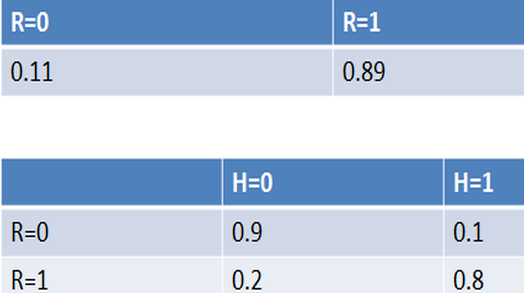

纵向表头表示条件变量，横向表头表示随机变量。上表为真实账号和非真实账号的概率，而下表为头像真实性对于账号真实性的概率。这两张表分别为“账号是否真实”和“头像是否真实”的条件概率表。有了这些数据，不但能顺向推断，还能通过贝叶斯定理进行逆向推断。例如，现随机抽取一个账户，已知其头像为假，求其账号也为假的概率：

也就是说，在仅知道头像为假的情况下，有大约35.7%的概率此账户也为假。如果觉得阅读上述推导有困难，请复习概率论中的条件概率、贝叶斯定理及全概率公式。如果给出所有节点的条件概率表，则可以在观察值不完备的情况下对任意随机变量进行统计推断。上述方法就是使用了贝叶斯网络。

SNS社区中不真实账号检测模型中存在四个随机变量：账号真实性R，头像真实性H，日志密度L，好友密度F。其中H，L，F是可以观察到的值，而我们最关心的R是无法直接观察的。这个问题就划归为通过H，L，F的观察值对R进行概率推理。推理过程可以如下表示：

使用观察值实例化H,L和F，把随机值赋给R。
计算P(R|H,L,F)=P(H|R)P(L|R)P(F|R,H)。其中相应概率值可以查条件概率表。

由于上述例子只有一个未知随机变量，所以不用迭代。更一般的，使用贝叶斯网络进行推理的步骤可如下描述：

对所有可观察随机变量节点用观察值实例化；对不可观察节点实例化为随机值。
P(y|wi)=αP(y|Parents(y))∏jP(sj|Parents(sj))
对DAG进行遍历，对每一个不可观察节点y，计算，其中wi表示除y以外的其它所有节点，α为正规化因子，sj表示y的第j个子节点。
使用第三步计算出的各个y作为未知节点的新值进行实例化，重复第二步，直到结果充分收敛。
将收敛结果作为推断值。
以上只是贝叶斯网络推理的算法之一，另外还有其它算法，这里不再详述。

贝叶斯网络的构造、学习训练

构造与训练贝叶斯网络分为以下两步：
1、确定随机变量间的拓扑关系，形成DAG。这一步通常需要领域专家完成，而想要建立一个好的拓扑结构，通常需要不断迭代和改进才可以，需要用到机器学习得到。
2、训练贝叶斯网络。这一步也就是要完成条件概率表的构造，如果每个随机变量的值都是可以直接观察的，像我们上面的例子，那么这一步的训练是直观的，方法类似于朴素贝叶斯分类。但是通常贝叶斯网络的中存在隐藏变量节点，那么训练方法就是比较复杂，例如使用梯度下降法。

优化的贝叶斯网络结构要保证它产生的序列从头到尾的可能性最大，如果用概率做度量，就是后验概率最大。当然可以搜索所有可能的路径，但是会是一个NP-Hard问题。一般采用贪心算法，在每一步时沿着箭头方向寻找有限步，贪心容易陷入局部最优。为防止局部最优，采用蒙特卡洛方法，用许多随机数在贝叶斯网络中试试，看看是否陷入局部最优，但计算量较大。最近，新的方法是利用互信息，只保留互信息较大的节点的直接连接，然后再对简化的网络进行完备的搜索，找到全局优化的结构。

而节点之间弧的权重确定可以通过最大后验估计来得到，使用EM（expectation-maximization process）过程来解决。

一般的，参数和结构的交替训练的，先优化结构，再优化参数，然后再优化结构...直至得到收敛或者误差足够小的模型。

参考文献：

吴军《数学之美》
张洋《算法杂货铺——分类算法之贝叶斯网络(Bayesian networks)》

推荐阅读

（点击标题可跳转阅读）

李宏毅《机器学习》视频教程 PPT

一个算法工程师复现算法的踩坑总结

【机器学习】算法黑话大赏，我直呼好家伙！

【Python工具箱】自动可视化任何数据集！！！

Pycharm那些隐藏的实用小技巧，太强了

老铁，三连支持一下，好吗？↓↓↓