查找算法问什么?我和面试官进行了深入探讨…
关注、星标公众号,直达精彩内容
ID:技术让梦想更伟大
作者:李肖遥
线性查找介绍与实现
查找算法
从一些数据之中,找到一个特殊的数据,这种实现方法就是查找算法。它与遍历唯一的不同就是它并不一定会将每一个数据都进行访问,有些查找算法如二分查找等,并不需要完全访问所有的数据。
在我们的日常生活中,几乎每天都要进行一些查找的工作,比如在网盘的文件夹中查找某个文件,在微信中找到某人的联系方式,在已知次品商品的特征情况下,从一堆商品当中查找出这些次品等等。
算法简介
顺序查找算法是最简单的查找算法,其线性的从一个端点开始,将所有的数据依次访问,并求得所需要查找到的数据的位置。
代码实现
举个例子:有6个商品,他们每一个商品的重量都是10,但其中有一个商品是次品,他的重量只有9,其设计代码如下:
#include
int main(){
int i=0;
int commodity[6]={10,10,9,10,10,10};
for(i=0;i<6;i++){
if(commodity[i]==9){
printf("find it at :%d",i+1);
}
}
return 0;
}
折半查找(二分查找)介绍与实现
算法简介
二分查找也称折半查找,是一种效率较高的查找方法。折半查找要求线性表必须采用顺序存储结构,而且表中元素按关键字有序排列。
但有一种特殊情况可以不必须有序排列,即商品选取,从一堆标准重量为10的商品中查找出唯一的次品,这种特殊的数据情况也可以使用二分查找。
具体过程
二分查找是将n个元素分成大致相等的两部分,取a[n/2]与x做比较,如果x=a[n/2],则找到x,算法中止;
如果xx>a[n/2],则只要在数组a的右半部搜索x。
总共有n个元素,渐渐跟下去就是n,n/2,n/4,....n/2^k(接下来操作元素的剩余个数),其中k就是循环的次数。
由于n/2^k取整后>=1即令n/2^k=1可得k=log2n,所以时间复杂度为O(log2n)。
代码实现
//二分查找算法,找不到就返回-1,找到了就返回值
int binary_search(int * list,int len,int target) {
int low = 0;
int hight = len-1;
int middle;
while(low <= hight) {
middle = (low + hight)/2;
if(list[middle] = target) {
printf("已找到该值,数组下标为:%d\n",middle);
return list[middle];
} else if(list[middle] > target) {
hight = middle -1;
} else if(list[middle] < target) {
low = middle + 1;
}
}
printf("未找到该值");
return -1;
}
分块查找算法介绍与实现
算法简介
分块查找是折半查找和顺序查找的一种改进方法,由于分块查找只要求索引表是有序的,对块内节点没有排序要求,因此特别适合于节点动态变化的情况。
分块查找要求把一个大的线性表分解成若干块,每块中的节点可以任意存放,但块与块之间必须排序。
假设是按关键码值非递减的,那么对于任意的i,第i块中的所有节点的关键码值都必须小于第i+1块中的所有节点的关键码值。
此外,还要建立一个索引表,把每块中的最大关键码值作为索引表的关键码值,按块的顺序存放到一个辅助数组中,且按关键码值递减排序。
查找时,首先在索引表中进行查找,确定要找的节点所在的块,可以采用顺序查找或折半查找;然后,在相应的块中采用顺序查找,即可找到对应的节点。
具体过程
如图所示,假设要查找关键字 38 的具体位置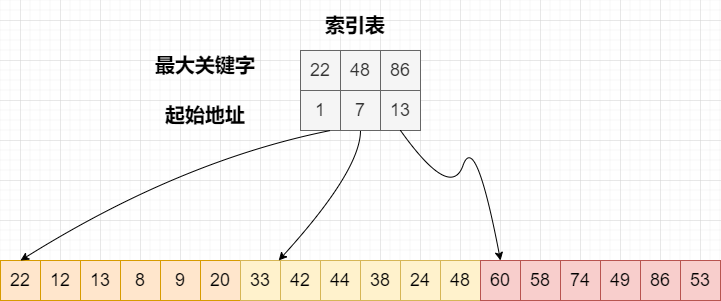
首先将 38 依次和索引表中各最大关键字进行比较,因为22 < 38 < 48,所以可以确定 38 如果存在,肯定在第二个子表中。
由于索引表中显示第二子表的起始位置在查找表的第 7 的位置上,所以从该位置开始进行顺序查找,一直查找到该子表最后一个关键字,找到即可。
代码实现
struct index
{
//定义块的结构
int key;
int start;
} newIndex[3]; //定义结构体数组
int search(int key, int a[])
{
int i, startValue;
i = 0;
while (i<3 && key>newIndex[i].key)
{
// 确定在哪个块中,遍历每个块,确定key在哪个块中
i++;
}
if (i>=3)
{
//大于分得的块数,则返回0
return -1;
}
startValue = newIndex[i].start; //startValue等于块范围的起始值
while (startValue <= startValue+5 && a[startValue]!=key)
{
startValue++;
}
if (startValue>startValue+5)
{
//如果大于块范围的结束值,则说明没有要查找的数
return -1;
}
return startValue;
}
动态查找-二叉排序树介绍与实现
算法简介
二叉排序树又称二叉查找树,亦称二叉搜索树。该树属于一种输入数据就默认产生一种顺序的数据结构。动态查找是一种输入时就会自动对其进行排序的数据结构。
算法性质
若左子树不空,则左子树上所有结点的值均小于或等于它的根结点的值;
若右子树不空,则右子树上所有结点的值均大于或等于它的根结点的值;
左、右子树也分别为二叉排序树;
查找实现
考虑如果树是空的,则查找结束,无匹配;如果被查找的值和根结点的值相等,查找成功。
如果被查找的值小于根结点的值就选择左子树,大于根结点的值就选择右子树。代码如下:
typedef int Status; /* Status是函数的类型,其值是函数结果状态代码,如OK等 */
/* 二叉树的二叉链表结点结构定义 */
typedef struct BiTNode /* 结点结构 */
{
int data; /* 结点数据 */
struct BiTNode *lchild, *rchild; /* 左右孩子指针 */
} BiTNode, *BiTree;
/* 递归查找二叉排序树T中是否存在key, */
/* 指针f指向T的双亲,其初始调用值为NULL */
/* 若查找成功,则指针p指向该数据元素结点,并返回TRUE */
/* 否则指针p指向查找路径上访问的最后一个结点并返回FALSE */
Status SearchBST(BiTree t, int key, BiTree f, BiTree *p)
{
if (!t) /* 查找不成功 */
{
*p = f;
return FALSE;
}
else if (key == t->data) /* 查找成功 */
{
*p = t;
return TRUE;
}
else if (key < t->data)
return SearchBST(t->lchild, key, t, p); /* 在左子树中继续查找 */
else
return SearchBST(t->rchild, key, t, p); /* 在右子树中继续查找 */
}
插入方法及实现
二叉排序的插入是建立在二叉排序的查找之上的,插入一个结点,就是通过查找发现该结点合适插入位置,把结点直接放进去。
若查找的关键字已经有在树中,则指向该数据结点,若查找的关键字没有在树中,则指向查找路径上最后一个结点。代码如下:
struct BiTree {
int data;
BiTree *lchild;
BiTree *rchild;
};
//在二叉排序树中插入查找关键字key
BiTree* InsertBST(BiTree *t,int key)
{
if (t == NULL)
{
t = new BiTree();
t->lchild = t->rchild = NULL;
t->data = key;
return t;
}
if (key < t->data)
t->lchild = InsertBST(t->lchild, key);
else
t->rchild = InsertBST(t->rchild, key);
return t;
}
//n个数据在数组d中,tree为二叉排序树根
BiTree* CreateBiTree(BiTree *tree, int d[], int n)
{
for (int i = 0; i < n; i++)
tree = InsertBST(tree, d[i]);
}
删除方法及实现
二叉树的删除会影响到树的其它部分的结构,删除的时候需要考虑以下几种情况:
删除结点为叶子结点;
删除的结点只有左子树;
删除的结点只有右子树
删除的结点既有左子树又有右子树。
参考代码如下:
/* 若二叉排序树T中存在关键字等于key的数据元素时,则删除该数据元素结点, */
/* 并返回TRUE;否则返回FALSE。 */
Status DeleteBST(BiTree *T,int key)
{
if(!*T) /* 不存在关键字等于key的数据元素 */
return FALSE;
else
{
if (key==(*T)->data) /* 找到关键字等于key的数据元素 */
return Delete(T);
else if (key<(*T)->data)
return DeleteBST(&(*T)->lchild,key);
else
return DeleteBST(&(*T)->rchild,key);
}
}
/* 从二叉排序树中删除结点p,并重接它的左或右子树。 */
Status Delete(BiTree *p)
{
BiTree q,s;
if((*p)->rchild==NULL) /* 右子树空则只需重接它的左子树(待删结点是叶子也走此分支) */
{
q=*p; *p=(*p)->lchild; free(q);
}
else if((*p)->lchild==NULL) /* 只需重接它的右子树 */
{
q=*p; *p=(*p)->rchild; free(q);
}
else /* 左右子树均不空 */
{
q=*p; s=(*p)->lchild;
while(s->rchild) /* 转左,然后向右到尽头(找待删结点的前驱) */
{
q=s;
s=s->rchild;
}
(*p)->data=s->data; /* s指向被删结点的直接前驱(将被删结点前驱的值取代被删结点的值) */
if(q!=*p)
q->rchild=s->lchild; /* 重接q的右子树 */
else
q->lchild=s->lchild; /* 重接q的左子树 */
free(s);
}
return TRUE;
}
动态查找-平衡二叉树
算法简介
它是一棵空树或它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树。
常用实现方法有红黑树、AVL、替罪羊树、Treap、伸展树等,我们以AVL树为例。
AVL树算法性质
它必须是一颗二叉查找树
它的左子树和右子树都是平衡二叉树,且左子树和右子树的深度之差的绝对值不超过1。
若将二叉树节点的平衡因子BF定义为该节点的左子树的深度减去它的右子树的深度,则平衡二叉树上所有节点的平衡因子只可能为-1,0,1.
只要二叉树上有一个节点的平衡因子的绝对值大于1,那么这颗平衡二叉树就失去了平衡。
AVL树具体过程
AVL树的构建过程是通过在一棵平衡二叉树中依次插入元素,若出现不平衡,则要根据新插入的结点与最低不平衡结点的位置关系进行相应的调整。
各个调整的方法分为LL型、RR型、LR型和RL型4种类型,以其中一种LR型调整为例说明,如图所示:
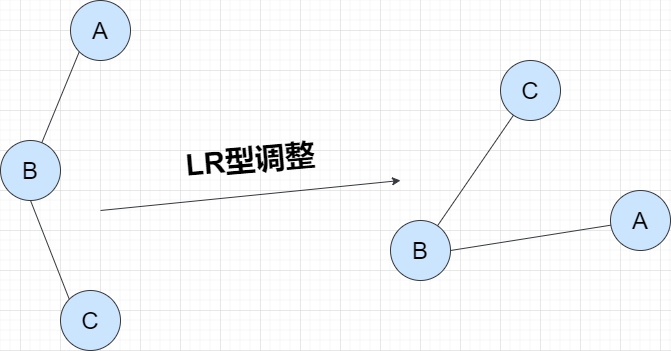
由于在A的左孩子(L)的右子树(R)上插入新结点,使原来平衡二叉树变得不平衡,此时A的平衡因子由1变为2。
按照大小关系,结点C应作为新的根结点,其余两个节点分别作为左右孩子节点才能平衡,操作如下:
将B的左孩子C提升为新的根结点
将原来的根结点A降为C的右孩子
各子树按大小关系连接(BL和AR不变,CL和CR分别调整为B的右子树和A的左子树)。
代码实现
//结点设计
typedef struct Node {
int key;
struct Node *left;
struct Node *right;
int height;
} BTNode;
int height(struct Node *N) {
if (N == NULL)
return 0;
return N->height;
}
int max(int a, int b) {
return (a > b) ? a : b;
}
BTNode* newNode(int key) {
struct Node* node = (BTNode*)malloc(sizeof(struct Node));
node->key = key;
node->left = NULL;
node->right = NULL;
node->height = 1;
return(node);
}
//ll型调整
BTNode* ll_rotate(BTNode* y) {
BTNode *x = y->left;
y->left = x->right;
x->right = y;
y->height = max(height(y->left), height(y->right)) + 1;
x->height = max(height(x->left), height(x->right)) + 1;
return x;
}
//rr型调整
BTNode* rr_rotate(BTNode* y) {
BTNode *x = y->right;
y->right = x->left;
x->left = y;
y->height = max(height(y->left), height(y->right)) + 1;
x->height = max(height(x->left), height(x->right)) + 1;
return x;
}
//判断平衡
int getBalance(BTNode* N) {
if (N == NULL)
return 0;
return height(N->left) - height(N->right);
}
//插入结点&数据
BTNode* insert(BTNode* node, int key) {
if (node == NULL)
return newNode(key);
if (key < node->key)
node->left = insert(node->left, key);
else if (key > node->key)
node->right = insert(node->right, key);
else
return node;
node->height = 1 + max(height(node->left), height(node->right));
int balance = getBalance(node);
if (balance > 1 && key < node->left->key) //LL型
return ll_rotate(node);
if (balance < -1 && key > node->right->key) //RR型
return rr_rotate(node);
if (balance > 1 && key > node->left->key) { //LR型
node->left = rr_rotate(node->left);
return ll_rotate(node);
}
if (balance < -1 && key < node->right->key) { //RL型
node->right = ll_rotate(node->right);
return rr_rotate(node);
}
return node;
}
//遍历
void preOrder(struct Node *root) {
if (root != NULL) {
printf("%d ", root->key);
preOrder(root->left);
preOrder(root->right);
}
}
总结
这里介绍了几种常见,项目中常用的代码,帮助大家了解,内容也比较基础,希望对大家有学习作用,我们下一期,再见!
嵌入式编程专辑 Linux 学习专辑 C/C++编程专辑 Qt进阶学习专辑 关注微信公众号『技术让梦想更伟大』,后台回复“m”查看更多内容。 长按前往图中包含的公众号关注
