作者Cat-shao，真名邵振轩，辽宁OIer，年仅12岁，非常感谢他的投稿。

Part 1 我学它干啥？

树状数组，Binary Indexed Tree（简称BIT），是由Peter M. Fenwick在1994年发明的
——百度百科

名字十分高大上，那么它是干什么的呢？

求和

求和是树状数组中的一个应用，并不是只能求和，本文使用求和作为例子。

现在有一个数组a，我们需要求很多次数组中不同区间的和，而且多次对a中随意一项进行更改。
比如说a = {0, 1, 5, 3, 2, 4}

第一次求[1, 3]，得到1 + 5 + 3 = 9
第二次求[2, 4]，得到5 + 3 + 2 = 10
第三次，这时候我把a[2] += 2
第四次求[1, 5]，得到1 + 7 + 3 + 2 + 4 = 17

[l, r]表示从下标l开始，到r结束的区间，包含l和r。
l: left
r: right

这时候很多同学想到的第一个方法，就是直接挨个加起来不就好了吗？

可此题暗藏玄机，我们要进行多次求和啊，每一次都重新计算太慢，能不能提前加好一些区域，反复使用呢？
这就要请出我们的主角了——树状数组

Part 2 lowbit

树状数组的结构十分精妙，其中离不开一个基本运算——lowbit

lowbit(i) 可以解释为：i中最低位的1以及后面的0；或者你可以把它理解成i能被n整除，n还可以写成2k

一种lowbit的实现方式为lowbit(x) = x & -x

long long lowbit(long long x) {
    return x & -x;
}

还是拿172举例子，化成二进制后我们发现除了尾部的100相同之外，其他位都不同，使用按位与能得到lowbit的值

Part 3 树状数组

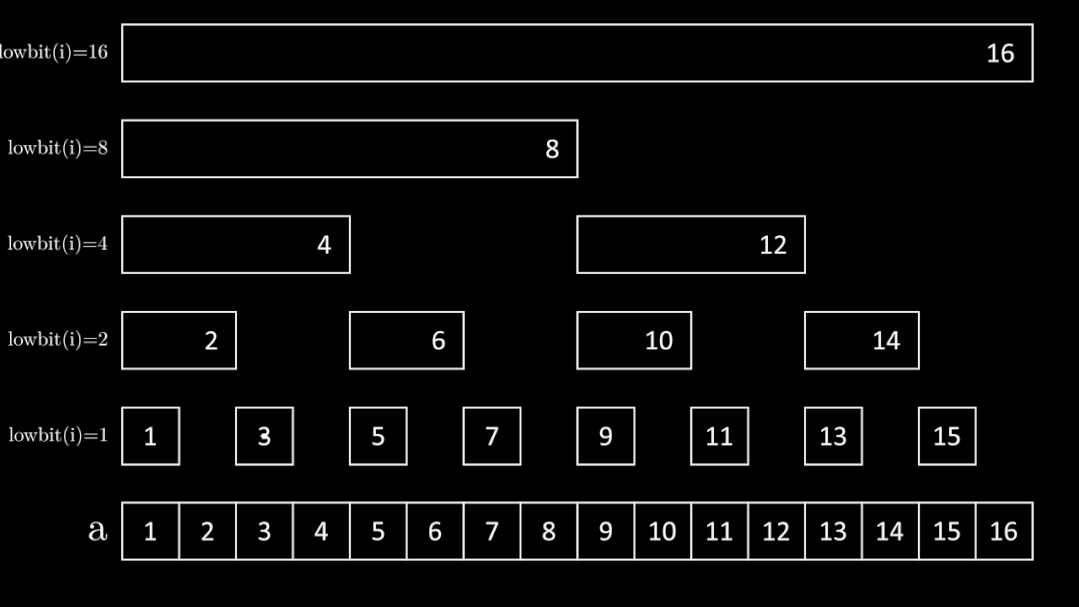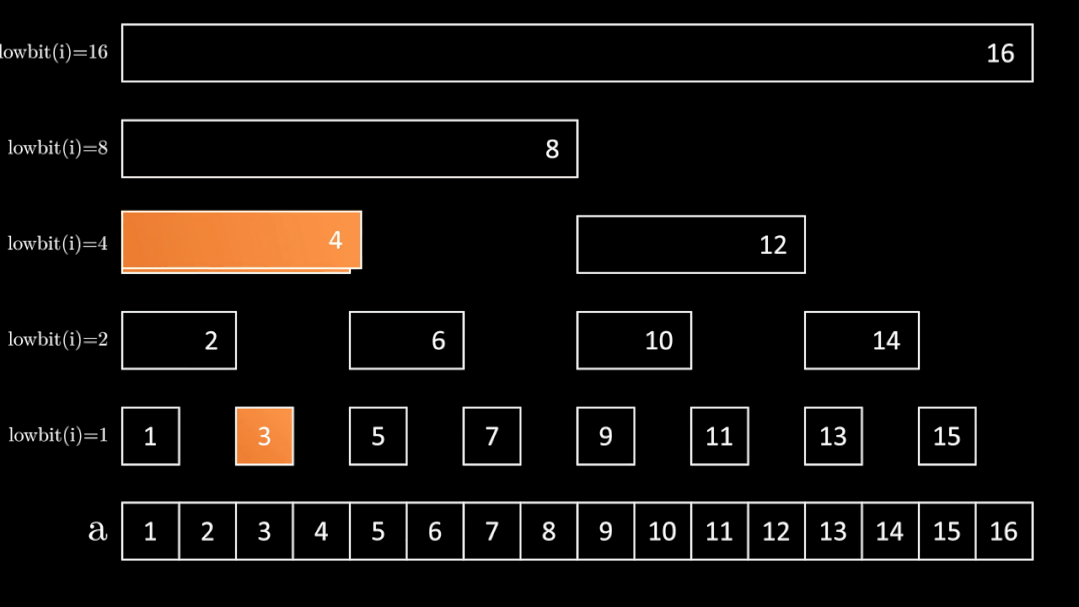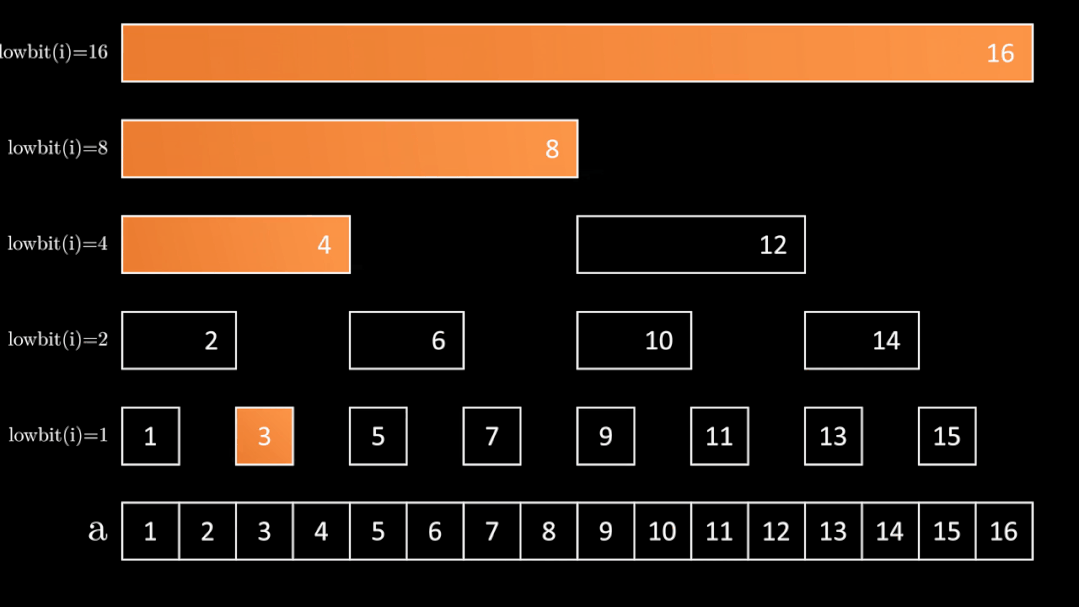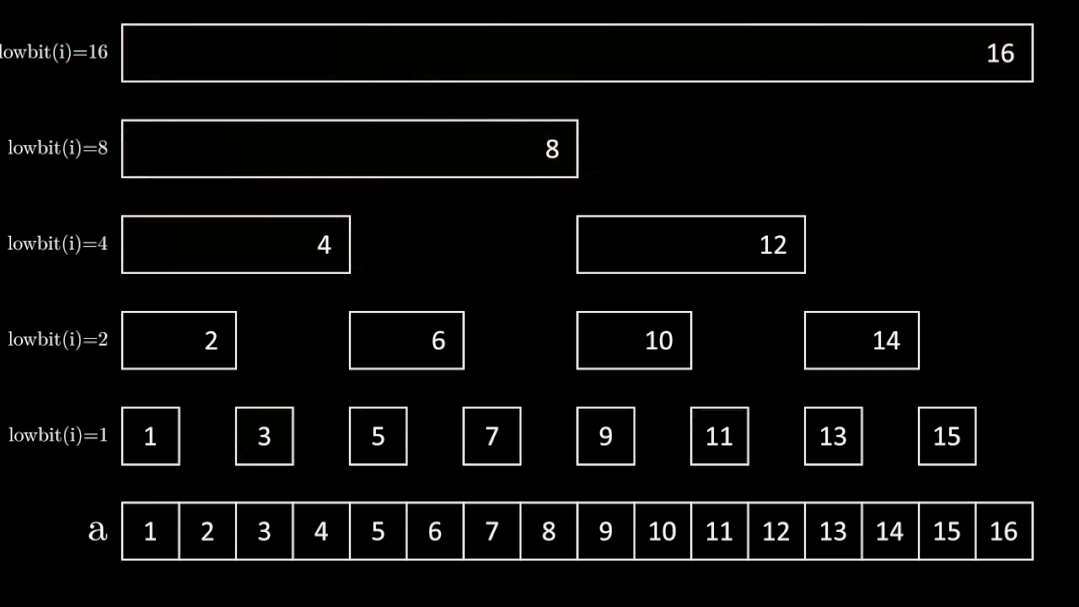
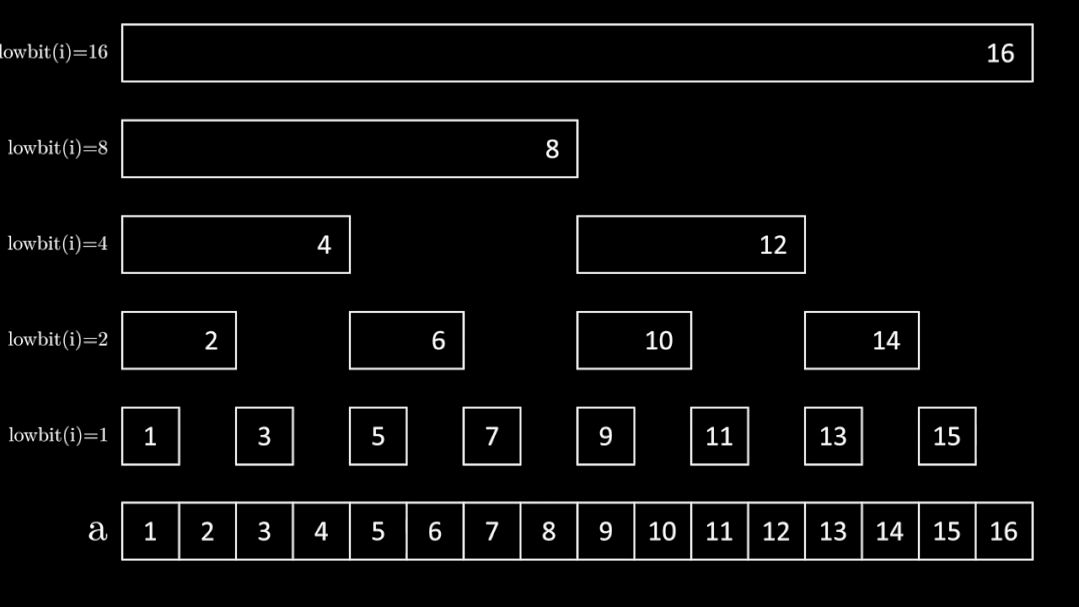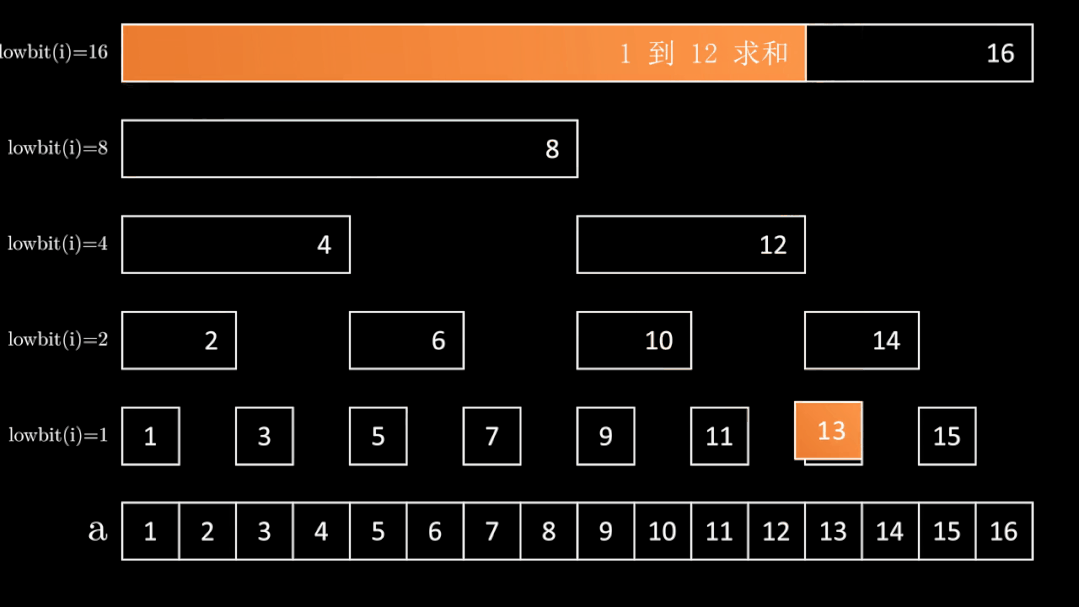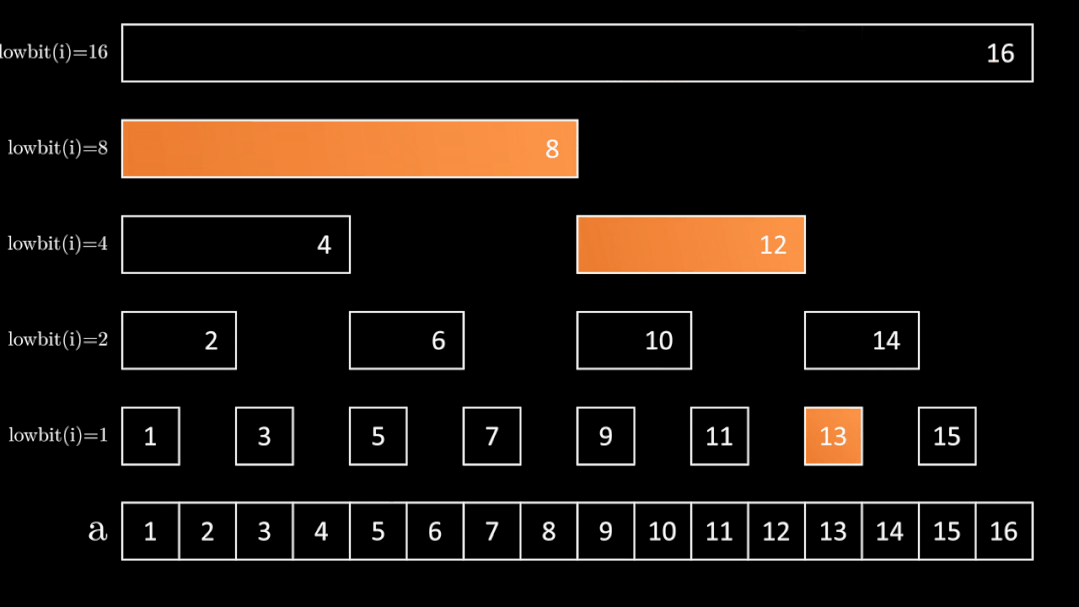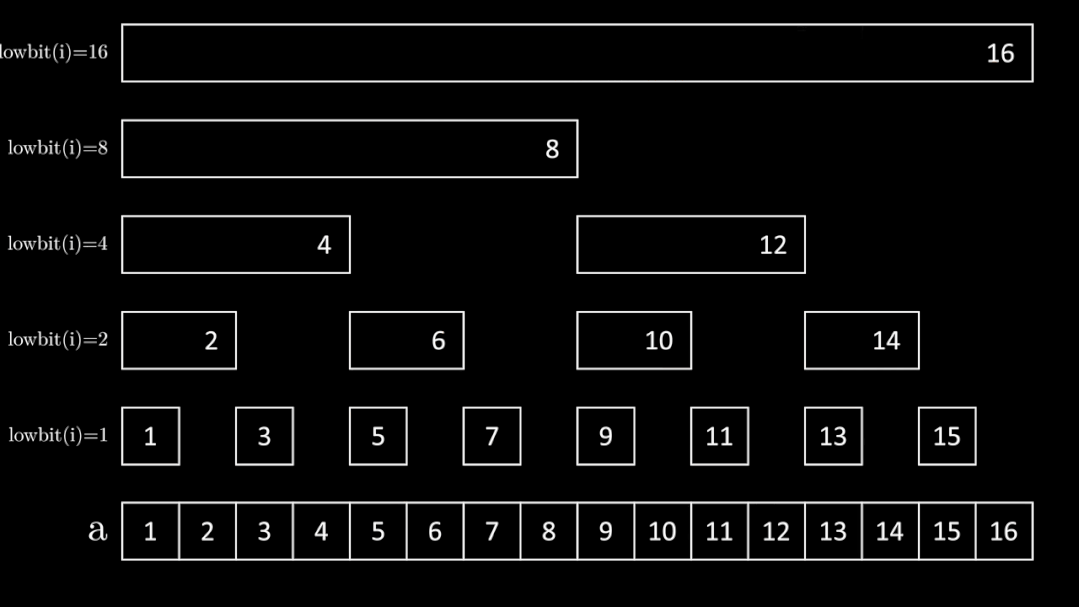
既然名字叫树状数组，那它必然是个数组，可外表下藏着二叉树的结构。
精巧的结构与lowbit密不可分，真是妙极了。

以下内容中，我们在这里管原始的数组叫做a，树状数组（经过处理）叫做bit，三个图中的数字均为下标，不是值！

结构

bit中存放了多个数的和，那么具体存了几个，在哪里呢？
我们规定，bit[i]中存从右往左数lowbit(i)个数。

bit[i] = 在数组a中从 i - lowbit(i) + 1 到 i 求和

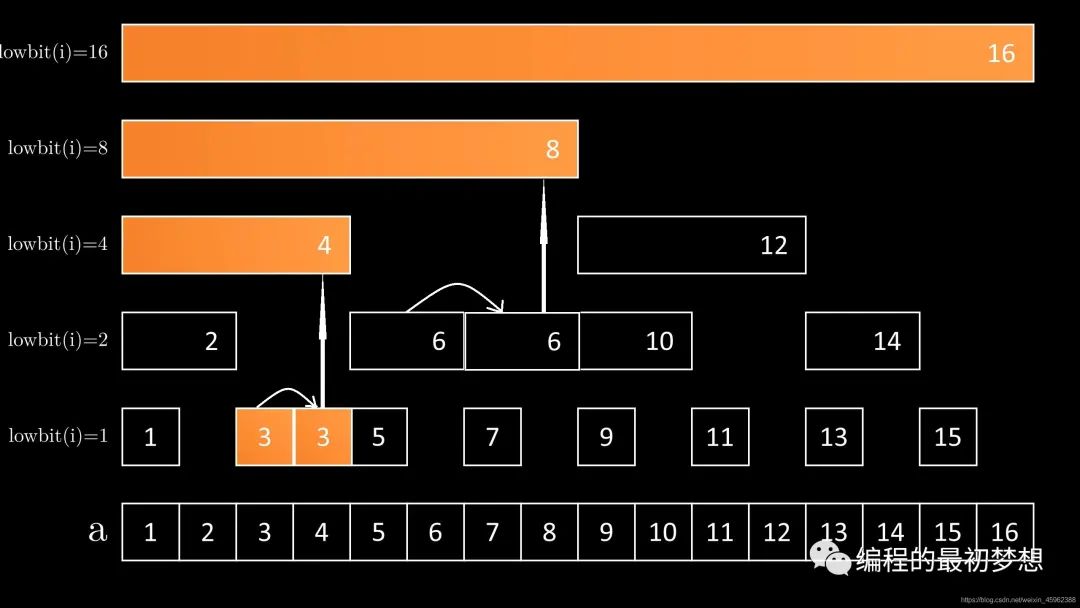
更改单个数值

首先，更改数据可以转换成加法，我们这里讨论加法，和更改是一样的。

挨个加起来时，更改a[i]只需要动它一个就可以了。
可是在树状数组中，可能有好几项，都包括这个a[i]。

拿a[3]来举例子吧。

bit[3] 对应 a的[3, 3] 的和
bit[4] 对应 a的[1, 4] 的和
bit[8] 对应 a的[1, 8] 的和
bit[16] 对应 a的[1, 16] 的和

以上四个bit中的值都需要更改

在图中，我们可以看出，4在3头上，8在4头上，16在8头上。我们只需要找到一种方式，得到一个块头上的块，然后使用循环能推出整串。

如何找到自己头上的数呢？

图中的6和橘色没关系，是第二组例子

我们发现，在当前块的位置加上当前块的长度之后能跳到头上。
我是这么理解的：加上一个当前块后会把局部的空缺补上，合并成了一块，而这块也许也补了更大的空缺，这样就一次跳了好几级

上文定义规定了第i个块长度 = lowbit(i)，拿来用即可。

c++实现：

void add(int index, long long value) {
    while (index <= n) { // 更新直到最大的块
        node[index] += value; // 更新当前的块
        index += lowbit(index); // 加上一个自己的长度，补上空缺，得到下一个块
    }
}

区间求和

先考虑[1, r]的求和
从右往左取块，将块代表的数值加起来即可

图中的例子：

第一次取到13，长度为lowbit(13) = 1
第二次13取完了从12开始取，长度为4，一次性将[9, 12]取完
第三次[9, 13]取完了从8开始，长度为8，取走[1, 8]，到此[1, 13]全部取走

c++实现

long long sum(int index) {
    long long sum = 0;
    while (index > 0) {
        sum += node[index];
        index -= lowbit(index);
    }
    return sum;
}

那如果求和左端点不在1处呢？

对[l, r]求和，可以写成sum(r) - sum(l - 1)
先把大区域[1, r]求出来，然后扣掉[1, l - 1]的部分，不就是[l, r]吗？

构造

以上的“幻想”只是存在于树已经有了之后，如何根据数组a（原始数组），来构造一棵树呢？
一个简单的方法：

把数组bit全初始化为0
遍历整个数组a
对于每一个数组a[i]，都对bit进行add(i, a[i])

每一次add之后都能保证树状数组是正确的，全加一遍后自然构建出一整棵树。

时间复杂度对比

下面的暴力指的是开头提到的挨个相加。

求和

暴力：O(n)（挨个相加，加n次）
树状数组：O(log n)（结构与二叉树相仿）

更改

暴力：O(1)（改一次即可）
树状数组：O(log n)（需要改一串，但结构与二叉树相仿）

构造

暴力：O(n)（当做是读入的复杂度）
树状数组：O(n log n)（做n次加法，每次加法为log n）

树状数组适合在：多次求和，多次修改，数据量大的场景下使用。

如果无需支持修改，建议使用前缀和，构造O(n)，求和O(1)

代码

下面给出的是C++代码。

BITMain为树状数组的使用案例，对应洛谷树状数组https://www.luogu.com.cn/problem/P3374。

//
// Created by Cat-shao on 2021/2/9.
//
#include <cstdio>
#include <cstring>
using namespace std;

const long long MAX_N = 5000100;

long long lowbit(long long x) {
    return x & -x;
}

class BIT {
public:
    long long node[MAX_N], n;

    BIT(int _n) {
        memset(node, 0, sizeof(node));
        n = _n;
    }

    long long sum(int index) {
        long long sum = 0;
        while (index > 0) {
            sum += node[index];
            index -= lowbit(index);
        }
        return sum;
    }

    void add(int index, long long value) {
        while (index <= n) {
            node[index] += value;
            index += lowbit(index);
        }
    }
};

int BITMain()
{
    // https://www.luogu.com.cn/problem/P3374
    int n, m, op, x, y;
    long long value;
    scanf("%d%d", &n, &m);
    BIT tree = BIT(n);
    for (int i = 1; i <= n; ++i) {
        scanf("%lld", &value);
        tree.add(i, value);
    }

    for (int i = 0; i < m; ++i) {
        scanf("%d%d%d", &op, &x, &y);
        if (op == 1) {
            tree.add(x, y);
        } else if (op == 2) {
            printf("%lld\n", (tree.sum(y) - tree.sum(x - 1)));
        }
    }
    return 0;
}

int main()
{
    BITMain();
}

参考：

胡凡《算法笔记》

如果你有什么疑惑，可以留下评论，谢谢。

什么是树状数组？让这个12岁年轻人为你讲解