C#刷剑指Offer | 斐波那契数列-技术圈

我们来用之前学到的数据结构知识来刷《剑指Offer》的一些核心题目（精选了其中30+道题目），希望对你有帮助！本文题目为：斐波那契数列。

画外音：后台回复剑指offer，即可获得pdf下载链接哟！

1题目介绍

题目：写一个函数，输入n，求斐波那契（Fibonacci）数列的第n项。斐波那契数列的定义如下：　

2解题思路

怎么样，有高效的解法吗？

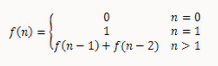
很多C/C++/C#/Java语言教科书在讲述递归函数的时候，大多都会用Fibonacci作为例子，因此我们会对这种解法烂熟于心：

public static long FibonacciRecursively(uint n){    if (n <= 0)    {        return 0;    }    if (n == 1)    {        return 1;    }
    return FibonacciRecursively(n - 1) + FibonacciRecursively(n - 2);}

上述递归的解法有很严重的效率问题，通过求解第10项的调用过程图来分析：

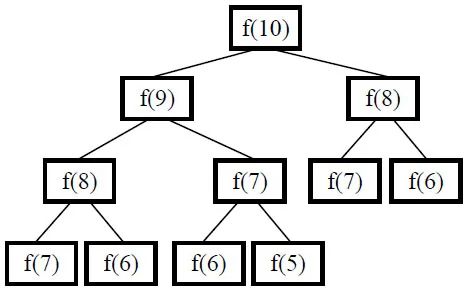
从上图中不难发现：在这棵树中有很多结点是重复的，而且重复的结点数会随着n的增大而急剧增加，这意味计算量会随着n的增大而急剧增大。事实上，用递归方法计算的时间复杂度是以n的指数的方式递增的。

改进的方法并不复杂。上述递归代码之所以慢是因为重复的计算太多，我们只要想办法避免重复计算就行了。这里的办法是从下往上计算，首先根据f(0)和f(1)算出f(2)，再根据f(1)和f(2)算出f(3)……依此类推就可以算出第n项了。很容易理解，这种思路的时间复杂度是O(n)。

3解决问题

代码实现

当然是用我们最熟悉的C#代码来实现一下：

public static long FibonacciIteratively(uint n){    int[] result = { 0, 1 };    if (n < 2)    {        return result[n];    }
    long fibNMinusOne = 1;    long fibNMinusTwo = 0;    long fibN = 0;
    for (uint i = 2; i <= n; i++)    {        fibN = fibNMinusOne + fibNMinusTwo;
        fibNMinusTwo = fibNMinusOne;        fibNMinusOne = fibN;    }
    return fibN;}

单元测试

代码实现之后，我们需要写一定的单元测试来验证我们的代码实现。

[TestMethod]public void FibonacciTest1(){    Assert.AreEqual(FibonaaciHelper.FibonacciIteratively(0),0);}
[TestMethod]public void FibonacciTest2(){    Assert.AreEqual(FibonaaciHelper.FibonacciIteratively(1), 1);}
[TestMethod]public void FibonacciTest3(){    Assert.AreEqual(FibonaaciHelper.FibonacciIteratively(2), 1);}
[TestMethod]public void FibonacciTest4(){    Assert.AreEqual(FibonaaciHelper.FibonacciIteratively(3), 2);}
[TestMethod]public void FibonacciTest5(){    Assert.AreEqual(FibonaaciHelper.FibonacciIteratively(4), 3);}
[TestMethod]public void FibonacciTest6(){    Assert.AreEqual(FibonaaciHelper.FibonacciIteratively(5), 5);}
[TestMethod]public void FibonacciTest7(){    Assert.AreEqual(FibonaaciHelper.FibonacciIteratively(6), 8);}
[TestMethod]public void FibonacciTest8(){    Assert.AreEqual(FibonaaciHelper.FibonacciIteratively(7), 13);}
[TestMethod]public void FibonacciTest9(){    Assert.AreEqual(FibonaaciHelper.FibonacciIteratively(8), 21);}
[TestMethod]public void FibonacciTest10(){    Assert.AreEqual(FibonaaciHelper.FibonacciIteratively(9), 34);}
[TestMethod]public void FibonacciTest11(){    Assert.AreEqual(FibonaaciHelper.FibonacciIteratively(10), 55);}
[TestMethod]public void FibonacciTest12(){    Assert.AreEqual(FibonaaciHelper.FibonacciIteratively(40), 102334155);

① 单元测试通过结果

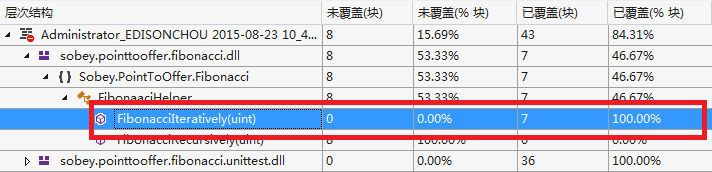
② 代码覆盖率

5参考资料

何海涛，《剑指Offer》

往期推荐

ASP.NET Core 学习手册

卧槽，超实用的Visual Studio插件

再见，PHP！

?点击获取文章源码