重温斐波那契数列,再看时间复杂度的重要性
• 开题引入斐波那契
• 代码演示:递归、循环
• 递归 vs 循环
• 时间复杂复高,指数型O(2^n);推导过程
• 占用线程堆栈, 可能导致栈满异常
• 压测演示
打入门软件开发,斐波那契数列便是绕不过去的简单编程算法。
一个老生常谈的思路是递归,另外是循环,今天借此机会回顾并演示时间复杂度在编程中的重要性。
斐波那契 递归算法 1,1,2,3,5,8,13,21,34,55
递归算法的应用场景是:
• 将大规模问题,拆解成几个小规模的同样问题
• 拆解具备终止场景
func Fibonacci(n int) (r int) {
if n == 1 || n == 2 {
r = 1
return
} else {
return Fibonacci(n-1) + Fibonacci(n-2)
}
}为什么能想到循环, 斐波那契数组也有循环的含义:
第n个数字是循环指针i从第1个数字移动到第n-2个数字时, 第n-2个数字pre和第n-1个数字next的和。
func Fibonacci2(n int) (r int) {
if n==1 || n==2 {
return 1
}
pre,next int :=1,1
for i:=0; i<=n-1-2; i++ {
tmp:= pre+next
pre = next
next = tmp
}
}单元测试如下:
func TestFibonacci(t *testing.T) {
t.Logf("Fibonacci(1) = %d, Fibonacci2(1)= %d ", Fibonacci(1), Fibonacci2(1))
t.Logf("Fibonacci(3) = %d, Fibonacci2(3)= %d ", Fibonacci(3), Fibonacci2(3))
t.Logf("Fibonacci(8) = %d, Fibonacci2(8)= %d ", Fibonacci(8), Fibonacci2(8))
}
go test ./ -v
=== RUN TestFibonacci
m_test.go:8: Fibonacci(1) = 1, Fibonacci2(1)= 1
m_test.go:9: Fibonacci(3) = 2, Fibonacci2(3)= 2
m_test.go:10: Fibonacci(8) = 21, Fibonacci2(8)= 21
--- PASS: TestFibonacci (0.00s)
PASS
ok example.github.com/test 3.359s递归的问题在于:
(1) 函数调用存在压栈过程,会在线程栈(一般2M)上留下栈帧,斐波那契递归算法:是函数自己调用自己,在终止条件后栈帧开始收敛,但是在此之前有可能已经撑爆线程栈。
栈帧中维持着函数调用所需要的各种信息,包括函数的入参、函数的局部变量、函数执行完成后下一步要执行的指令地址、寄存器信息等。
(2) 斐波那契递归调用存在重复计算,时间复杂度是O(2^n),随着n的增加,需要计算的次数陡然增大(业内称为指数型变化)。
f(n) = f(n-1)+f(n-2) // 1次计算
= f(n-2)+f(n-3)+f(n-3)+f(n-4) // 3次计算
= f(n-3)+f(n-4)+f(n-4)+f(n-5)+f(n-4)+f(n-5)+f(n-5)+f(n-6) // 7次计算 // 7次计算
=......
= f(1)+...... // 2^n-1次计算
故为斐波那契递归时间复杂度为 O(2^n) 而我们的循环算法不存在以上问题, 第n个数字需要n -2次计算, 时间复杂度是O(n)
有些童鞋可能没意识到指数型的威力,举个例子, 斐波那契递归算法,第20个数字需要2^20次运算;循环算法只要18次运算。
使用基准测试压测:
func BenchmarkF1(b *testing.B) {
for i := 1; i < b.N; i++ {
Fibonacci(20) // 时间复杂度 O(2^n)
}
}
func BenchmarkF2(b *testing.B) {
for i := 1; i < b.N; i++ {
Fibonacci2(20) // 时间复杂度 O(n)
}
}
go test -bench=. -benchmem ./
goos: darwin
goarch: amd64
pkg: example.github.com/test
cpu: Intel(R) Core(TM) i5-8257U CPU @ 1.40GHz
BenchmarkF1-8 55039 20740 ns/op 0 B/op 0 allocs/op
BenchmarkF2-8 196663548 6.080 ns/op 0 B/op 0 allocs/op
PASS
ok example.github.com/test 3.744s单次执行效率(ns/op指标)相形见绌,甚至斐波那契递归n>50+ 不一定能计算出来。
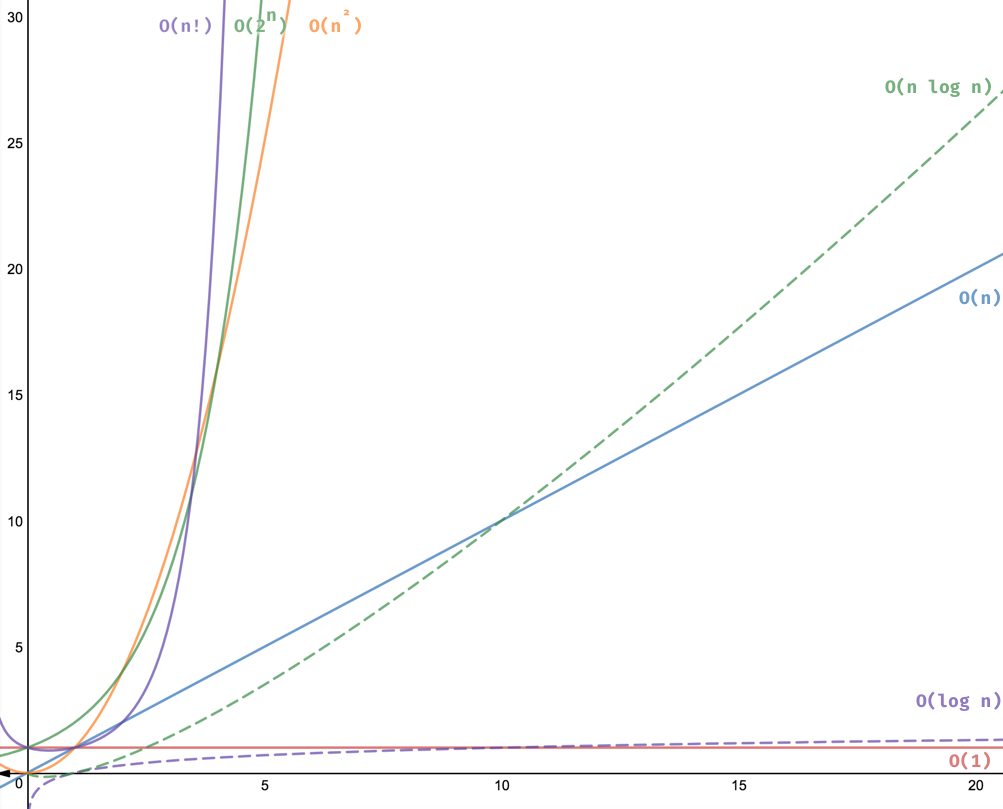
ok, that'all. 本次快速记录了递归算法相比循环的两点劣势,这里面很重要的常见时间复杂度变化曲线[1], 需要程序员必知必会。https://adrianmejia.com/most-popular-algorithms-time-complexity-every-programmer-should-know-free-online-tutorial-course/
全文原创,见字如面,若有不同见解或发散思维,文末可留言或直接微信喷我。
引用链接
[1] 常见时间复杂度变化曲线: https://adrianmejia.com/most-popular-algorithms-time-complexity-every-programmer-should-know-free-online-tutorial-course/

点“赞” 戳“在看”
戳“在看”
