在Graph领域，社区发现（Community detection）是一个非常热门且广泛的话题，后面会写一个系列，该问题实际上是从子图分割的问题演变而来，在真实的社交网络中，有些用户之间连接非常紧密，有些用户之间的连接较为稀疏，连接紧密的用户群体可以看做一个社区，在风控问题中，可以简单的理解为团伙挖掘。

目前的社区发现问题分为两大类：非重叠社区发现和重叠社区发现。非重叠社区发现问题描述的是：一个网络中，每个节点均只能属于同一个社区，这意味这社区和社区之间是没有交集的。在非重叠社区发现算法中，有不同种类的解法：

1）基于模块度的社区发现算法：基本思想是通过定义模块度（Modularity）来衡量一个社区的划分是不是相对比较好的结果，从而将社区发现问题转化为最大化模块度的问题进行求解，后续的Louvain算法会讲到。

2）基于标签传播的社区发现算法：基本思想是通过标记节点的标签信息来更新未标记节点的标签信息，在整个网络中进行传播，直至收敛，其中最具代表性的就是标签传播算法（LPA,Label Propagation Algorithm），也是本文要讨论的算法。

注意：在团伙挖掘的实际应用的过程中，不要寄希望于优化社区发现算法提高准确性，可能永远都解决不了问题，因为关系的形成在实际中太过于复杂，我们更多的关注构图关系的筛选、清洗、提纯，以及分群后进一步加工处理

一、LPA概述

Label Propagation Algorithm，也称作标签传播算法（LPA），是一个在图中快速发现社群的算法，由Raghavan等人在2007年于论文《Near linear time algorithm to detect community structures in large-scale networks》中提出。在 LPA 算法中，节点的标签完全由它的直接邻居决定。标签传播算法是一种基于标签传播的局部社区发现算法，其基本思想是节点的标签（community）依赖其邻居节点的标签信息，影响程度由节点相似度决定，并通过传播迭代更新达到稳定。

1、算法的思想

在用一个唯一的标签初始化每个节点之后，该算法会重复地将一个节点的标签社群化为该节点的相邻节点中出现频率最高的标签。当每个节点的标签在其相邻节点中出现得最频繁时，算法就会停止。该算法是异步的，因为每个节点都会在不等待其余节点更新的情况下进行更新。

该算法有5个步骤：

1）初始化网络中所有节点的标签，对于给定节点x，Cx(0)=x。

2）设置 t=1。

3）以随机顺序排列网络中的节点，并将其设置为x。

4）对于特定顺序选择的每个x∈X，让Cx(t)=f(Cxi1(t)，...，Cxim(t)，...。f这里返回相邻标签中出现频率最高的标签。如果有多个最高频率的标签，就随机选择一个标签。

5）如果每个节点都有其邻居节点中数量最多的标签，则停止算法，否则，设置t=t+1并转到3。

这是一个迭代的计算过程且不保证收敛，大体的思路就是每个人都看看自己的邻居都在什么社区内，看看频率最高的社区是啥，如果和自己当前的社区不一样，就把这个最高频社区当成是自己的社区，然后告诉邻居，周而复始，直到对于所有人，邻居们告诉自己的高频社区和自己当前的社区是一样的，算法结束。所以说对于这个算法，计算复杂度是O(kE)，k是迭代的次数，E是边的数量。大家的经验是这个迭代的次数大概是5次就能近似收敛，以实现精度和性能的平衡，能发现这个数字和六度分隔理论里面的数字也差不多。

我们可以很形象地理解算法的传播过程，当标签在紧密联系的区域，传播非常快，但到了稀疏连接的区域，传播速度就会下降。当出现一个节点属于多个社群时，算法会使用该节点邻居的标签与权重，决定最终的标签，传播结束后，拥有同样标签的节点被视为在同一群组中。

下图展示了算法的两个变种：Push 和 Pull。其中 Pull 算法更为典型，并且可以很好地并行计算：

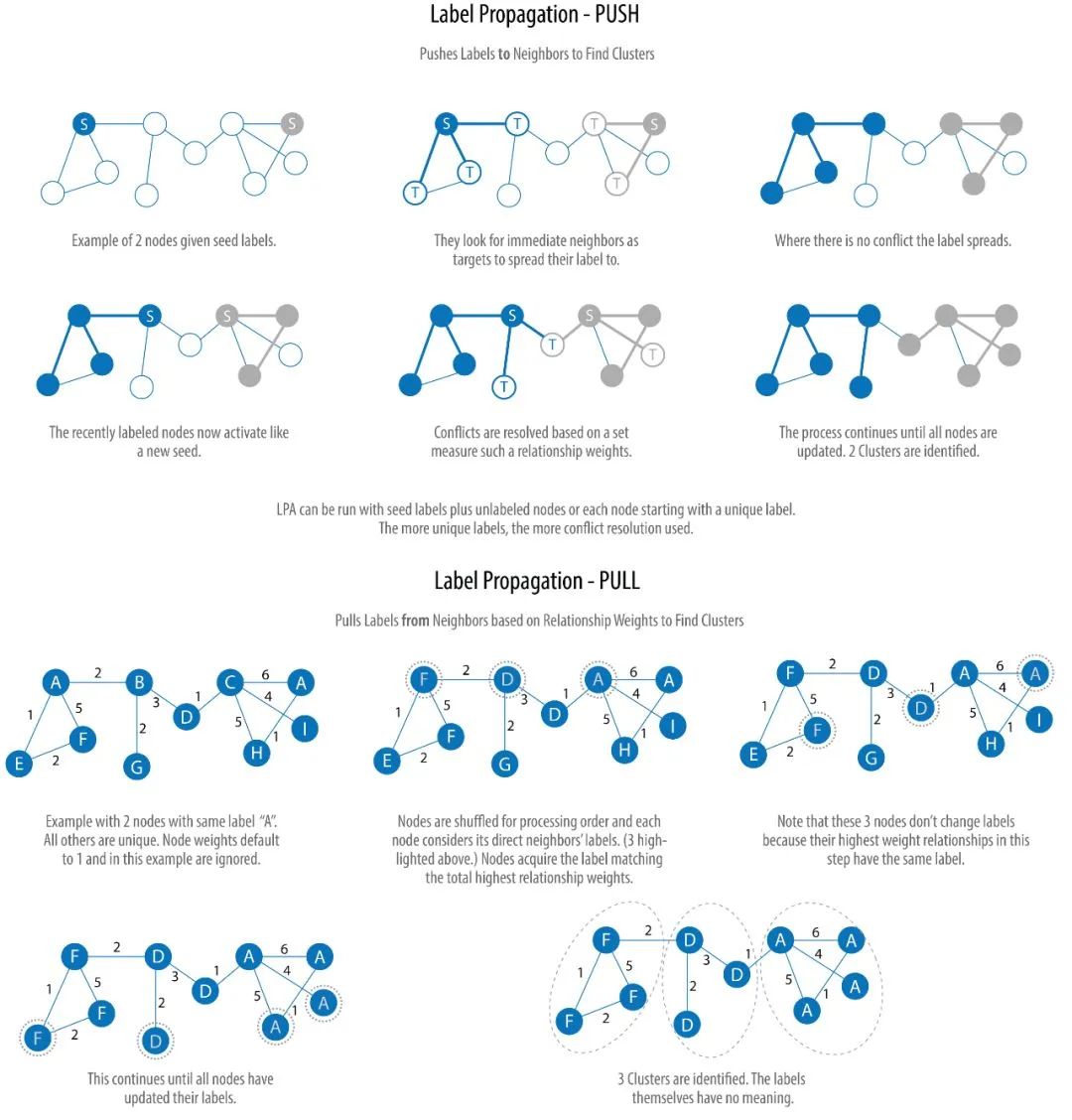
我们不再继续深入，看完上图，你应该已经理解了算法的大概过程。其实，做过图像处理的人很容易明白，所谓的标签传播算法，不过是图像分割算法的变种，Push 算法是区域生长法（Region Growing）的简化版，而 Pull 更像是分割和合并（divide-and-merge，也有人称 split-merge）算法。确实，图像（image）的像素和图（graph）的节点是十分类似的。

2、用于图聚类

图聚类是根据图的拓扑结构，进行子图的划分，使得子图内部节点的链接较多，子图之间的连接较少。依赖其邻居节点的标签信息，影响程度由节点相似度决定，并通过传播迭代更新达到稳定。

参考原始论文
https://arxiv.org/abs/0709.2938
https://arxiv.org/pdf/0709.2938.pdf

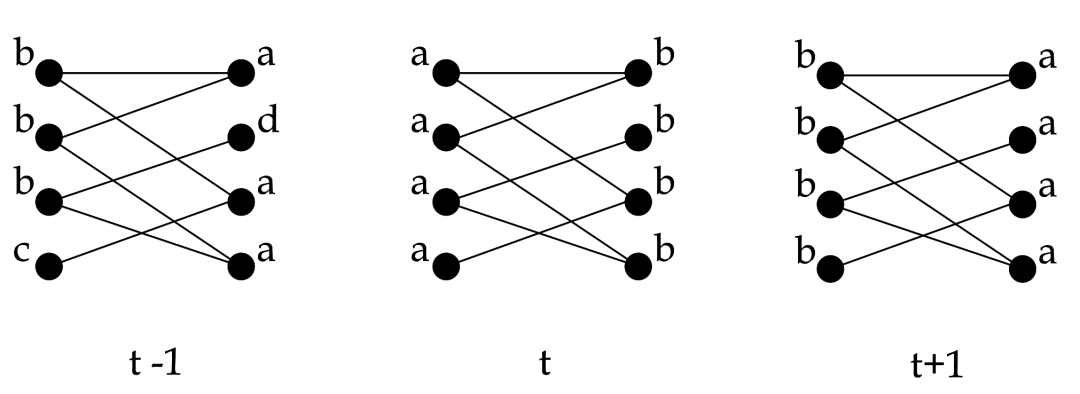
在算法开始之前为每个节点打上不同的标签，每一个轮次随机找到一个节点，查看其邻居节点的标签，找到出现次数最多的标签，随后将该节点改成该标签。当相邻两次迭代后社区数量不变或社区内节点数量不变时则停止迭代，下面看图解过程

初始化

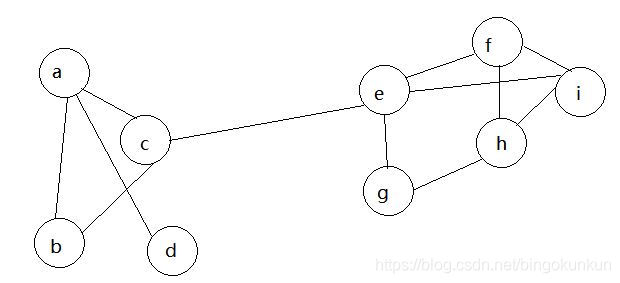
第一轮迭代

随机挑选一个节点（如c），发现其相邻节点有abe，三者出现次数相同，故随机选一个（如a），那么c点的标签被a替代。

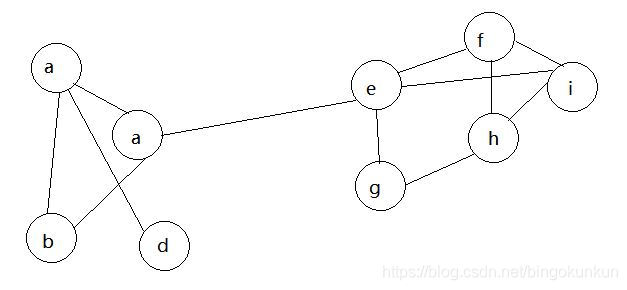
第二轮迭代

随机挑选一个节点（如b），发现其相邻节点均为a，故将b换成a，重复数次，最终的结果如图所示

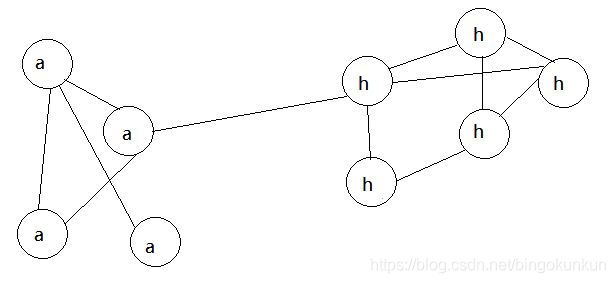
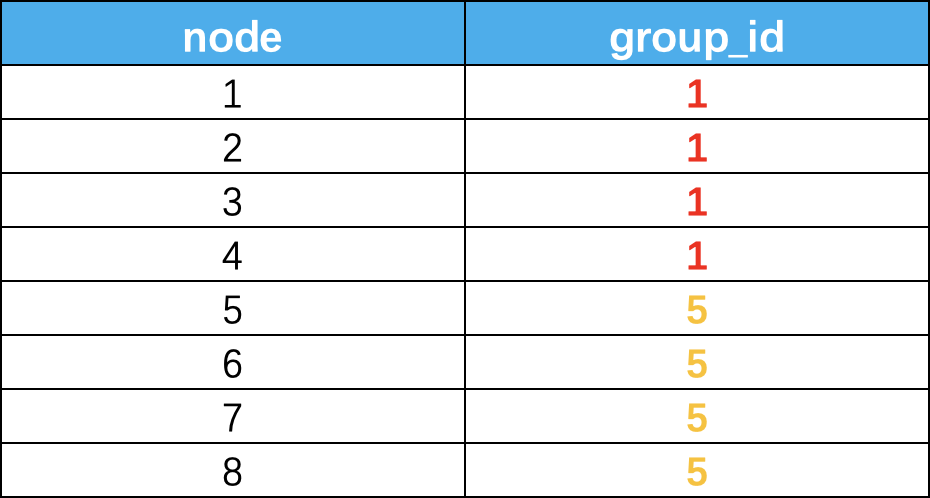
我们再看一个例子，比如下图：

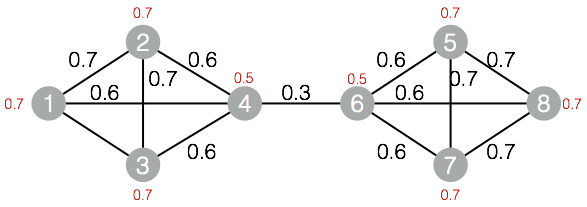
分组后的结果如下，我们得到了独立非重的groupid，这个结果其实是很难在实际场景中应用的，那么我们就的结果就没有意义了么？这个可以帮我们定位到浓度很高的群体，然后再加上部分属性标签，就能轻而易举的识别出问题黑产了。

3、用于半监督

该算法也可以作为半监督的分类算法，标签传播时一种半监督机器学习算法，它将标签分配给以前未标记的数据点。在算法开始时，数据点的子集（通常只占很小一部分）有标签（或分类）。在整个算法过程中，这些标签会传播到未标记的点。在标签传播过程中，保持已标注数据的标签不变，使其像一个源头把标签传向未标注数据。

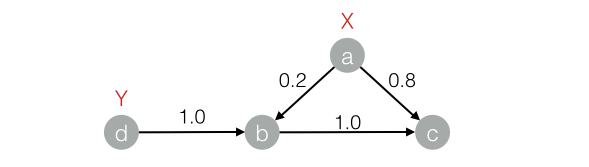
最终，当迭代过程结束时，相似节点的概率分布也趋于相似，可以划分到同一个类别中，从而完成标签传播过程，边的权重越大，表示两个节点越相似，那么label越容易传播过去。我们定义一个NxN的概率转移矩阵P：

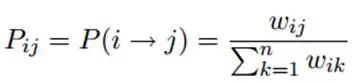
下面的图来看看传播过程

传播结束后的结果如下：

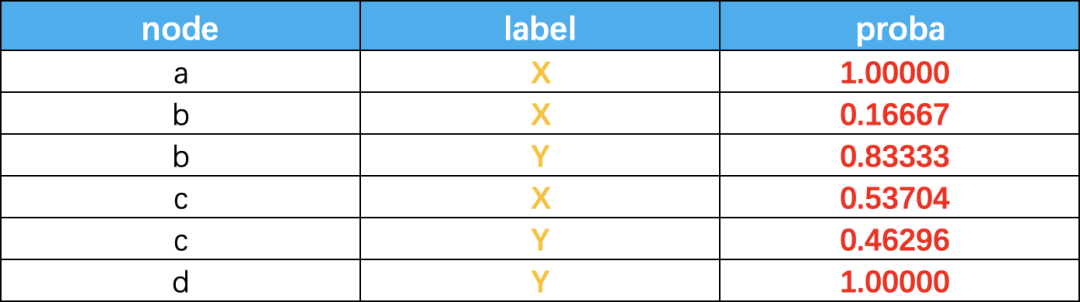
LPA使用已标记节点的标签作为基础，并尝试预测未标记节点的标签。然而，如果最初的标签是错误的，这可能会影响标签的传播过程，错误的标签可能会被传播。该算法是概率性的，并且发现的社区可能因执行的不同而不同。

二、算法代码实现

这个算法比较简单，有比较多的实现方式，最方便的还是networkx这个库，并用里面的一个简单的数据集进行试验。

1、数据集介绍

空手道数据集是一个比较简单的图数据集，下面我们看看其中的边和节点，后面应用这个数据集进行试验。

import networkx as nxG = nx.karate_club_graph() # 空手道G.nodes()NodeView((0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33))
G.edges() EdgeView([(0, 1), (0, 2), (0, 3), (0, 4), (0, 5), (0, 6), (0, 7), (0, 8),(0, 10), (0, 11), (0, 12), (0, 13), (0, 17), (0, 19), (0, 21), (0, 31), (1, 2), (1, 3), (1, 7), (1, 13), (1, 17), (1, 19), (1, 21), (1, 30), (2, 3), (2, 7), (2, 8), (2, 9), (2, 13), (2, 27), (2, 28), (2, 32), (3, 7), (3, 12), (3, 13), (4, 6), (4, 10), (5, 6), (5, 10), (5, 16), (6, 16), (8, 30), (8, 32), (8, 33), (9, 33), (13, 33), (14, 32), (14, 33), (15, 32), (15, 33), (18, 32), (18, 33), (19, 33), (20, 32), (20, 33), (22, 32), (22, 33), (23, 25), (23, 27), (23, 29), (23, 32), (23, 33), (24, 25), (24, 27), (24, 31), (25, 31), (26, 29), (26, 33),(27, 33), (28, 31), (28, 33), (29, 32), (29, 33), (30, 32), (30, 33),(31, 32), (31, 33), (32, 33)])

2、自己实现LPA算法

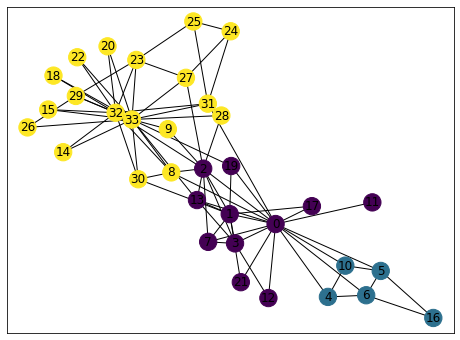
import randomimport networkx as nximport matplotlib.pyplot as plt    # 应该封装成类的形式  def lpa(G):      '''      异步更新方式      G：图      return：None      通过改变节点的标签，最后通过标签来划分社区      算法终止条件：迭代次数超过设定值      '''      max_iter_num = 0 # 迭代次数        while max_iter_num < 10:          max_iter_num += 1          print('迭代次数',max_iter_num)                for node in G:              count = {} # 记录邻居节点及其标签              for nbr in G.neighbors(node): # node的邻居节点                  label = G.nodes[nbr]['labels']                   count[label] = count.setdefault(label,0) + 1                            #找到出现次数最多的标签              count_items = sorted(count.items(),key=lambda x:-x[-1])              best_labels = [k for k,v in count_items if v == count_items[0][1]]              #当多个标签最大技术值相同时随机选取一个标签              label = random.sample(best_labels,1)[0] # 返回的是列表，所以需要[0]              G.nodes[node]['labels'] = label # 更新标签      def draw_picture(G):      # 画图      node_color = [float(G.nodes[v]['labels']) for v in G]      pos = nx.spring_layout(G) # 节点的布局为spring型      plt.figure(figsize = (8,6)) # 图片大小      nx.draw_networkx(G,pos=pos,node_color=node_color)      plt.show()    if __name__ == "__main__":      G = nx.karate_club_graph() #空手道数据集      # 给节点添加标签      for node in G:          G.add_node(node, labels = node) #用labels的状态      lpa(G)      com = set([G.nodes[node]['labels'] for node inG])      print('社区数量',len(com))      draw_picture(G)
迭代次数 1迭代次数 2迭代次数 3迭代次数 4迭代次数 5迭代次数 6迭代次数 7迭代次数 8迭代次数 9迭代次数 10社区数量 3

代码运行结果：

3、调包实现LPA算法

networkx集成了这个算法，可以直接调用

import matplotlib.pyplot as pltimport networkx as nxfrom networkx.algorithms.community import asyn_lpa_communities as lpa
# 空手道俱乐部G   = nx.karate_club_graph()com = list(lpa(G))print('社区数量',len(com))
com [{0, 1, 2, 3, 7, 8, 9, 11, 12, 13, 17, 19, 21, 30},{4, 5, 6, 10, 16},{14, 15, 18, 20, 22, 23, 24, 25, 26, 27, 28, 29, 31, 32, 33}]

# 下面是画图pos = nx.spring_layout(G) # 节点的布局为spring型NodeId    = list(G.nodes())node_size = [G.degree(i)**1.2*90 for i in NodeId] # 节点大小
plt.figure(figsize = (8,6)) # 设置图片大小nx.draw(G,pos,         with_labels=True,         node_size =node_size,         node_color='w',         node_shape = '.'       )
'''node_size表示节点大小node_color表示节点颜色with_labels=True表示节点是否带标签'''color_list = ['pink','orange','r','g','b','y','m','gray','black','c','brown']
for i in range(len(com)):    nx.draw_networkx_nodes(G, pos,                            nodelist=com[i],                            node_color = color_list[i+2],                             label=True)plt.show()

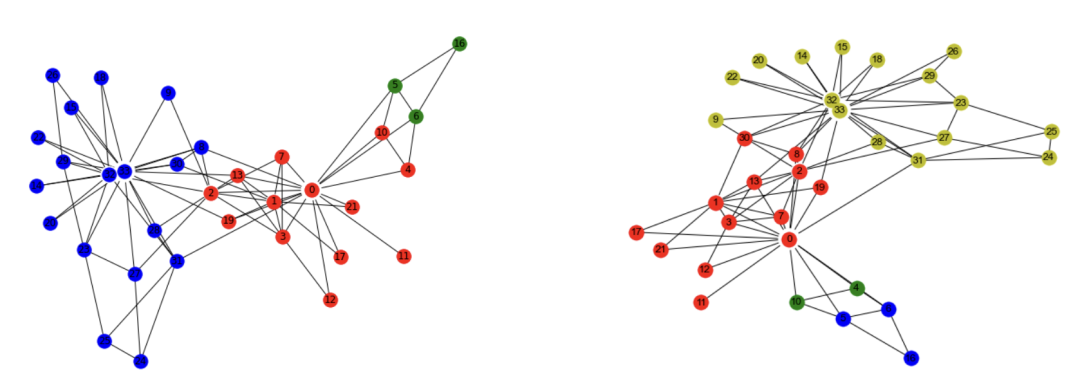
三、分群结果可视化

在可视化方面，确实R语言要强，大家有时间可以学习下，活儿全还是有点用处的，我们这里用R的igraph包来展现一些社区发现的结果。

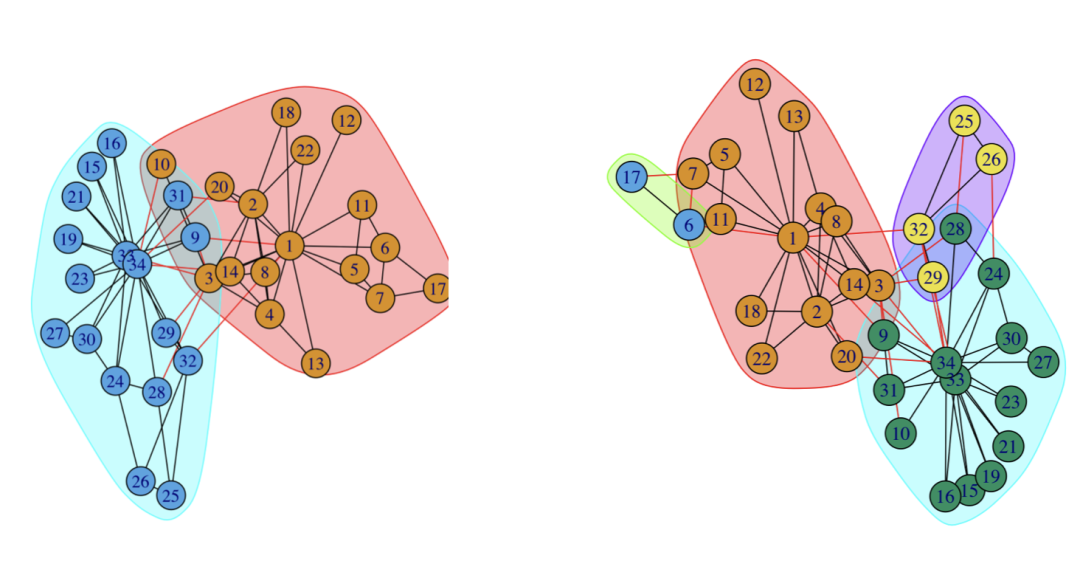
library('igraph')karate    <-  graph.famous("Zachary")community <- label.propagation.community(karate)# 计算模块度modularity(community)0.3717949
#membership查看每个点的各自分组情况。membership(community)1 1 1 1 1 1 1 1 2 1 1 1 1 1 2 2 1 1 2 1 2 1 2 2 2 2 2 2 2 2 2 2 2 2
plot(community,karate)

下面为两次跑的结果，可以看到，两次的结果并不一样，这个就是震荡效应导致的结果

换一个对比下看看

community <- walktrap.community(karate,                                weights = E(karate)$weight,                                 steps = 8,                                 merges =TRUE,                                 modularity = TRUE)plot(community,karate)

可以用更复杂的数据，画出来还挺好看的，数据集的下载地址：http://snap.stanford.edu/data/egonets-Facebook.html

library(igraph)library(d3Network)igraphDat <- read.graph(file = "/Users/wuzhengxiang/Documents/PPT模板/0.edges", directed = FALSE)
## Simplify to remove duplications and from-self-to-self loopsigraphDat <- simplify(igraphDat,              remove.multiple = TRUE,              remove.loops = TRUE             )
## Give numbersV(igraphDat)$label <- seq_along(V(igraphDat))
## Average path length between any two given nodes(averagePathLength <- average.path.length(igraphDat))
## Community structure detection based on edge betweennesscommunityEdgeBetwn <- edge.betweenness.community(igraphDat)
## Check the transitivity of a graph (probability that the adjacent vertices of a vertex are connected)(transitivityDat <- transitivity(igraphDat,              type = "localaverage",             isolates = "zero")             )
## Set the seed to get the same resultset.seed("20200513")
## Add community indicating background colorsplot(igraphDat,vertex.color = communityEdgeBetwn$membership, vertex.size = log(degree(igraphDat) + 1),mark.groups = by(seq_along(communityEdgeBetwn$membership), communityEdgeBetwn$membership, invisible)    )
## Annotatetitle("Stanford Facebook data",       sub = "http://snap.stanford.edu/data/egonets-Facebook.html"     )text(x = -1, y = -1,      labels = sprintf("Average path length: %.2f\nTransitivity: %.2f",                      averagePathLength,                       transitivityDat)    )

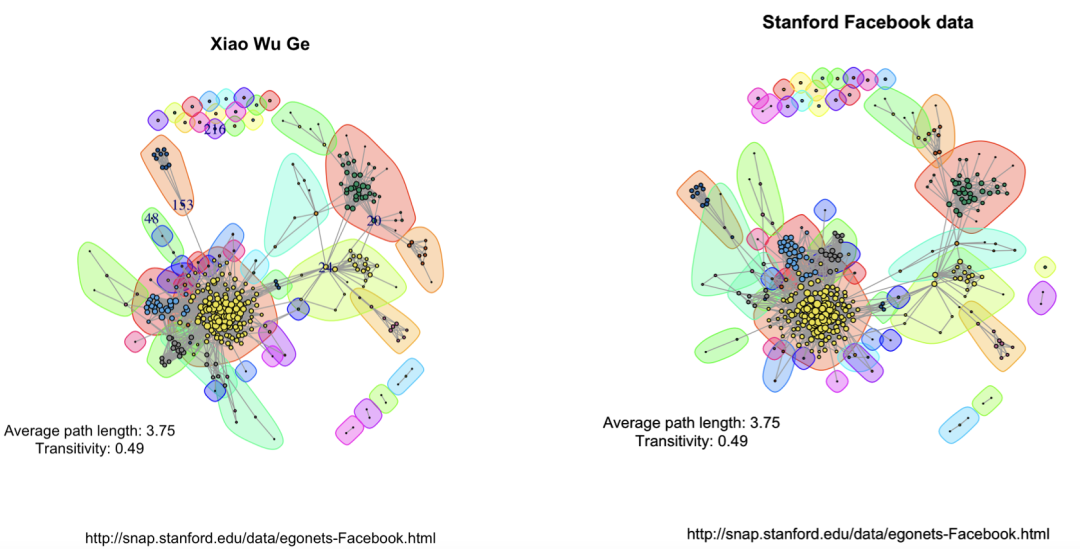
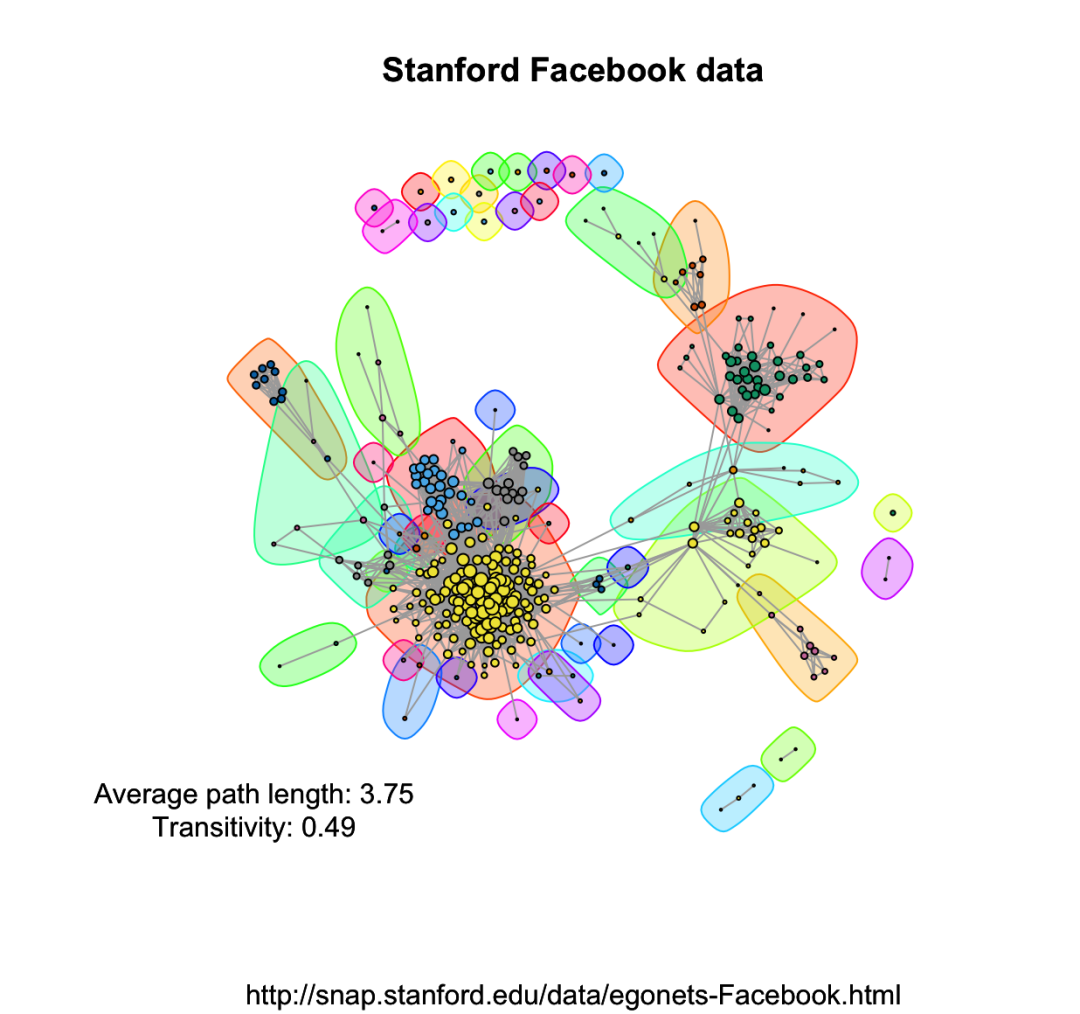
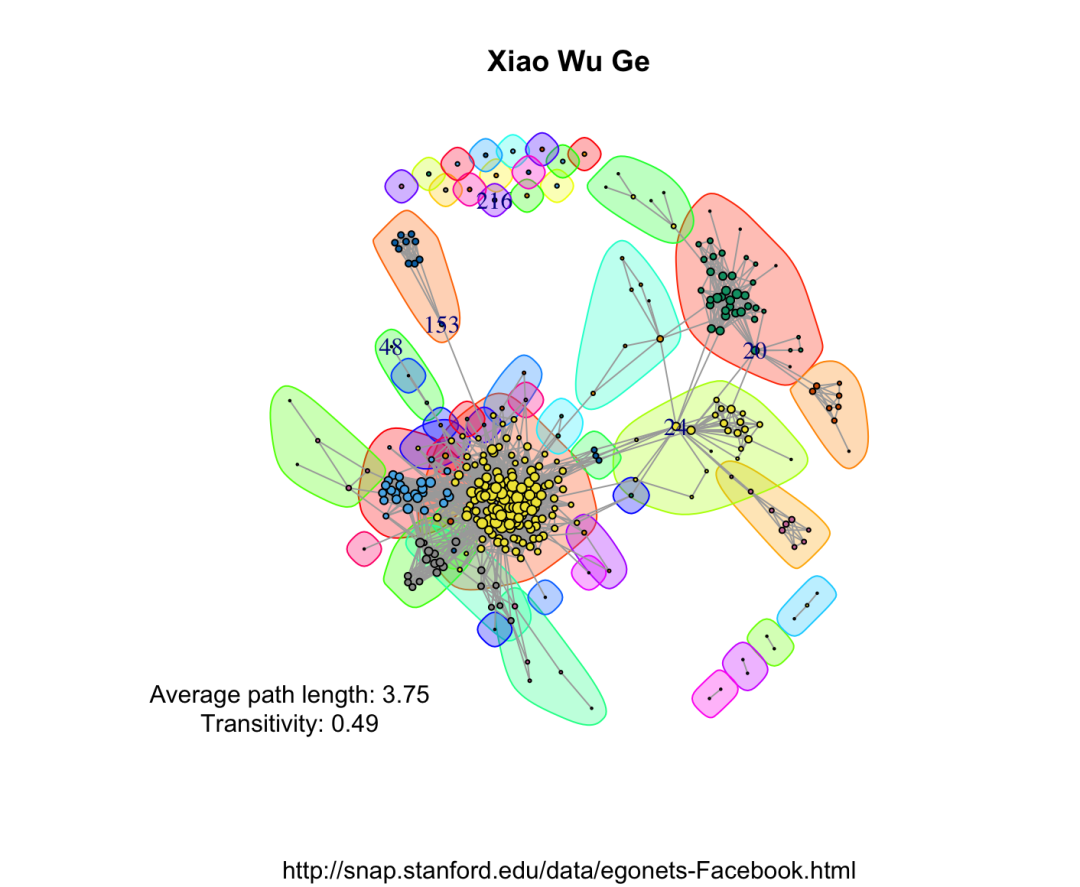
四、算法优缺点

作为一个比较简单的算法，其优缺点也是特别的明显。

1、算法优点

算法逻辑简单，时间复杂度低，接近线性复杂度，在超大规模网络下会有优异的性能，适合做社区发现的baseline。
无须定义优化函数，无须事先指定社区个数，算法会利用自身的网络结构来指导标签传播。

2、算法缺点

雪崩效应：社区结果不稳定，随机性强。由于当邻居节点的社区标签权重相同时，会随机取一个。导致传播初期一个小的错误被不断放大，最终没有得到合适的结果。尤其是异步更新时，更新顺序的不同也会导致最终社区划分结果不同。

上图中展示了一次标签传播算法的流程：初始化阶段，每个节点都以自己作为社区标签。比如a的社区就是a，c的社区就是c。当进入传播阶段，节点c的邻居节点共4个：a，b，c，d。而社区标签也是4个：a，b，c，d，假设随机取了一个a。

如果是异步更新，此时b，d，e三个节点的邻居节点中社区标签均存在2个a，所以他们都会立马更新成a。如果c当时随机选择的是b，那么d,e就会更新成b，从而导致b社区标签占优，而最终的社区划分也就成b了。

震荡效应：社区结果来回震荡，不收敛，当传播方式处于同步更新的时候，尤其对于二分图或子图存在二分图的结构而言，极易发生。

上图中展示了一次二分图中标签传播算法的流程，在同步更新的时候，每个节点依赖的都是上一轮迭代的社区标签。当二分图左边都是a，右边都是b时，a社区的节点此时邻居节点都是b，b社区的节点此时邻居节点都是a，根据更新规则，此时a社区的节点将全部更新为b，b社区的节点将全部更新为a。此时算法无法收敛，使得整个网络处于震荡中。

··· END ···


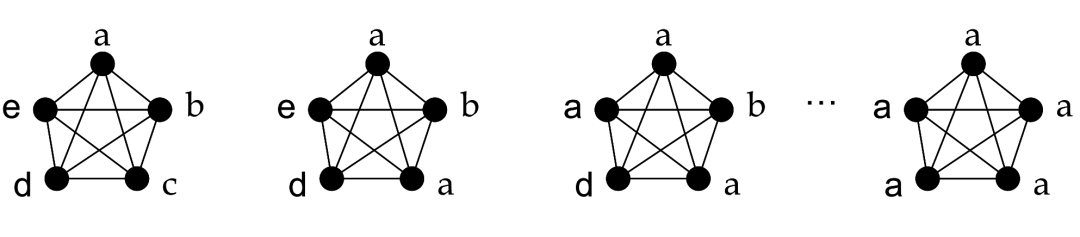
往期精彩回顾




适合初学者入门人工智能的路线及资料下载
(图文+视频)机器学习入门系列下载
中国大学慕课《机器学习》（黄海广主讲）
机器学习及深度学习笔记等资料打印
《统计学习方法》的代码复现专辑
机器学习交流qq群955171419，加入微信群请扫码：

社区发现之标签传播算法（LPA）