目标跟踪初探(DeepSORT)
点击上方“AI算法与图像处理”,选择加"星标"或“置顶”
重磅干货,第一时间送达
来源 | https://zhuanlan.zhihu.com/p/90835266,已授权转载,如需转载请联系原作者
简述
本文首先将介绍在目标跟踪任务中常用的匈牙利算法(Hungarian Algorithm)和卡尔曼滤波(Kalman Filter),然后介绍经典算法DeepSORT的工作流程以及对相关源码进行解析。
目前主流的目标跟踪算法都是基于Tracking-by-Detecton策略,即基于目标检测的结果来进行目标跟踪。DeepSORT运用的就是这个策略,上面的视频是DeepSORT对人群进行跟踪的结果,每个bbox左上角的数字是用来标识某个人的唯一ID号。
这里就有个问题,视频中不同时刻的同一个人,位置发生了变化,那么是如何关联上的呢?答案就是匈牙利算法和卡尔曼滤波。
匈牙利算法可以告诉我们当前帧的某个目标,是否与前一帧的某个目标相同。
卡尔曼滤波可以基于目标前一时刻的位置,来预测当前时刻的位置,并且可以比传感器(在目标跟踪中即目标检测器,比如Yolo等)更准确的估计目标的位置。
匈牙利算法(Hungarian Algorithm)
首先,先介绍一下什么是分配问题(Assignment Problem):假设有N个人和N个任务,每个任务可以任意分配给不同的人,已知每个人完成每个任务要花费的代价不尽相同,那么如何分配可以使得总的代价最小。
举个例子,假设现在有3个任务,要分别分配给3个人,每个人完成各个任务所需代价矩阵(cost matrix)如下所示(这个代价可以是金钱、时间等等):
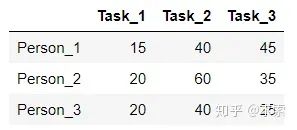
怎样才能找到一个最优分配,使得完成所有任务花费的代价最小呢?
匈牙利算法(又叫KM算法)就是用来解决分配问题的一种方法,它基于定理:
如果代价矩阵的某一行或某一列同时加上或减去某个数,则这个新的代价矩阵的最优分配仍然是原代价矩阵的最优分配。
算法步骤(假设矩阵为NxN方阵):
对于矩阵的每一行,减去其中最小的元素
对于矩阵的每一列,减去其中最小的元素
用最少的水平线或垂直线覆盖矩阵中所有的0
如果线的数量等于N,则找到了最优分配,算法结束,否则进入步骤5
找到没有被任何线覆盖的最小元素,每个没被线覆盖的行减去这个元素,每个被线覆盖的列加上这个元素,返回步骤3
继续拿上面的例子做演示:
step1 每一行最小的元素分别为15、20、20,减去得到:
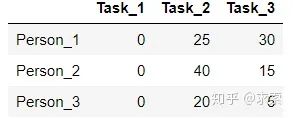
step2 每一列最小的元素分别为0、20、5,减去得到:

step3 用最少的水平线或垂直线覆盖所有的0,得到:

step4 线的数量为2,小于3,进入下一步;
step5 现在没被覆盖的最小元素是5,没被覆盖的行(第一和第二行)减去5,得到:
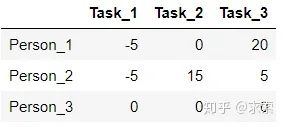
被覆盖的列(第一列)加上5,得到:

跳转到step3,用最少的水平线或垂直线覆盖所有的0,得到:
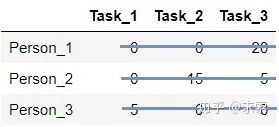
step4:线的数量为3,满足条件,算法结束。显然,将任务2分配给第1个人、任务1分配给第2个人、任务3分配给第3个人时,总的代价最小(0+0+0=0):
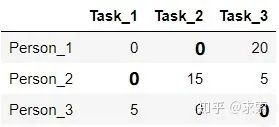
所以原矩阵的最小总代价为(40+20+25=85):
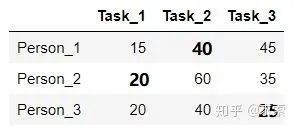
sklearn里的linear_assignment()函数以及scipy里的linear_sum_assignment()函数都实现了匈牙利算法,两者的返回值的形式不同:
import numpy as npfrom sklearn.utils.linear_assignment_ import linear_assignmentfrom scipy.optimize import linear_sum_assignmentcost_matrix = np.array([[15,40,45],[20,60,35],[20,40,25]])matches = linear_assignment(cost_matrix)print('sklearn API result:\n', matches)matches = linear_sum_assignment(cost_matrix)print('scipy API result:\n', matches)"""Outputssklearn API result:[[0 1][1 0][2 2]]scipy API result:(array([0, 1, 2], dtype=int64), array([1, 0, 2], dtype=int64))"""
在DeepSORT中,匈牙利算法用来将前一帧中的跟踪框tracks与当前帧中的检测框detections进行关联,通过外观信息(appearance information)和马氏距离(Mahalanobis distance),或者IOU来计算代价矩阵。
源码解读:
# linear_assignment.pydef min_cost_matching(distance_metric, max_distance, tracks, detections,track_indices=None, detection_indices=None):...# 计算代价矩阵cost_matrix = distance_metric(tracks, detections, track_indices, detection_indices)cost_matrix[cost_matrix > max_distance] = max_distance + 1e-5# 执行匈牙利算法,得到匹配成功的索引对,行索引为tracks的索引,列索引为detections的索引row_indices, col_indices = linear_assignment(cost_matrix)matches, unmatched_tracks, unmatched_detections = [], [], []# 找出未匹配的detectionsfor col, detection_idx in enumerate(detection_indices):if col not in col_indices:unmatched_detections.append(detection_idx)# 找出未匹配的tracksfor row, track_idx in enumerate(track_indices):if row not in row_indices:unmatched_tracks.append(track_idx)# 遍历匹配的(track, detection)索引对for row, col in zip(row_indices, col_indices):track_idx = track_indices[row]detection_idx = detection_indices[col]# 如果相应的cost大于阈值max_distance,也视为未匹配成功if cost_matrix[row, col] > max_distance:unmatched_tracks.append(track_idx)unmatched_detections.append(detection_idx)else:matches.append((track_idx, detection_idx))return matches, unmatched_tracks, unmatched_detections
卡尔曼滤波(Kalman Filter)
卡尔曼滤波被广泛应用于无人机、自动驾驶、卫星导航等领域,简单来说,其作用就是基于传感器的测量值来更新预测值,以达到更精确的估计。
假设我们要跟踪小车的位置变化,如下图所示,蓝色的分布是卡尔曼滤波预测值,棕色的分布是传感器的测量值,灰色的分布就是预测值基于测量值更新后的最优估计。

在目标跟踪中,需要估计track的以下两个状态:
均值(Mean):表示目标的位置信息,由bbox的中心坐标 (cx, cy),宽高比r,高h,以及各自的速度变化值组成,由8维向量表示为 x = [cx, cy, r, h, vx, vy, vr, vh],各个速度值初始化为0。
协方差(Covariance ):表示目标位置信息的不确定性,由8x8的对角矩阵表示,矩阵中数字越大则表明不确定性越大,可以以任意值初始化。
卡尔曼滤波分为两个阶段:(1) 预测track在下一时刻的位置,(2) 基于detection来更新预测的位置。
下面将介绍这两个阶段用到的计算公式。(这里不涉及公式的原理推导,因为我也不清楚原理(ಥ_ಥ) ,只是说明一下各个公式的作用)
预测
基于track在t-1时刻的状态来预测其在t时刻的状态。


在公式1中,x为track在t-1时刻的均值,F称为状态转移矩阵,该公式预测t时刻的x':

矩阵F中的dt是当前帧和前一帧之间的差,将等号右边的矩阵乘法展开,可以得到cx'=cx+dt*vx,cy'=cy+dt*vy...,所以这里的卡尔曼滤波是一个匀速模型(Constant Velocity Model)。
在公式2中,P为track在t-1时刻的协方差,Q为系统的噪声矩阵,代表整个系统的可靠程度,一般初始化为很小的值,该公式预测t时刻的P'。
源码解读:
# kalman_filter.pydef predict(self, mean, covariance):"""Run Kalman filter prediction step.Parameters----------mean: ndarray, the 8 dimensional mean vector of the object state at the previous time step.covariance: ndarray, the 8x8 dimensional covariance matrix of the object state at the previous time step.Returns-------(ndarray, ndarray), the mean vector and covariance matrix of the predicted state.Unobserved velocities are initialized to 0 mean."""std_pos = [self._std_weight_position * mean[3],self._std_weight_position * mean[3],1e-2,self._std_weight_position * mean[3]]std_vel = [self._std_weight_velocity * mean[3],self._std_weight_velocity * mean[3],1e-5,self._std_weight_velocity * mean[3]]motion_cov = np.diag(np.square(np.r_[std_pos, std_vel])) # 初始化噪声矩阵Qmean = np.dot(self._motion_mat, mean) # x' = Fxcovariance = np.linalg.multi_dot((self._motion_mat, covariance, self._motion_mat.T)) + motion_cov # P' = FPF(T) + Qreturn mean, covariance
更新
基于t时刻检测到的detection,校正与其关联的track的状态,得到一个更精确的结果。





在公式3中,z为detection的均值向量,不包含速度变化值,即z=[cx, cy, r, h],H称为测量矩阵,它将track的均值向量x'映射到检测空间,该公式计算detection和track的均值误差;
在公式4中,R为检测器的噪声矩阵,它是一个4x4的对角矩阵,对角线上的值分别为中心点两个坐标以及宽高的噪声,以任意值初始化,一般设置宽高的噪声大于中心点的噪声,该公式先将协方差矩阵P'映射到检测空间,然后再加上噪声矩阵R;
公式5计算卡尔曼增益K,卡尔曼增益用于估计误差的重要程度;
公式6和公式7得到更新后的均值向量x和协方差矩阵P。
源码解读:
# kalman_filter.py
def project(self, mean, covariance):
"""Project state distribution to measurement space.
Parameters
----------
mean: ndarray, the state's mean vector (8 dimensional array).
covariance: ndarray, the state's covariance matrix (8x8 dimensional).
Returns
-------
(ndarray, ndarray), the projected mean and covariance matrix of the given state estimate.
"""
std = [self._std_weight_position * mean[3],
self._std_weight_position * mean[3],
1e-1,
self._std_weight_position * mean[3]]
innovation_cov = np.diag(np.square(std)) # 初始化噪声矩阵R
mean = np.dot(self._update_mat, mean) # 将均值向量映射到检测空间,即Hx'
covariance = np.linalg.multi_dot((
self._update_mat, covariance, self._update_mat.T)) # 将协方差矩阵映射到检测空间,即HP'H^T
return mean, covariance + innovation_cov
def update(self, mean, covariance, measurement):
"""Run Kalman filter correction step.
Parameters
----------
mean: ndarra, the predicted state's mean vector (8 dimensional).
covariance: ndarray, the state's covariance matrix (8x8 dimensional).
measurement: ndarray, the 4 dimensional measurement vector (x, y, a, h), where (x, y) is the
center position, a the aspect ratio, and h the height of the bounding box.
Returns
-------
(ndarray, ndarray), the measurement-corrected state distribution.
"""
# 将mean和covariance映射到检测空间,得到Hx'和S
projected_mean, projected_cov = self.project(mean, covariance)
# 矩阵分解(这一步没看懂)
chol_factor, lower = scipy.linalg.cho_factor(projected_cov, lower=True, check_finite=False)
# 计算卡尔曼增益K(这一步没看明白是如何对应上公式5的,求线代大佬指教)
kalman_gain = scipy.linalg.cho_solve(
(chol_factor, lower), np.dot(covariance, self._update_mat.T).T,
check_finite=False).T
# z - Hx'
innovation = measurement - projected_mean
# x = x' + Ky
new_mean = mean + np.dot(innovation, kalman_gain.T)
# P = (I - KH)P'
new_covariance = covariance - np.linalg.multi_dot((kalman_gain, projected_cov, kalman_gain.T))
return new_mean, new_covariance
DeepSort工作流程
DeepSORT对每一帧的处理流程如下:
检测器得到bbox → 生成detections → 卡尔曼滤波预测→ 使用匈牙利算法将预测后的tracks和当前帧中的detecions进行匹配(级联匹配和IOU匹配) → 卡尔曼滤波更新
Frame 0:检测器检测到了3个detections,当前没有任何tracks,将这3个detections初始化为tracks
Frame 1:检测器又检测到了3个detections,对于Frame 0中的tracks,先进行预测得到新的tracks,然后使用匈牙利算法将新的tracks与detections进行匹配,得到(track, detection)匹配对,最后用每对中的detection更新对应的track
检测
使用Yolo作为检测器,检测当前帧中的bbox:
# demo_yolo3_deepsort.pydef detect(self):while self.vdo.grab():...bbox_xcycwh, cls_conf, cls_ids = self.yolo3(im) # 检测到的bbox[cx,cy,w,h],置信度,类别idif bbox_xcycwh is not None:# 筛选出人的类别mask = cls_ids == 0bbox_xcycwh = bbox_xcycwh[mask]bbox_xcycwh[:, 3:] *= 1.2cls_conf = cls_conf[mask]...
生成detections
将检测到的bbox转换成detections:
# deep_sort.pydef update(self, bbox_xywh, confidences, ori_img):self.height, self.width = ori_img.shape[:2]# 提取每个bbox的featurefeatures = self._get_features(bbox_xywh, ori_img)# [cx,cy,w,h] -> [x1,y1,w,h]bbox_tlwh = self._xywh_to_tlwh(bbox_xywh)# 过滤掉置信度小于self.min_confidence的bbox,生成detectionsdetections = [Detection(bbox_tlwh[i], conf, features[i]) for i,conf in enumerate(confidences) if conf > self.min_confidence]# NMS (这里self.nms_max_overlap的值为1,即保留了所有的detections)boxes = np.array([d.tlwh for d in detections])scores = np.array([d.confidence for d in detections])indices = non_max_suppression(boxes, self.nms_max_overlap, scores)detections = [detections[i] for i in indices]...
卡尔曼滤波预测阶段
使用卡尔曼滤波预测前一帧中的tracks在当前帧的状态:
# track.pydef predict(self, kf):"""Propagate the state distribution to the current time step using aKalman filter prediction step.Parameters----------kf: The Kalman filter."""self.mean, self.covariance = kf.predict(self.mean, self.covariance) # 预测self.age += 1 # 该track自出现以来的总帧数加1self.time_since_update += 1 # 该track自最近一次更新以来的总帧数加1
匹配
首先对基于外观信息的马氏距离计算tracks和detections的代价矩阵,然后相继进行级联匹配和IOU匹配,最后得到当前帧的所有匹配对、未匹配的tracks以及未匹配的detections:
# tracker.pydef _match(self, detections):def gated_metric(racks, dets, track_indices, detection_indices):"""基于外观信息和马氏距离,计算卡尔曼滤波预测的tracks和当前时刻检测到的detections的代价矩阵"""features = np.array([dets[i].feature for i in detection_indices])targets = np.array([tracks[i].track_id for i in track_indices]# 基于外观信息,计算tracks和detections的余弦距离代价矩阵cost_matrix = self.metric.distance(features, targets)# 基于马氏距离,过滤掉代价矩阵中一些不合适的项 (将其设置为一个较大的值)cost_matrix = linear_assignment.gate_cost_matrix(self.kf, cost_matrix, tracks,dets, track_indices, detection_indices)return cost_matrix# 区分开confirmed tracks和unconfirmed tracksconfirmed_tracks = [i for i, t in enumerate(self.tracks) if t.is_confirmed()]unconfirmed_tracks = [i for i, t in enumerate(self.tracks) if not t.is_confirmed()]# 对confirmd tracks进行级联匹配matches_a, unmatched_tracks_a, unmatched_detections = \linear_assignment.matching_cascade(gated_metric, self.metric.matching_threshold, self.max_age,self.tracks, detections, confirmed_tracks)# 对级联匹配中未匹配的tracks和unconfirmed tracks中time_since_update为1的tracks进行IOU匹配iou_track_candidates = unconfirmed_tracks + [k for k in unmatched_tracks_a ifself.tracks[k].time_since_update == 1]unmatched_tracks_a = [k for k in unmatched_tracks_a ifself.tracks[k].time_since_update != 1]matches_b, unmatched_tracks_b, unmatched_detections = \linear_assignment.min_cost_matching(iou_matching.iou_cost, self.max_iou_distance, self.tracks,detections, iou_track_candidates, unmatched_detections)# 整合所有的匹配对和未匹配的tracksmatches = matches_a + matches_bunmatched_tracks = list(set(unmatched_tracks_a + unmatched_tracks_b))return matches, unmatched_tracks, unmatched_detections# 级联匹配源码 linear_assignment.pydef matching_cascade(distance_metric, max_distance, cascade_depth, tracks, detections,track_indices=None, detection_indices=None):...unmatched_detections = detection_indicematches = []# 由小到大依次对每个level的tracks做匹配for level in range(cascade_depth):# 如果没有detections,退出循环if len(unmatched_detections) == 0:break# 当前level的所有tracks索引track_indices_l = [k for k in track_indices iftracks[k].time_since_update == 1 + level]# 如果当前level没有track,继续if len(track_indices_l) == 0:continue# 匈牙利匹配matches_l, _, unmatched_detections = min_cost_matching(distance_metric, max_distance, tracks, detections,track_indices_l, unmatched_detections)matches += matches_lunmatched_tracks = list(set(track_indices) - set(k for k, _ in matches))return matches, unmatched_tracks, unmatched_detections
卡尔曼滤波更新阶段
对于每个匹配成功的track,用其对应的detection进行更新,并处理未匹配tracks和detections:
# tracker.pydef update(self, detections):"""Perform measurement update and track management.Parameters----------detections: List[deep_sort.detection.Detection]A list of detections at the current time step."""# 得到匹配对、未匹配的tracks、未匹配的dectectionsmatches, unmatched_tracks, unmatched_detections = self._match(detections)# 对于每个匹配成功的track,用其对应的detection进行更新for track_idx, detection_idx in matches:self.tracks[track_idx].update(self.kf, detections[detection_idx])# 对于未匹配的成功的track,将其标记为丢失for track_idx in unmatched_tracks:self.tracks[track_idx].mark_missed()# 对于未匹配成功的detection,初始化为新的trackfor detection_idx in unmatched_detections:self._initiate_track(detections[detection_idx])...
参考
https://arxiv.org/abs/1703.07402
https://github.com/ZQPei/deep_sort_pytorch
https://towardsdatascience.com/computer-vision-for-tracking-8220759eee85
下载1:OpenCV黑魔法
在「AI算法与图像处理」公众号后台回复:OpenCV黑魔法,即可下载小编精心编写整理的计算机视觉趣味实战教程
下载2 CVPR2020
在「AI算法与图像处理」公众号后台回复:CVPR2020,即可下载1467篇CVPR 2020论文
个人微信(如果没有备注不拉群!)
请注明:地区+学校/企业+研究方向+昵称
觉得有趣就点亮在看吧


