正态分布在机器学习中为何如此重要？

从中心极限定理到正态分布

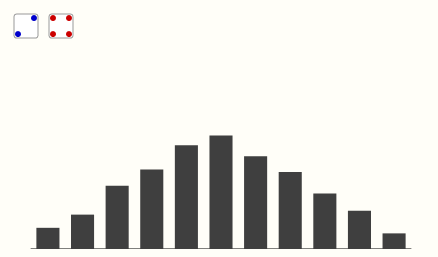
众所周知 ：一颗骰子每个面的概率相等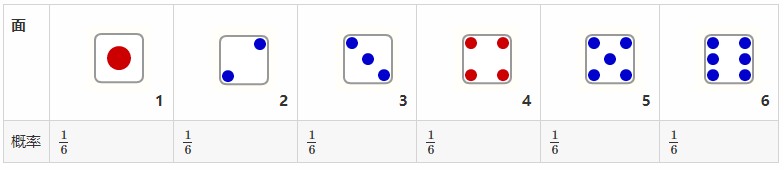两个骰子面值之和的概率，是两个骰子独立事件的概率的和。比如，得到点数3的概率为：一颗1、一颗2的概率 加上 一颗2、一颗1的概率 之和：

P(1)P(2)+P(2)P(1)=1/6×1/6+1/6×1/6=1/18 

对所掷的点数求和并将数值在坐标轴上标记出来，当掷出次数增大到无限时，坐标轴上的散点就会呈现出“正态分布”的形式。

这就是概率统计中大名鼎鼎的中心极限定理：如果样本量足够大，则变量均值的采样分布将近似于正态分布，而与该变量在总体中的分布无关。根据中心极限定理，如果一个事物受到多种因素的影响，不管每个因素本身是什么分布，它们加总后，结果的平均值就是正态分布。

from：高数叔（gaoshudashu666）

正态分布是一个在数学、物理及工程等领域都非常重要的概率分布，在统计学的许多方面有着重大的影响力。概率密度函数如下：

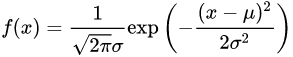正态分布概率密度函数

正态分布只依赖于数据集的两个特征：样本的均值和方差，非常简单而又容易被解释和理解。在大多数自然事件中，当数据量大到一定程度时，数据往往都近似服从于正态分布。比如：男女身高、寿命、血压、考试成绩、测量误差等等。

在实际运用中，我们更关注数据集的期望和方差这些特征量。当我们求出了期望与方差，可以利用中心极限定理转换为正态分布。

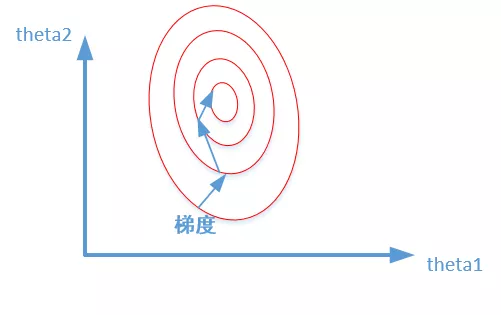
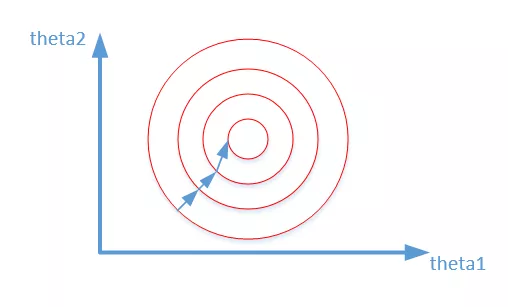
正态分布在机器学习中为何如此重要

在机器学习和深度学习中，我们经常要对输入的数据做归一化或者在隐藏层使用Batch-Normlization（BN）操作，将数据范围缩放到[0,1]或者[-1, 1]之间，主要作用：可以加快神经网络训练速度，防止过拟合。然而无论做归一化还是BN处理，虽然将数据的均值变为0，方差变为1，但是数据的整体分布并不一定服从标准的正态分布（实际数据大部分时候都不会是），做归一化和BN时，我们求出来的均值和方差，并不能说明我们数据是服从正态分布的。

检查特征是否满足正态分布

判断特征是否符合正态分布可以使用直方图、KDE分布图、Q-Q 图等等。

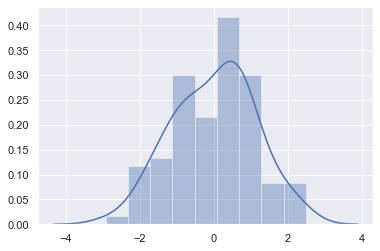
直方图和KDE分布图可以比较直观的看出数据样本本身的分布特征，推荐seaborn中的distplot，它的主要功能是绘制单变量的直方图，且还可以在直方图的基础上加入kdeplot和rugplot的部分内容，是一个功能非常强大且实用的函数。

sns.distplot(a, bins=None, hist=True, 
kde=True, rug=False, fit=None, hist_kws=None, 
kde_kws=None, rug_kws=None, fit_kws=None, 
color=None, vertical=False, norm_hist=False, 
axlabel=None, label=None, ax=None)

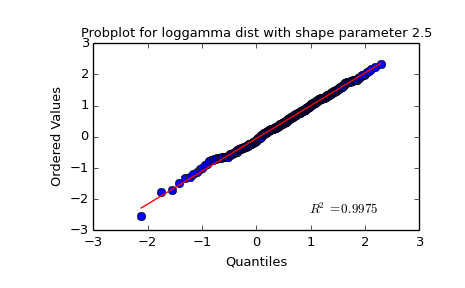
QQ-图用于直观验证一组数据是否来自某个分布，或者验证某两组数据是否来自同一（族）分布。如果两个分布相似，则该Q-Q图趋近于落在y=x线上。如果两分布线性相关，则点在Q-Q图上趋近于落在一条直线上，但不一定在y=x线上。

fig = plt.figure()
ax = fig.add_subplot(111)
x = stats.loggamma.rvs(c=2.5, size=500)
stats.probplot(x, dist=stats.loggamma, sparams=(2.5,), plot=ax)
ax.set_title("Probplot for loggamma dist with shape parameter 2.5")

数据变化方法：Box-Cox

Box-Cox变换是是统计建模中常用的一种数据变换，用于连续的响应变量不满足正态分布的情况。Box-Cox变换之后，可以一定程度上减小不可观测的误差和预测变量的相关性，可以明显地改善数据的正态性、对称性和方差相等性，对许多实际数据都行之有效。

from scipy import stats
from scipy.stats import norm, skew #for some statistics
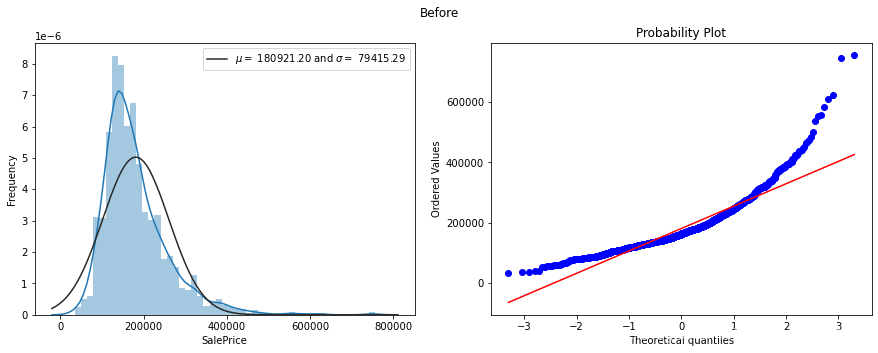
#查看SalePrice的skewness
fig=plt.figure(figsize=(15,5))
#pic1
plt.subplot(1,2,1)
sns.distplot(trains['SalePrice'],fit=norm)
(mu,sigma)=norm.fit(trains['SalePrice'])
plt.legend(['$\mu=$ {:.2f} and $\sigma=$ {:.2f}'.format(mu,sigma)],loc='best')
plt.ylabel('Frequency')
plt.subplot(1,2,2)
res=stats.probplot(trains['SalePrice'],plot=plt)
plt.suptitle('Before')

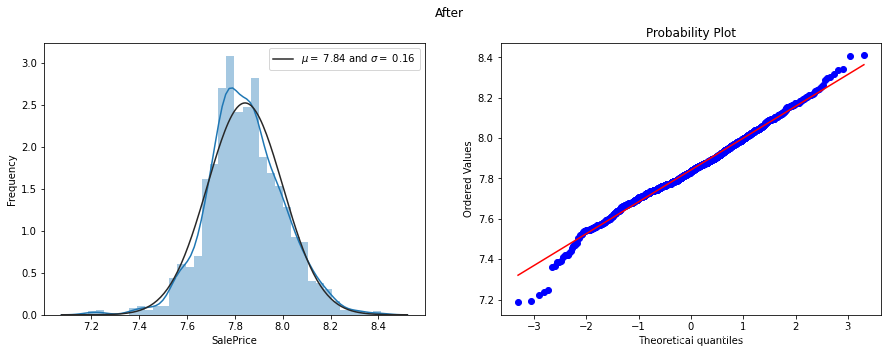
#进行Box-Cox变换
trains.SalePrice,lambda_=stats.boxcox(trains.SalePrice)

然后再看一下变换后的分布情况和QQ图

参考

https://www.lfhacks.com/t/dice-normal https://blog.csdn.net/qq_36653505/article/details/86618648 https://blog.csdn.net/weixin_42743978/article/details/88758003 https://blog.csdn.net/jim_sun_jing/article/details/100665967