海龟绘图案例分析之移动火柴变等式游戏（2）-技术圈

说在前面

移动一根火柴棒使等式成立，是一种简单有趣的智力游戏，只需具备简单的算术知识，就能参与游戏，老少皆宜，深受大家的喜爱。

上节课我和大家分享了创建题库的方法，并花了很大力气来介绍如何将结构相同的多段代码精简成循环语句，里面用到的一些技巧非常有趣，希望能对大家有所启发。

今天我们学习第二部分——绘制七段管算术表达式。

1.七段管数字

所谓七段管数字，就是用7个发光二极管来组成的阿拉伯数字。我们为这7个二极管按照从上到下、从左到右的顺序依次编号为0-6。部分数字所需二极管的编号如下图所示：

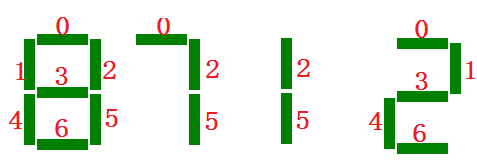
根据七段管数字的形状，我们可以创建字典digits来存储各数字所需二极管的编号，有digits ={0:(0,1,2,4,5,6),1:(2,5),2:(0,2,3,4,6),3:(0,2,3,5,6),4:(1,2,3,5),5:(0,1,3,5,6),6:(0,1,3,4,5,6),7:(0,2,5),8:(0,1,2,3,4,5,6),9:(0,1,2,3,5,6)}。

2.绘制单个二极管

使用turtle模块绘制二极管的方法很多，最简单的方法就是绘制一条线段。在本例中可以设置画笔粗细等于二极管的宽度，绘制与二极管等长的线段。因为不同编号的二极管方向不一样，需要考虑画笔的朝向，故操作比想象的要复杂。

另一种思路是把每个二极管都看作是矩形，可以根据二极管的长度d和宽度w，按照编号顺序，设置各二极管的左上角和右下角坐标（假设数字的左上角为坐标原点），并存储到列表x_y中，有x_y =[(w*5/4,0,w*5/4+d,-w),(0,-w/2,w,-w/2-d),(d+w*3/2+1,-w/2,d+w*5/2+1,-w/2-d),(w*5/4,-w/4-d,w*5/4+d,-w/4-d-w),(0,-w-d,w,-w-d*2),(d+w*3/2+1,-w-d,d+w*5/2+1,-w-d*2),(w*5/4,-w/2-d*2,w*5/4+d,-w*3/2-d*2)]。

由此可以根据二极管的坐标信息，绘制矩形并填充颜色（此外，确定各二极管的坐标范围，还为后面鼠标定位提供了方便）。自定义函数如下：

'''函数功能：根据左上角和右下角坐标绘制矩形并填充颜色函数名：draw_rectangle(x1, y1, x2, y2, c)参数表：x1, y1 -- 矩形的左上角坐标；       x2, y2 -- 矩形的右下角坐标；       c -- 画笔颜色。返回值：没有返回值。'''def draw_rectangle(x1, y1, x2, y2, c): #绘制某根二极管    tt.color(c)    tt.begin_fill()    tt.penup()    tt.goto(x1, y1)    tt.pendown()    tt.goto(x2, y1)    tt.goto(x2, y2)    tt.goto(x1, y2)    tt.goto(x1, y1)    tt.end_fill()

3.绘制单个七段管数字

有了字典digits和列表x_y，我们就可以调用draw_rectangle()函数在指定位置绘制单个七段管数字了。方法很简单，就是遍历digits[num]，依次绘制组成数字num的每根二极管即可。参考代码如下：

'''函数功能：根据给定的左上角坐标、长度、宽度和画笔颜色，利用字典digits绘制七段管数字num函数名：draw_num(x, y, d, w,c, num)参数表：x,y -- 七段管数字的左上角坐标；        d,w -- 二极管的长度和宽度；        c -- 画笔颜色；        num -- 要绘制的七段管数字。返回值：没有返回值。'''def draw_num(x, y, d, w, c,num): #绘制七段管数字    for i in digits[num]:  #digits[num]包含了组成数字num的所有二极管编号        draw_rectangle(x_y[i][0]+x,x_y[i][1]+y, x_y[i][2]+x, x_y[i][3]+y, c)

我们可以使用下列语句调用函数draw_num()，在不同位置绘制10个七段管数字：

for i in range(10):    draw_num(-500+i*(d+d),150, d, w, 'green', i)    draw_num(-500+i*(d+d),300, d, w,  'red', i)

效果图如下所示：

4.绘制七段管算术表达式

若想要绘制七段管算术表达式，就需要预先定义绘制运算符的函数。本案例中只考虑'+-='三种运算符。我们可以模仿七段管数字的绘制方法，将它们看作矩形组合，根据二极管的长度和宽度，规定好每个矩形的左上角和右下角坐标，调用draw_rectangle()函数绘制各个矩形即可。参考代码如下：

'''函数功能：根据给定的左上角坐标、边长和画笔颜色，绘制运算符op函数名：draw_operator(x, y, d,w, c, op)参数表：x,y -- 七段管数字的左上角坐标；        d,w -- 二极管的长度和宽度；        c-- 画笔颜色；        op -- 要绘制的运算符。返回值：没有返回值。'''def draw_operator(x, y, d, w,c, op): #绘制运算符    if op == '-':        draw_rectangle(x+w, y-w/4-d, x+w+d,y-w/4-d-w, c)    elif op == '+':        draw_rectangle(x+w, y-w/4-d, x+w+d,y-w/4-d-w, c)        draw_rectangle(x+w/2+d/2, y-w*3/4-d/2,x+w/2+d/2+w, y-w*3/4-d/2-d, c)    elif op == '=':        draw_rectangle(x+w, y+w*5/4-d, x+w+d,y+w/4-d, c)        draw_rectangle(x+w, y-w*7/4-d, x+w+d,y-w*11/4-d, c)

至此，我们完成了所有准备工作，可以绘制算术表达式了。先创建一个存储了算术表达式的字符串exp，然后遍历exp，调用draw_num()函数绘制数字，调用draw_operator()函数绘制运算符，参考代码如下：

exp = '3+6-5=4'for i, ch in enumerate(exp):    if ch in '+-=':       draw_operator(-500+i*(d+d), 0, d, w, 'red', ch)    else:        ch = int(ch)       draw_num(-500+i*(d+d), 0, d, w, 'red', ch)

效果图如下所示：

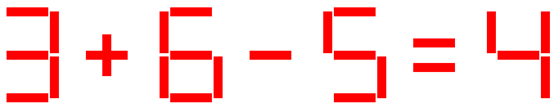
5.程序升级

上述程序能够绘制七段管算术表达式，但还没有实现游戏中“移动火柴棒”功能，因为它只有一支画笔。要想独立绘制或清除每一根火柴棒（二极管），我们需要为每根火柴棒（二极管）都创建一支画笔。

人生没有白走的路，每一步都算数。每一个项目的编程经验都可以迁移到新项目中。有了前面的铺垫，我们可以顺利地完成“火柴棒算式”的绘制工作。

6.设置各火柴棒坐标

因为“火柴棒算式”的格式是固定的，形如a+b=c或a-b=c。所以我们可以事先设置好组成算式的各火柴棒的左上角和右下角坐标，以便今后绘图。

前面我们介绍了存储单个七段管数字信息的列表x_y，我们可以在它的基础上依次存储数字a,b,c的全部二极管坐标信息，再把构成运算符的二极管坐标信息也存储起来。每个数字和运算符之间距离为2*d，在数字a的基础上分别向右平移4*d和8*d，即可得到数字b和c的二极管坐标信息。

由此我们可以得到组成“火柴棒算式”的总共25根火柴棒（二极管）的坐标信息（即矩形的左上角和右下角坐标）。参考代码如下：

'''函数功能：设置组成算式的各火柴棒左上角和右下角坐标，以便今后绘图函数名：get_pos(x, y, d, w)参数表：d,w – 二极管的长度和宽度。返回值：返回存储了各火柴棒左上角和右下角坐标的列表。'''def get_pos(d, w): #设置组成算式的各火柴棒左上角和右下角坐标    #根据七段管的长度和宽度，设置各二极管的左上角和右下角坐标（以数字的左上角为坐标原点）    x_y =[(w*5/4,0,w*5/4+d,-w),(0,-w/2,w,-w/2-d),(d+w*3/2+1,-w/2,d+w*5/2+1,-w/2-d),(w*5/4,-w/4-d,w*5/4+d,-w/4-d-w),          (0,-w-d,w,-w-d*2),(d+w*3/2+1,-w-d,d+w*5/2+1,-w-d*2),(w*5/4,-w/2-d*2,w*5/4+d,-w*3/2-d*2)]       for i in (2, 4): #添加数字b和c各条边的左上角和右下角坐标，向右平移2*d        for j in range(7):           x_y.append((x_y[j][0]+i*2*d, x_y[j][1], x_y[j][2]+i*2*d, x_y[j][3]))    #组成运算符的各火柴棒左上角和右下角坐标（减号只有一条横线，加号再加一条竖线）    x_y.append((w+2*d,-w/4-d, w+d+2*d, -w/4-d-w))   x_y.append((w/2+d/2+2*d, -w*3/4-d/2, w/2+d/2+w+2*d, -w*3/4-d/2-d))    #组成等号的各火柴棒左上角和右下角坐标（等号有2条横线）    x_y.append((w+6*d,w*5/4-d, w+d+6*d, w/4-d))    x_y.append((w+6*d,-w*7/4-d, w+d+6*d, -w*11/4-d))    return x_y

7.绘制单根火柴棒

绘制单根火柴棒的函数与前面绘制单个二极管的函数几乎一模一样，唯一的区别就是：每根火柴棒都有单独的画笔，所以需要提供一个画笔对象。代码如下：

'''函数功能：根据左上角和右下角坐标绘制矩形并填充颜色函数名：draw_rectangle(x1, y1, x2, y2, c, mypen)参数表：x1, y1 -- 矩形的左上角坐标；       x2, y2 -- 矩形的右下角坐标；       c -- 画笔颜色；       mypen -- 该条边对应的画笔对象。返回值：没有返回值。'''def draw_rectangle(x1, y1, x2, y2, c, mypen): #绘制七段管的某条边    mypen.color(c)    mypen.begin_fill()    mypen.penup()    mypen.goto(x1, y1)    mypen.pendown()    mypen.goto(x2, y1)    mypen.goto(x2, y2)    mypen.goto(x1, y2)    mypen.goto(x1, y1)    mypen.end_fill()

8.绘制操作数

绘制操作数就相当于前面所讲的绘制单个七段管数字，区别在于a,b,c三个操作数的位置已经定下来了，我们可以根据其在算式字符串中的下标来找到构成它的火柴棒。

此外，已经存在的火柴棒不能被重复绘制，所以我们需要定义一个全局变量stick_flag，它是一个列表，存储了各火柴棒是否已经被绘制的信息——该列表记录的信息是移动火柴棒的凭据，避免重复绘制火柴棒或移动根本不存在的火柴棒。参考代码如下：

'''函数功能：根据某个操作数的起点坐标和它在算式字符串中的下标等信息，利用字典digits绘制该操作数函数名：draw_num(x, y, i, num, d, w, c)参数表：x, y -- 该操作数的左上角坐标；       i -- 该操作数在算式字符串中的下标；       num -- 该操作数的值；       d -- 七段管的边长，即火柴棒的长度；       w，c -- 画笔粗细和颜色。返回值：没有返回值，全局变量stick_flag记录用到了哪些火柴棒。'''def draw_num(x, y, i, num, d, w, c): #绘制某个操作数    global stick_flag #记录火柴棒是否已经被绘制    for j in digits[num]:#digits[num]包含了组成数字num的所有火柴棒编号        stick_flag[7*i+j]= True #编号为7*i+j的火柴棒已经被绘制       draw_rectangle(pos_map[7*i+j][0]+x,pos_map[7*i+j][1]+y,pos_map[7*i+j][2]+x,pos_map[7*i+j][3]+y,c,stick_pens[7*i+j])

9.绘制算式

我们可以先调用函数get_pos()获取组成“火柴棒算式”的总共25根火柴棒的坐标信息，并依次存储到列表pos_map中。然后根据各操作数和运算符在列表pos_map中的下标，依次绘制3个操作数、运算符和等号。代码如下：

'''函数功能：根据算式的起点坐标和画笔颜色，绘制算式exp函数名：draw_expression(x, y, c, exp)参数表：x, y -- 该算式的左上角坐标；       c -- 画笔颜色；       exp -- 表示算式的字符串，例如'a+b=c'。返回值：没有返回值，全局变量stick_flag记录用到了哪些火柴棒。'''      def draw_expression(x, y, c, exp): #绘制算式    global stick_flag #记录火柴棒是否已经被绘制     for i in (0, 1, 2): #先依次绘制3个操作数        draw_num(x, y, i,int(exp[i*2]), d, w, c)    for i in range(21,25):  #再依次绘制运算符和等号        if i == 22 andexp[1] != '+':            continue        stick_flag[i] =True   #编号为i的火柴棒已经被绘制      draw_rectangle(pos_map[i][0]+x,pos_map[i][1]+y,pos_map[i][2]+x,pos_map[i][3]+y,c,stick_pens[i])

有了这些自定义函数，我们就可以在主函数中设置全局变量的初始值，并调用函数绘制算式了。主函数部分代码如下：

import turtle as ttimport random tt.TurtleScreen._RUNNING =True  # 启动绘图，在IDE中运行加这句可避免报错tt.speed(0)tt.delay(0)#组成七段管数字所需管子的编号（按照从上到下、从左到右顺序）digits ={0:(0,1,2,4,5,6),1:(2,5),2:(0,2,3,4,6),3:(0,2,3,5,6),4:(1,2,3,5),         5:(0,1,3,5,6),6:(0,1,3,4,5,6),7:(0,2,5),8:(0,1,2,3,4,5,6),9:(0,1,2,3,5,6)}x0, y0 = -300, 250 #算式左上角坐标d, w = 50, 10  #七段管的长度和宽度pos_map = get_pos(d, w) #存储组成算术式的各火柴棒左上角和右下角坐标stick_flag = [False for i inrange(25)] #判断某根火柴棒是否已绘制，共25根火柴棒stick_pens = [tt.Pen() for iin range(26)] #为每一跟火柴棒设置一支画笔，共25根，再加一支写无解的画笔for p in stick_pens:    p.ht()#隐藏笔头    p.pensize(1)exp = '3+2=5'draw_expression(x0, y0,'red', exp) #绘制算式tt.done()

程序输出效果图如下所示：

课后作业

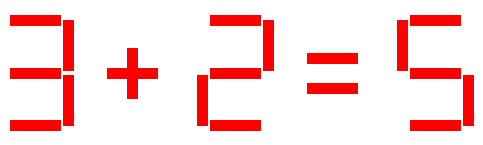
除了将每个二极管都看作是矩形，我在文中还提到了设置画笔粗细等于二极管的宽度，绘制与二极管等长的线段来表示二极管的方法。请根据此思路编写绘制七段管算术表达式的程序。参考效果图如下：

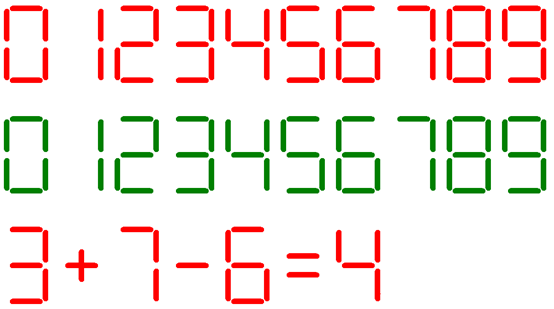
需要本文PPT、源代码和课后练习答案的，可以加入“Python算法之旅”知识星球参与讨论和下载文件，“Python算法之旅”知识星球汇集了数量众多的同好，更多有趣的话题在这里讨论，更多有用的资料在这里分享。

我们专注Python算法，感兴趣就一起来！

相关优秀文章：