原创 | 外部排序:如何用 2GB内存给 20 亿个整数排序?
来源公众号:帅地玩编程
作者:帅地
、
这篇文章在很久很久之前讲过,不过出了些小错误,今天把它修正了,并且从实战 + 漫画的方式带你领略外部排序魅力,并且让你知道外部排序的实现方式没有你想的那么简单。





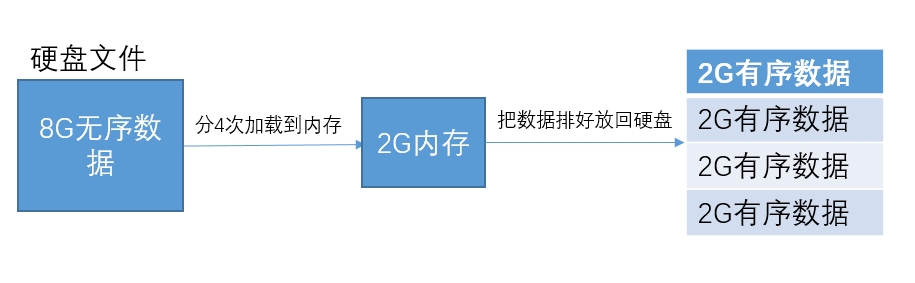
排序的时候我们可以选择快速排序或归并排序等算法。为了方便,我们把排序好的2G有序数据称之为有序子串吧。接着我们可以把两个小的有序子串合并成一个大的有序子串。

注意:读取的时候是每次读取一个int数,通过比较之后在输出。
按照这个方法来回合并,总共经过三次合并之后就可以得到8G的有序子串。



接下来把12个数据分成4份,然后排序成有序子串
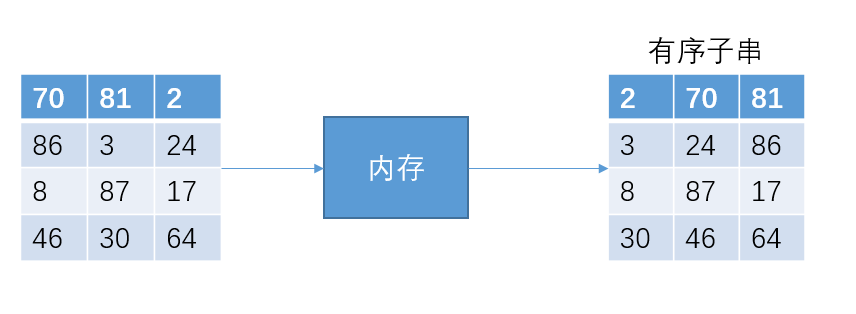
然后把子串进行两两合并
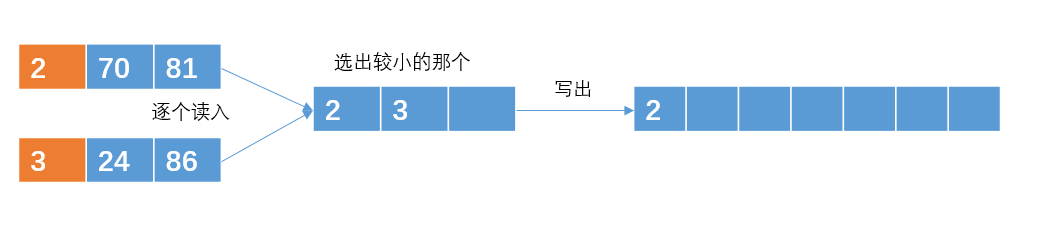
输出哪个元素,就在那个元素所在的有序子串再次读入一个元素
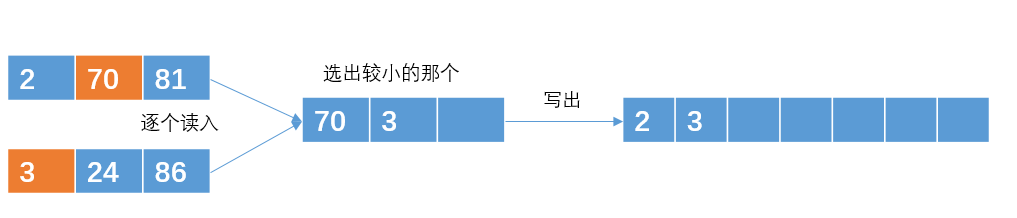
继续
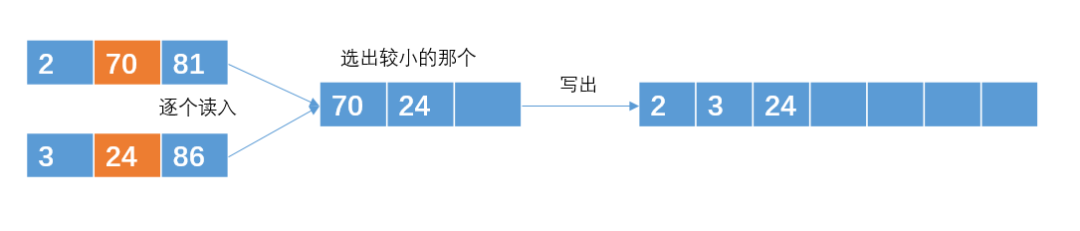
重复直到合并成一个包含6个int的有序子串
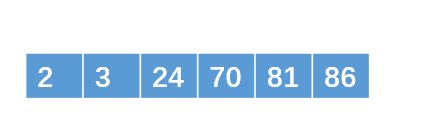
再把两个包含6个int的有序子串合并成一个包含12个int数据的最终有序子串
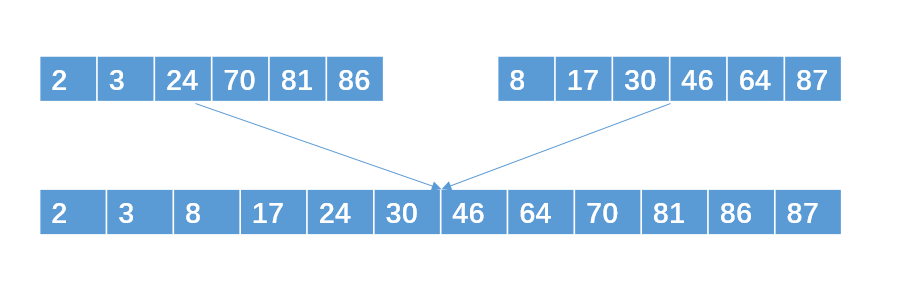

优化策略

解释下:例如对于数据2,我们把无序的12个数据分成有序的4个子串需要读写各一次,把2份3个有序子串合并成6个有序子串读写各一次;把2份6个有序子串合并从12个有序子串读写各一次,一共需要读写各3次。



多路归并
为了方便讲解,我们假设内存一共可以装4个int型数据。


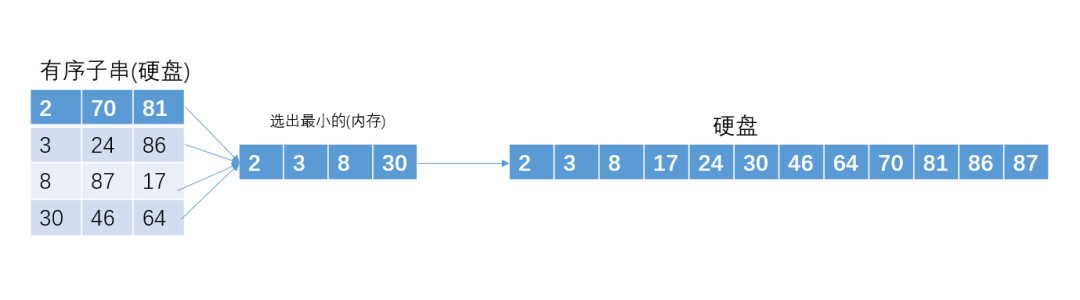




置换选择







例如我们可以从12个数据读取3个存到内存中,然后从内存中选出最小的那个数放进子串p1里;
之后再从在从剩余的9个数据读取一个放到内存中,然后再从内存中选出一个数放进子串p1里,这个数必须满足比p1中的其他数大,且在内存中尽量小。
这样一直重复,直到内存中的数都比p1中的数小,这时p1子串存放结束,继续来p2子串的存放。例如(这时假设内存只能存放3个int型数据):
12个无序的int数据

读入3个到内存中,且选出一个最小的到子串p1
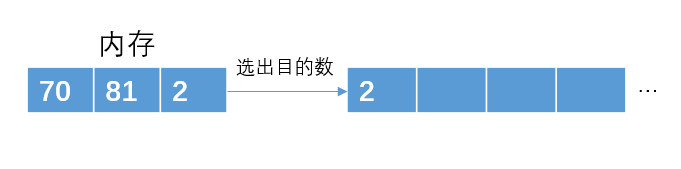
从内存中再次读取一个元素86
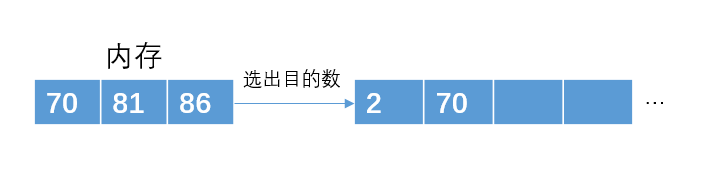
从内存中再次读取一个元素3
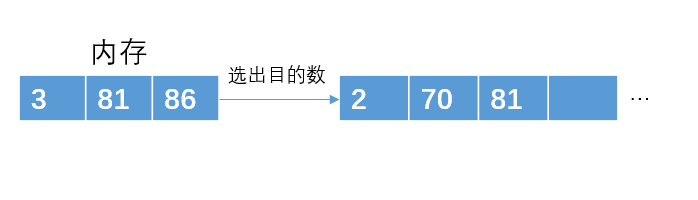
从内存中再次读取一个元素24
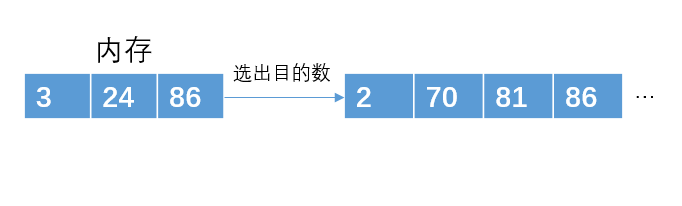
从内存中再次读取一个元素8
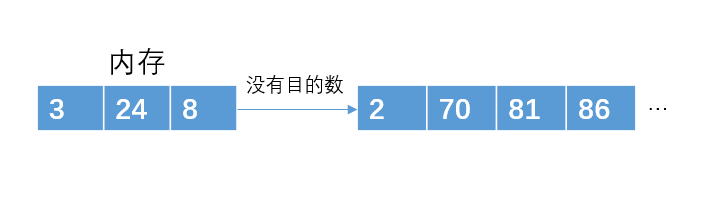
这个时候,已经没有符合要求的数了,且内存已满,进而用p2子串来存放,以此类推。
通过这种方法,p1子串存放了4个数据,而原来的那种方法p1子串只能存放3个数据。


(不知道堆排序的可以看下我之前写的文章:【算法与数据结构】堆排序是什么鬼?)
从12个数据中读取3个数据,构建成一个最小堆,然后从堆顶选择一个数写入到p1中。
之后再从剩余的9个数中读取一个数,如果这个数比刚才那个写入到p1中的数大,则把这个数插入到最小堆中,重新调整最小堆结构,然后在堆顶选一个数写入到p1中。
否则,把这个数暂放在一边,暂时不处理。之后一样需要调整堆结构,从堆顶选择一个数写入到p1中。
这里说明一下,那个被放在一边的数是不能再放入p1中的了,因为它一定比p1中的数都要小,所以它会放在下一个子串中
看这些文字会让人头大,我画图解释下吧。
从12数据读取3个数据

构建最小堆,且选出目标数
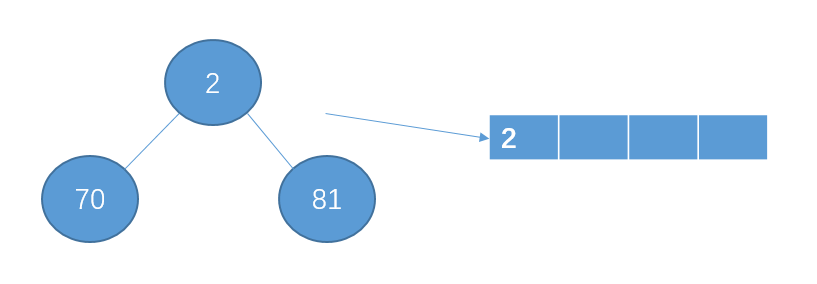
读入下一个数86
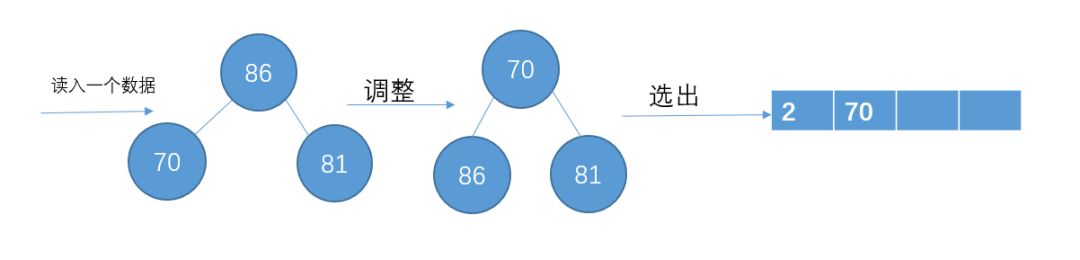
读入下一个数3,比70小,暂放一边,不加入堆结构中
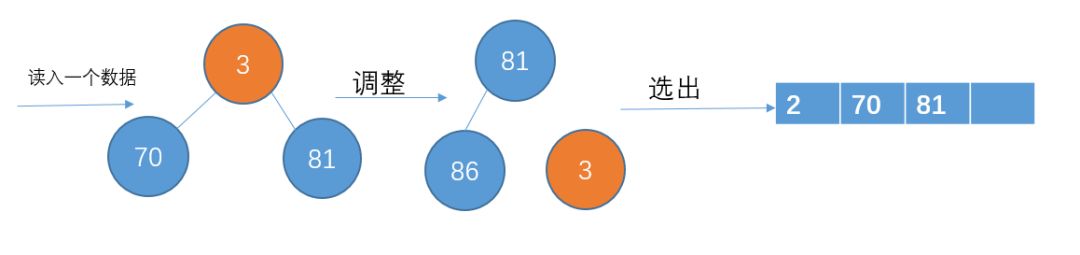
读入下一个数据24,比81小,不加入堆结构
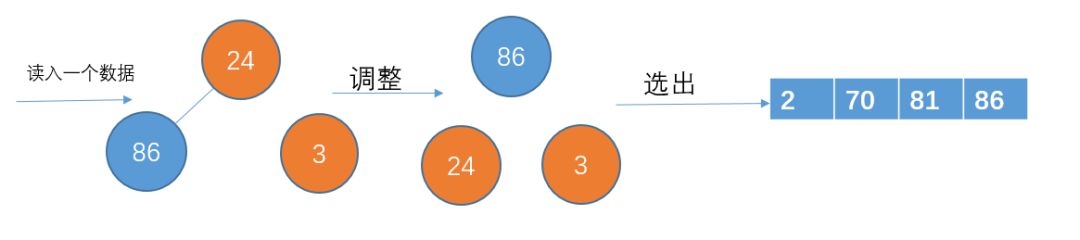
读入下一个数据8,比86小,不加入堆结构。此时p1已经完成了,把那些刚才暂放一边的数重新构成一个堆,继续p2的存放。
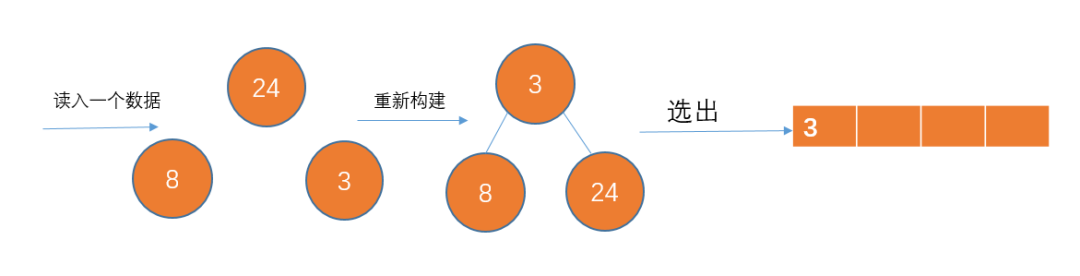
以此类推...
最后生成的p2如下:




这种方法适合要排序的数据太多,以至于内存一次性装载不下。只能通过把数据分几次的方式来排序,我们也把这种方法称之为外部排序

推荐阅读
