十大反直觉的数学结论
日期:2020年10月08日
正文共:2220字6图
预计阅读时间:6分钟
来源:超级数学建模
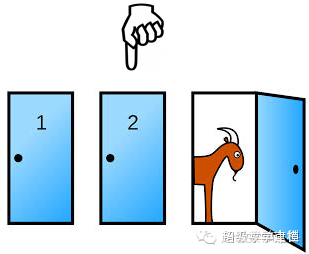
曾经问过很多人,几乎所有人都没有答对,换门的这一答案实在是太过反常识! 关于第一个解答这个问题的女士的经历也十分耐人寻味:
关于蒙提霍尔问题,玛丽莲·沃斯·莎凡特在她专栏的回答是改选会更有优势,这在美国引起了激烈的争议:人们寄来了数千封抱怨信,很多寄信人是科学老师或学者。一位来自佛罗里达大学的读者写道:“这个国家已经有够多的数学文盲了,我们不想再有个世界上智商最高的人来充数!真让人羞愧!”另一个人写道:“我看你就是那只山羊!”美国陆军研究所(US Army Research Institute)的埃弗雷特·哈曼(Everett Harman)写道,“如果连博士都要出错,我看这个国家马上要陷入严重的麻烦了。”但是莎凡特并没有错。最后她用整整4个专栏,数百个新闻故事及在小学生课堂模拟的测验来说服她的读者她是正确的。游戏秀的调查数据显示,那些改选的参赛选手赢的几率是那些没有改选的人的两倍,这证实了莎凡特在其第三篇专栏中的解释。
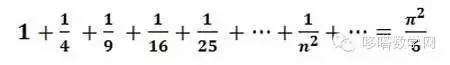



然而康托发现事实上上实数比有理数还要多。实数通常被认为是连续统,并且至今并能完全知道,是否有介于整数基数和连续统基数的无穷大?这个猜想被称为连续统猜想。
它的逻辑是这样的:

— THE END —

评论
