五十八、如何对一个数进行分解质因数
「@Author:Runsen」
❝编程的本质来源于算法,而算法的本质来源于数学,编程只不过将数学题进行代码化。「---- Runsen」
❞
先问你们一个小学问题:「什么是质因数?小学是对一个数进行分解质因数」
上次,我介绍了短除法,短除法其实是一种分解质因数的方法。
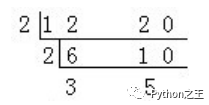
比如,12分解质因数为2*2*3,20分解质因数为2*2*5,
合数
合数是指在大于1的整数中除了能被1和本身整除外,还能被其他数(0除外)整除的数。与之相对的是质数,而1既不属于质数也不属于合数。最小的合数是4。
每个合数都可以写成几个质数相乘的形式,其中每个质数都是这个合数的因数,把一个合数用质因数相乘的形式表示出来,叫做分解质因数。如30=2×3×5 。分解质因数只针对合数。
合数分解质因数
把一个合数分解成若干个质因数的乘积的形式,即求质因数的过程叫做分解质因数。
分解质因数只针对合数。(分解质因数也称分解素因数)求一个数分解质因数,要从最小的质数除起,一直除到结果为质数为止。分解质因数的算式叫短除法,和除法的性质相似,还可以用来求多个数的公因式。
将需要分解的数字从2开始遍历,则分解的结果都会是质数。需要分解的数字是每一次上次分解之后的结果。比如,90有质因数2,之后用45分解质因数3,会得到15,15再去分解质因数3,最终得到的结果是:90=2*3*3*5。
L = []
num = int(input('请输入需要分解的数字:'))
for i in range(2,num):
while True:
if num%i == 0:
L.append(i)
num = num / i
else:
break
st = str(num)+'='
for i in L:
st = st + str(i) + '*'
print(st[:-1])
请输入需要分解的数字:90
90=2*3*3*5
下面将Python代码转化为Java代码
import java.util.Scanner;
/**
* @author Runsen
* @date 2020/12/9 13:18
*/
public class Decomposing_prime {
public static void main(String[] args) {
Scanner Sc = new Scanner(System.in);
System.out.print("请您输入一个数:");
int n = Sc.nextInt();
for (int i = 2; i <= n; i++) {
while (n % i == 0 && n != i) {
n /= i;
System.out.print(i + "*");
}
if (n == i) {
System.out.print(i);
break;
}
}
}
}
整合最小公倍数和最大公约数
下面对之前的最小公倍数和最大公约数,使用第四种方法分解质因数求出,
数字24 [2,2,2,3]和数字18 [2,3,3]的最大公约数就是两者质因数列表的所有公共部分,也就是6 [2,3]。因此问题就转化为取出[2,3]。
但是不能采用如下的算法计算:
a = [2,2,2,3]
b = [2,3,3]
c = []
for x in a:
if x in b:
c.append(x)
print(c) #[2,2,2,3] 不是[2,3]
显然这是错误的算法,正确的计算方法是,一旦进入了c列表的数字就应该从a列表和b列表中删除掉,避免重复计算。
a = [2,2,2,3]
b = [2,3,3]
c = []
while len(a):
x = a[0]
if x in b:
c.append(x)
b.remove(x)
a.remove(x)
print(c) #[2, 3]
根据质因数列表24 [2,2,2,3]和18 [2,3,3]
则计算24*18之积实际就是列表做加法[2,2,2,3]+[2,3,3]得到[2,2,2,2,3,3,3]
做除法,就是从[2,2,2,2,3,3,3]去除掉除数的质因数列表即可
24和18的最大公约数是[2,3],则最小公倍数就是从[2,2,2,2,3,3,3]去掉[2,3]
最终得到[2,2,2,3,3]就是最小公倍数。
遗憾的是,python中的列表不支持减法,也就是没有[2,2,2,2,3,3,3] - [2,3]这样的操作
但是两个列表之间能做加法,因此在做加法之前,先从一个列表中把两个列表中都有的可以成为公约数的内容从一个列表中删除掉,然后再让两个列表做加法即可,具体代码如下。
a = [2,2,2,3]
b = [2,3,3]
c = []
#求最小公倍数
for x in a:
if x in b:
b.remove(x)
c = a+b
c #[2, 2, 2, 3, 3]
因此得到最终的短除法求最小公倍数和最大公约数代码。
'''
@Author:Runsen
@WeChat:RunsenLiu
@微信公众号:Python之王
@CSDN:https://blog.csdn.net/weixin_44510615
@Github:https://github.com/MaoliRUNsen
@Date:2020/12/9
'''
def Decomposing_prime(num):
# 分解质因数
L = []
for i in range(2, num):
while True:
if num % i == 0:
L.append(i)
num = num / i
else:
break
return L
def f1(a,b):
# 求最大公约数的质因数
c = []
while len(a):
x = a[0]
if x in b:
c.append(x)
b.remove(x)
a.remove(x)
return c
def f2(a,b):
# 求最小公倍数的质因数
for x in a:
if x in b:
b.remove(x)
c = a + b
return c
def get_res(L):
result = 1
for i in L:
result = result * i
return result
if __name__ == '__main__':
x = int(input('请输入一个数字:'))
y = int(input('请输入一个数字:'))
res1 = f1(Decomposing_prime(x),Decomposing_prime(y))
res2 = f2(Decomposing_prime(x),Decomposing_prime(y))
print('最大公约数:' + str(get_res(res1)))
print('最小公倍数:' + str(get_res(res2)))
请输入一个数字:12
请输入一个数字:14
最大公约数:2
最小公倍数:84
❝本文已收录 GitHub,传送门~[1] ,里面更有大厂面试完整考点,欢迎 Star。
❞
Reference
传送门~: https://github.com/MaoliRUNsen/runsenlearnpy100
更多的文章
点击下面小程序
- END -

