趣说:如何对代码进行复杂度分析
你在学习数据结构算法的时候
你的目的就是为了让代码
运行的速度更加
“快”
占用的空间更加
“少”
那么当你看到一段代码的时候
你应该如何去分析它的运行效率?
在此之前
我们来看看你
不辞辛劳整理的文件夹
如果要让你在这个文件夹里面
让你找苍井空老师的教程
你会怎么找呢?
一种方式是
从第一个文件到最后一个文件
依次一个一个的查找
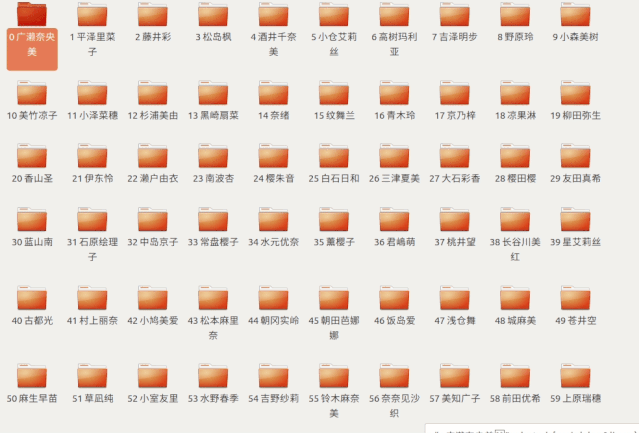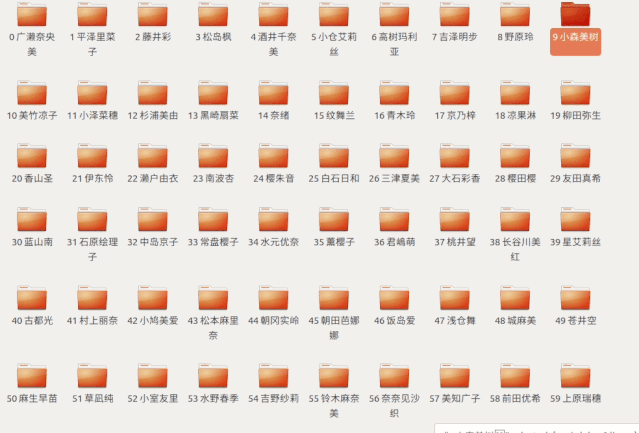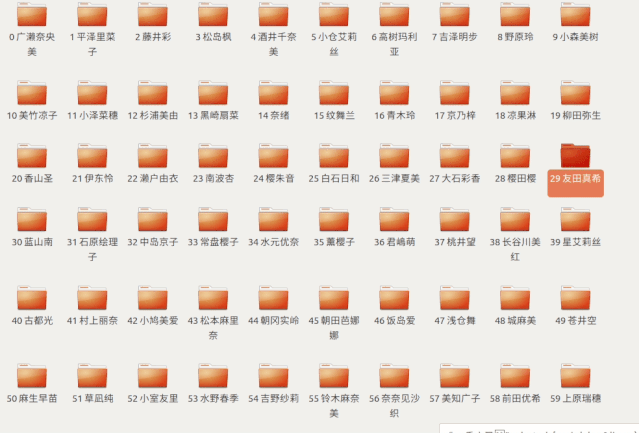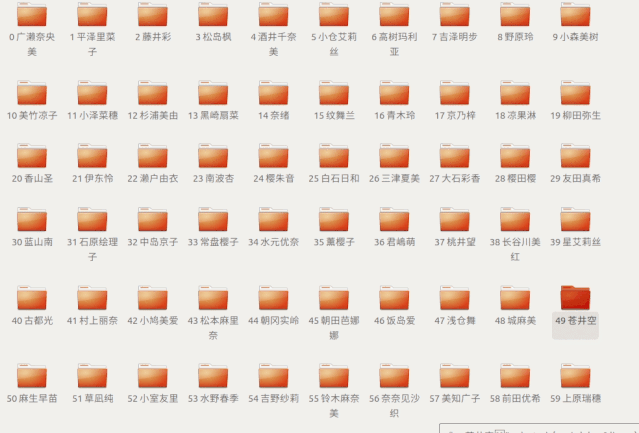
用代码体现就是这样
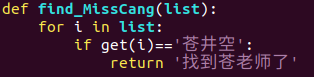
这样我们找到
第 50 个文件夹
发现是苍井空老师
于是进去开始观看了起来

不过这种查找效率并不高
另一种查找方式是这样
咱们先从中间开始找
如果发现小了
就把左边的都去掉
再在剩下的文件中往中间开始找
以此类推
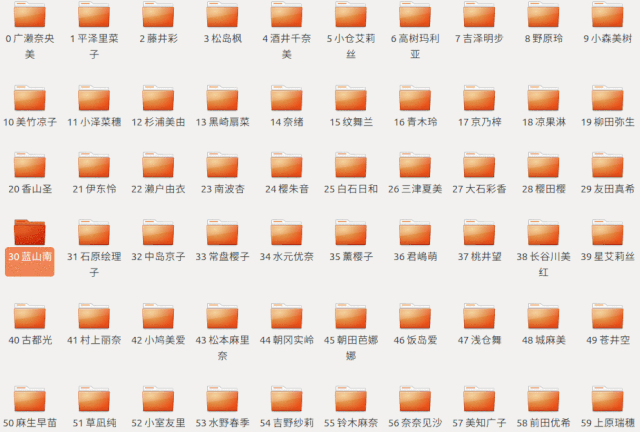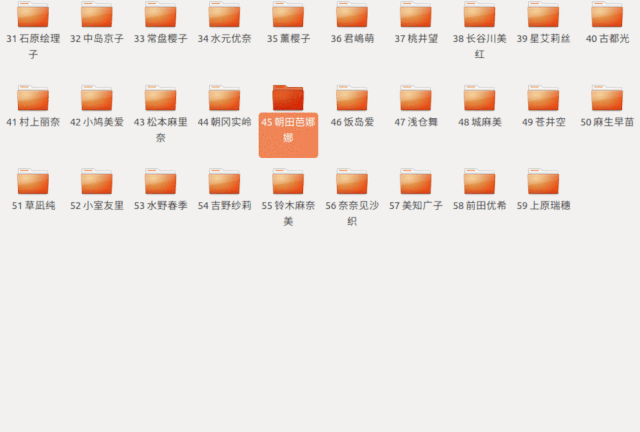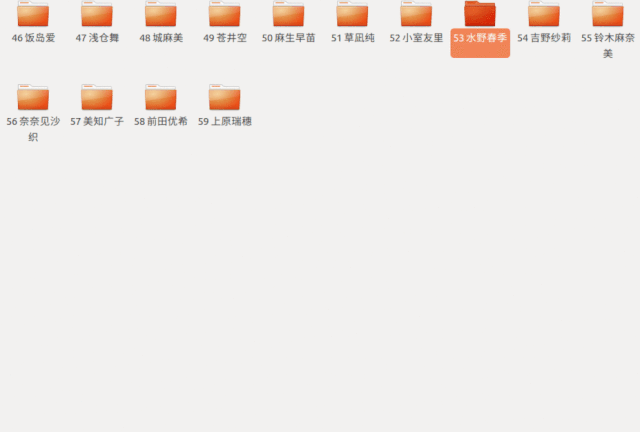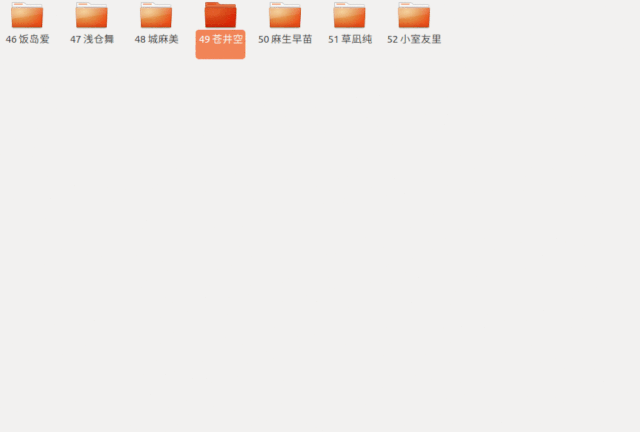
用代码体现就是这样
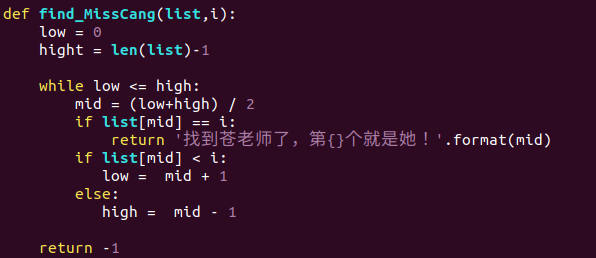
第一种查找方式
我们需要 50 次才找到苍井空
而第二种方式
我们只需要 4 次就找到了苍井空
是不是快了很多

其实第二种方式叫
“二分查找”
在有序列表中
是一种常见的算法
那这和我们要说的
代码复杂度分析
有什么关系嘛?

现在我们来假设
你的文件夹巨 TM 多
比如有上千万个文件夹
如果你按第一种方式去
找苍老师的话
你需要找 10000050 次
才能找到她

而你通过第二种方式去
找苍老师的话
你只需要 23 次
就能找到它
因为二分查找是一直折半查询
所以是 2 的对数
也就是 log10000060
到这里我们就会发现
随着数据规模的增加
代码的执行时间会跟着变化

那么如何去表示
不同算法之间的
时间复杂度呢?
可以使用
“大胸表示法”

不好意思
说错了
是
“大O表示法”
假设我们的文件夹
有 n 个这么多
那么第一种查找方式
用大 O 表示时间复杂度
就是这样
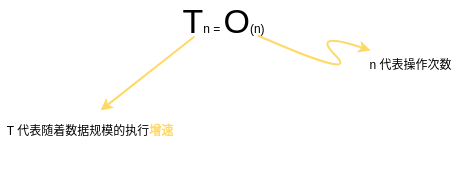
而第二种查找方式
用大 O 表示时间复杂度
就是这样
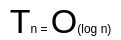
可以看到
执行时间的增速
和操作的次数成正比
以下这些是较为常见的
代码时间复杂度表示
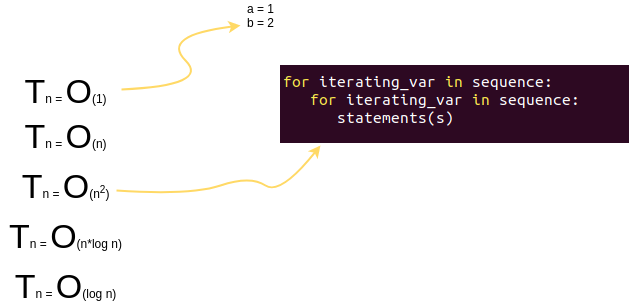
具体来说
复杂度排序是这样的
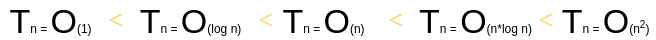
当你在分析一段代码的复杂度时
一般情况下
你只要往复杂的身上整就行了
比如
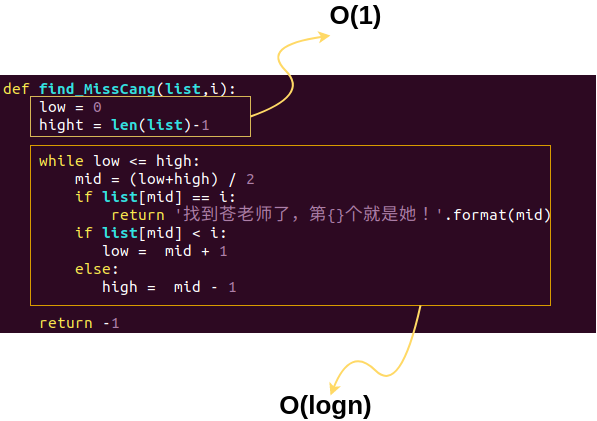
所以这段代码的复杂度
就是 O(logn)

最后你可能会问了
不对啊
如果苍井空老师的文件夹
在第一个位置
那使用第一种方式去查找
不就 1 次就能找着了

这时候效率
不就比二分查找快很多?
这就涉及到不同情况问题了
最好的情况就是苍老师在第 1 个位置
那么它的复杂度是 O(1)
最坏的情况就是苍老师在第 n 个位置
那么它的复杂度是 O(n)
这都是在极端情况下的分析
一般我们用一开始那样分析就行了
其它的在特定的情况下
差异比较大才需要考虑
最好最坏以及平均复杂度相关的
到时再具体情况具体分析好了
ok,以上就是
小帅b今天给你带来的分享
希望对你有帮助
那么我们下回再见
peace
推荐阅读

扫一扫
学习 Python 没烦恼
点个在看
给点动力
