（附论文）斯坦福助理教授马腾宇：ML非凸优化很难，如何破？

点击左上方蓝字关注我们

全网搜集目标检测相关，人工筛选最优价值内容

编者荐语

非凸优化问题被认为是非常难求解的，因为可行域内可能存在无数个局部最优，通常求解全局最优的算法复杂度是指数级的（NP 困难）。在近日的一篇文章中，斯坦福大学助理教授马腾宇介绍了机器学习中的非凸优化问题，包括广义线性模型、矩阵分解、张量分解等。

转载自 | 机器之心

作者 | 马腾宇

非凸优化在现代机器学习中普遍存在。研究人员设计了非凸目标函数，并使用现成的优化器（例如随机梯度下降及其变体）对其进行了优化，它们利用了局部几何并进行迭代更新。即使在最坏的情况下求解非凸函数都是 NP 困难的，但实践中的优化质量通常也不是问题，人们普遍认为优化器会找到近似全局最小值。

最近，在斯坦福大学助理教授马腾宇（Tengyu Ma）的一篇文章中，他为这种有趣的现象假设了一种统一的解释：实际使用目标的大多数局部最小值约为全局最小值，并针对机器学习问题的具体实例进行了严格地形式化。

文章地址：

https://arxiv.org/pdf/2103.13462.pdf

文章概览

优化非凸函数已成为现代机器学习和人工智能的标准算法技术。了解现有的优化非凸函数启发式方法非常重要，我们需要设计更有效的优化器。其中最棘手的问题是寻找非凸优化问题的全局极小值，甚至仅仅是一个 4 阶多项式——NP 困难。因此，具有全局保证的理论分析依赖于优化的目标函数的特殊属性。为了描述真实世界目标函数的属性特征，研究者假设机器学习问题的许多目标函数具有以下属性：全部或者绝大多数局部极小值近似于全局极小值。

基于局部导数的优化器可以在多项式时间内求解这一系列函数（下文讨论中也增加了一些额外的假设）。经验证据也表明机器学习和深度学习的实际目标函数可能具有这样的属性。

文章共分为七个章节，各章节主旨内容如下：

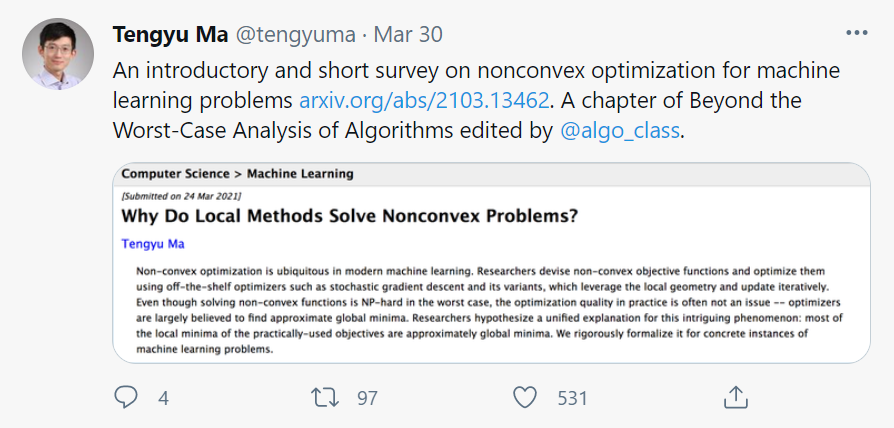
• 第一章：非凸函数的基本内容；

• 第二章：分析技术，包括收敛至局部极小值、局部最优 VS 全局最优和流形约束优化；

• 第三章：广义线性模型，包括种群风险分析和经验风险集中；

• 第四章：矩阵分解问题，包括主成分分析和矩阵补全；

• 第五章：张量分解，包括正交张量分解的非凸优化和全局最优；

• 第六章：神经网络优化的综述与展望。

文章细节

广义线性模型

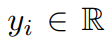第三章讲了学习广义线性模型的问题，并证明该模型的损失函数是非凸的，但局部极小值是全局的。在广义线性模型里，假设标签生成自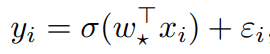，其中σ: R→R 是已知的单调激活函数，ε_i∈R 均为独立同分布（i.i.d.）的均值零噪声 (与 x_i 无关)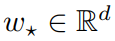，是一个固定的未知真值系数向量。

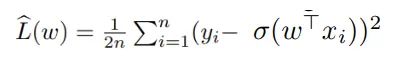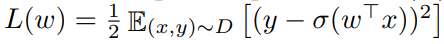研究者的目标是从数据中恢复ω*，然后最小化经验平方风险：。是相应的种群风险（population risk）。

该研究通过对其 landscape 属性的表征来分析的优化，分析路径包括两个部分：a) 所有种群风险的局部极小值都是全局极小值；b) 经验风险具有同样的属性。

不再是凸的。在本节其余部分中，研究者对这个问题进行了规律性假设。为了便于阐述，这些假设比必要的假设更为有力。当σ是恒等函数时，即σ（t）=t 为线性回归问题，损失函数是凸的。在实践中，人们已经把σ作为 sigmoid 函数，然后目标不再是凸的。在本节其余部分中，研究者对这个问题进行了规律性假设。为了便于阐述，这些假设比必要的假设更为有力。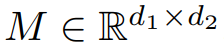

PCA 与矩阵补全

第四章讨论了基于矩阵分解的两个优化问题：主成分分析（PCA）和矩阵补全。它们与广义线性模型的根本区别在于，目标函数具有非局部极小或全局极小的鞍点。这意味着拟凸条件或 Polyak-Lojasiewicz（PL）条件不适用于这些目标。因此，需要更复杂的技术来区分鞍点和局部极小值。

主成分分析的一种解释是用最佳低秩近似来逼近矩阵。给出一个矩阵，求其最佳秩 r 逼近（Frobenius 范数或谱范数）。为了便于说明，研究者取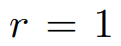，并假设 M 是维数为 d×d 的对称半正定。在这种情况下，最佳秩 1 近似的形式为。

矩阵补全是指从部分观测项中恢复低秩矩阵的问题，在协同过滤和推荐系统、降维、多类学习等方面得到了广泛的应用。研究者讨论了秩为 1 对称矩阵补全。

张量分解

第五章分析了另一个机器学习优化问题——张量分解。张量分解与矩阵分解或广义线性模型的根本区别在于，这里的非凸目标函数具有多个孤立的局部极小值，因此局部极小值集不具有旋转不变性，而在矩阵补全或主成分分析中，局部极小值集具有旋转不变性。这从本质上阻止只使用线性代数技术，因为它们本质上是旋转不变的。

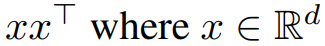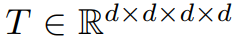研究者专注于一个最简单的张量分解问题——正交四阶张量分解。假设得到一个对称的 4 阶张量，它具有低秩结构，即：

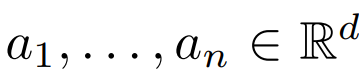其中。研究者的目的是恢复底层组件 a_1, . . . , a_n。他假设 a_1, . . . , a_n 是单位范数 R^d 中的正交向量，则目标函数为：

作者简介

马腾宇是斯坦福大学计算机科学和统计学助理教授。他本科毕业于清华大学计算机科学系，之后在普林斯顿大学获得计算机科学博士学位。期间，马腾宇师从 Sanjeev Arora 教授，并在多个国际顶级学术会议和期刊上发表近 20 篇高质量论文。

他的主要研究兴趣为机器学习和算法方面的研究，包括非凸优化、深度学习、强化学习、表征学习、分布式优化、凸松弛以及高维统计等。

个人主页：https://ai.stanford.edu/~tengyuma/

END

整理不易，点赞三连↓