二分查找树的应用及其画法

说在前面

在有序表中查找元素，通常使用二分查找算法，它每查找一次就可以缩小一半范围，效率远高于顺序查找。二分查找树是模拟二分查找过程绘制的一棵二叉树，通过图形将二分查找的过程可视化，有利于分析和理解抽象的算法问题，是一种非常重要的算法分析工具，在解决查找类问题中有着广泛的应用。

当数据量不大、查找范围较小时，使用手工绘制二分查找树是很方便的，但数据量较大时，手工绘图就不现实了；特别是在PPT展示或试卷印刷等场合中，需要的是规范美观的示意图，通常使用Photoshop或Graphviz等专业制图软件来绘制，耗时耗力，效果还不一定好。

Python内置turtle模块（海龟绘图）能以绘图形式动态展示程序运行过程，我们只需根据二分查找算法，编写相应递归函数，就能看到二分查找的动态过程，并最终获得一张精美的二分查找树图片。

猜数游戏是二分查找算法的典型应用，通常是由计算机生成一个随机整数让玩家来猜；也可以由玩家随意输入一个整数让计算机来猜，并根据计算机猜测的数据给出“偏大”或“偏小”的提示，直到计算机猜对为止。最后输出计算机猜测次数。因为一定范围内的整数是一个递增序列，故计算机常使用二分查找算法来寻找答案。

参考代码和程序运行界面如图1所示：

请问：（1）当输入整数16和48时，计算机猜测次数分别为多少？

（2）要想计算机最难猜中（猜测次数最多），玩家应该输入哪些整数？

要回答上述2个问题，可以根据题目代码，绘制出对应的二分查找树如图2所示：

可知，当输入16时，需要猜测5次；当输入48时，需要猜测6次；要想计算机最难猜中，玩家可以输入2,5,8,11,14,17,20,22,24,27,30,33,35,37,40,43,46,48,50中的某一个整数，最多猜测次数为6次。

当数据量不大、查找范围较小时，使用手工绘制二分查找树是很方便的，但如上图所示数据量较大时，手工绘图就不现实了；特别是在PPT展示或试卷印刷等场合中，需要的是规范美观的示意图，通常使用Photoshop或Graphviz等专业制图软件来绘制，耗时耗力，效果还不一定好。

Python内置turtle模块（海龟绘图）能以绘图形式动态展示程序运行过程，我们只需根据二分查找算法，编写相应递归函数，就能看到二分查找的动态过程，并最终获得一张精美的二分查找树图片。

1. 根据有序数组生成对分查找树节点信息

要画出二分查找树，必须记录各个节点的数据值和位置坐标，还有其父亲节点的信息，以便绘制该节点与父亲节点的连线。自定义函数create_bs(a:list)可以根据有序数组a生成存储了二分查找树各节点信息的二维列表res。其中列表res的元素为元组(data, x, y, f)，分别表示节点数据值、x、y坐标和其父亲节点在res中的下标。

一开始res是一个空列表，通过模拟对分查找过程，递归地访问数组a，将其元素值作为节点数据值，访问顺序号和递归层数分别作为节点的x、y坐标，当前节点在res中的下标即为其孩子节点的f值。因为根节点没有父亲节点，故设置其f值为-1。

参考代码如下所示：

def create_bs(a:list):    res = []    L, R = 0, len(a)-1    bs(a, res, L, R, 0, -1)#设置根节点的父亲节点下标为负数，表示没有父亲节点    return res

函数create_bs()调用了一个递归函数bs(a:list,res:list, L:int, R:int, y:int, f:int)，它有6个形式参数，其中a是存储了有序序列的一维列表；res是用来存储二分查找树节点信息的二维列表；L和R分别表示当前二叉树在有序数组中的左、右边界；y表示当前根节点的y坐标（高度）；f表示当前根节点的父亲节点在res列表中的下标。

函数bs()模拟了先序遍历二叉树的过程，先将根节点信息插入到列表res尾部，记录其下标tempf，再依次递归生成其左、右子树。其中根节点的值为a[m]，其下标m的计算体现了对分查找思想：当元素数量为偶数时，若左偏取中，则m = (L + R) // 2；若右偏取中，则m = (L + R + 1) // 2。

例如，当a=[1, 3, 5, 7, 9, 11, 13, 15, 17, 19]时，左偏取中和右偏取中对应的二分查找树分别如下图的图a和图b所示：

参考代码如下所示：

def bs(a:list,res:list, L:int, R:int, y:int, f:int):    if L > R: #空树        return    m = (L + R) // 2  #根节点在a中的下标，左偏取中    res.append([a[m], m, y, f]) #生成根节点信息    tempf = len(res) - 1 #当前节点为左右子树的父亲节点    if m > L: #若有左子树，则生成左子树        bs(a, res, L, m-1, y+1, tempf)    if m < R: #若有右子树，生成右子树        bs(a, res, m+1, R, y+1, tempf)

2. 绘制二分查找树示意图

生成二分查找树的各个节点信息以后，我们只需遍历列表res，就可以按照先序遍历二叉树的顺序，依次绘制各个节点和节点间连线。

我们设置自定义函数draw_bs(a:list)来绘制二分查找树，形式参数a表示存储了有序序列的一维列表。语句res = create_bs(a)通过调用函数create_bs(a)，将二叉树节点完整信息存储到二维列表res中。只需使用for循环遍历列表res，就能够实现按先序绘制二叉树各节点的功能。具体操作为调用函数draw_circle(x, y, r)在指定位置绘制半径为r的圆；调用函数write_data(x, y, r, data, size)在指定圆内书写数据data，其中size表示字体大小；若当前节点为非根节点，则调用函数draw_line(x1,y1, x2, y2, r)绘制其与父亲节点的连线。

为了灵活地控制图像的位置与大小，特别设置了四个变量disx, disy, magx, magy，分别表示横纵坐标的偏差和放大倍数。

参考代码如下所示：

def draw_bs(a:list):    res = create_bs(a)    disx, disy, magx, magy = 400, 200, 24, -50#分别表示横纵坐标的偏差和放大倍数    r = 15    write_data(-50, 300, 20, '生成对分查找树', 20)    write_data(0, 250, 20, ''.join(str(a)), 20)    time.sleep(1)    for v in res:        draw_circle(magx*v[1]-disx,magy*v[2]+disy, r)        write_data(magx*v[1]-disx,magy*v[2]+disy, r, v[0], 12)        if v[3] >= 0: #非根节点，与父节点连线            draw_line(magx*res[v[3]][1]-disx,magy*res[v[3]][2]+disy, magx*v[1]-disx, magy*v[2]+disy, r)          tt.ht()       tt.done() #x,y,r分别为圆心坐标和半径def draw_circle(x, y, r):    tt.penup()    tt.goto(x, y-r)    tt.pendown()    tt.circle(r)   #x,y,r,data分别为圆心坐标、半径和数据，size表示字体大小def write_data(x, y, r, data, size):    tt.penup()    tt.goto(x, y-r*0.7)    tt.pendown()    tt.write(data,align="center", font=("Arial", size, "normal"))

自定义函数draw_line(x1,y1, x2, y2, r)用来绘制节点间连线。其中(x1, y1)，(x2, y2)分别表示两个节点的圆心坐标，r为节点圆半径。我们先计算出两个节点的圆心距离d = ((x1-x2)*(x1-x2) + (y1-y2)*(y1-y2)) ** 0.5，然后取圆心连线与两个圆周的交点分别为(x3, y3)，(x4, y4)，如图4所示。计算出相关参数值后，将笔头抬起，先定位到(x3, y3)，再落笔将笔头移至(x4, y4)，实现画直线功能。

参考代码如下所示：

def draw_line(x1, y1, x2, y2, r): #绘制节点间连线    d = ((x1-x2)*(x1-x2) +(y1-y2)*(y1-y2)) ** 0.5    x3 = x1 + r * (x2-x1) / d    y3 = y1 + r * (y2-y1) / d    x4 = x2 - r * (x2-x1) / d    y4 = y2 - r * (y2-y1) / d    tt.penup()    tt.goto(x3, y3)    tt.pendown()    tt.goto(x4, y4)

三、总结

本文阐述了二分查找树在猜数游戏中的应用，以及二分查找树的绘制方法。程序仅利用二分查找基本算法和Python海龟绘图模块，就能绘制出与专业软件相媲美的精美图形，并根据实际需要动态生成各种二分查找树图片，方便快捷。

绘图程序本身就是对分查找和递归算法的典型应用，教师可以此作为教学内容。一方面利用程序绘制的图形学习二分查找树知识；另一方面要求学生根据算法原理，自行编写绘图程序，实现理论与实际的融合，提高计算思维和编程能力。

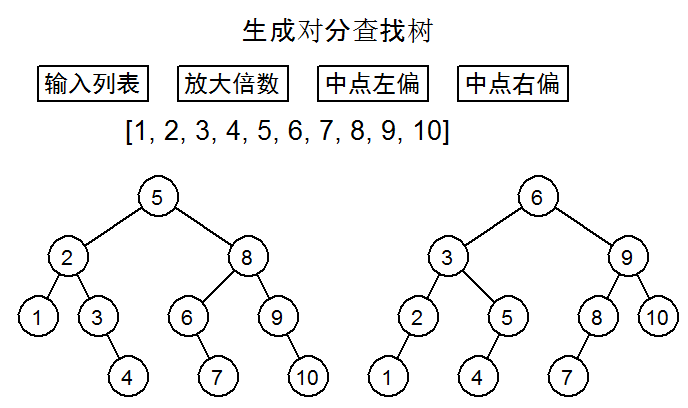
文章给出了绘制二分查找树的算法原理和相关代码，但并没有提供能实现演示视频所示的完整程序。请你参考视频演示效果，制作一个完整的绘制二分查找树程序，要求可以输入有序列表，调整放大倍数和设置中点左偏或右偏，并根据输入的x坐标偏差值，在屏幕的适当位置绘制二分查找树。

程序界面及运行效果如下图所示：

需要本文PPT、源代码和课后练习答案的，可以加入“Python算法之旅”知识星球参与讨论和下载文件，“Python算法之旅”知识星球汇集了数量众多的同好，更多有趣的话题在这里讨论，更多有用的资料在这里分享。

我们专注Python算法，感兴趣就一起来！

相关优秀文章：

阅读代码和写更好的代码

最有效的学习方式

Python算法之旅文章分类