CVPR2021-Representative BatchNorm
共 10889字，需浏览 22分钟
·
2021-04-14 00:08
源代码地址：https://github.com/ShangHua-Gao/RBN论文地址: Representative Batch Normalization with Feature Calibration
引言
BatchNorm模块能让模型训练更加稳定，因而被广泛使用。它的中心化以及缩放步骤需要依赖样本统计得到的均值和方差，而这也导致了在归一化的过程，忽视了各个实例的区别。其中，中心化步骤是为了增强信息特征，减少噪声。而缩放步骤是为了让特征服从一个稳定的分布。考虑到不同实例有不同特点，我们引入了简单有效的特征校准步骤（feature calibration scheme），改进得到Representative BatchNorm，在各大图像任务均有一定的提升。
BN的缺点
BatchNorm公式如下，它将特征缩放为一个均值为0，方差为1的分布
BatchNorm的一个前提是，我们假定了不同实例对应的特征都服从相同的分布。但实际中，存在以下两种情况不满足上述的假设：
一个mini-batch里的统计信息（均值，方差）与总的训练集/测试集的统计信息不一致 测试集中的数据实例不符合训练集的分布
针对第一点，BatchNorm在batchsize比较小的情况下，统计得到的均值和方差不够准确，相比其他Normalize方法（如GroupNorm）表现的很差。
而针对第二点，因为在推理过程中使用的是训练过程中统计更新的running-mean和running-variance。若测试集不与训练集在一个分布下，在BN后，它不一定服从的是均值为0，方差为1的分布。
针对不同情况，对模型的影响也不同
当测试集的均值小于running-mean，BN会错误地移除掉具有代表性的特征 当测试集的均值大于running-mean，BN会“漏掉”特征中的噪声 当测试集的方差小于running-var，BN会导致特征的intensity过小 当测试集的方差大于running-var，BN会导致特征的intensity过大
个人理解这里的intensity指的是特征强度，可能比较抽象，一方面指的是特征值的范围，另一方面也可以指特征的变化剧烈强度
为了解决上述的问题，一个很自然的想法是怎么将各个数据实例的特征，与mini-batch统计信息很好的结合在一起。一方面也能让特征处在稳定的分布，另一方面也能根据各个实例的特点进行进一步调整
Representative Batch Normalization
为了解决上述问题，我们提出了RBN，其中RBN也分为两个步骤，一个是中心化校准(Centering Calibration)，一个是缩放校准(Scaling Calibration)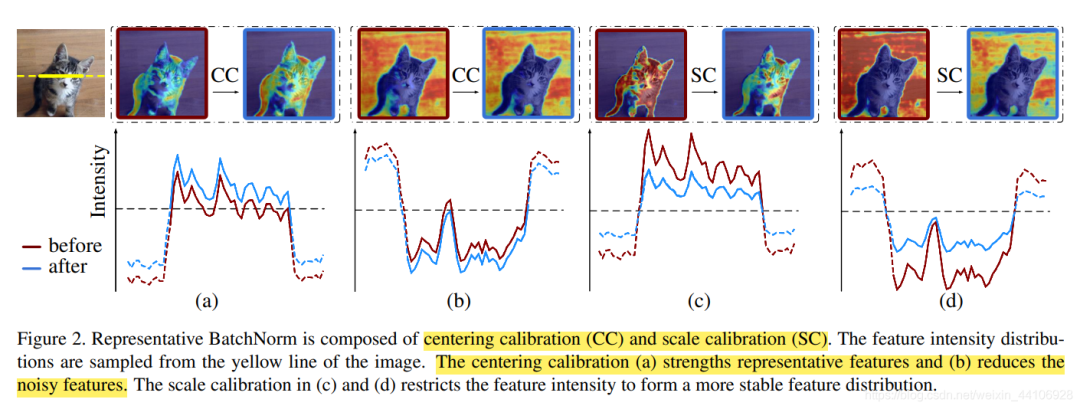
Centering Calibration
我们先看下公式
在对X求均值的时候，我们先对其做一个变换
其中 是输入特征， 则是一个形状为(N, C, 1, 1)的可学习变量， 则是表示各个实例的特征，它可以有多种shape（只要是合理的变换，能表征各个实例的特征即可），这里我们对输入使用一个全局平均池化来得到实例特征，因此形状为(N, C, 1, 1)。
我们首先将实例特征与可学习变量相乘，最后与输入进行相加
公式推导
对于使用全局平均池化得到实例特征，我们有如下的公式
因为后续我们要对变换后的X求均值（在BN里是对N,H,W这三个维度求均值），对于 来说，已经是X对HW维度上求过均值了，后续不过是在N的维度上再求一次均值。所以我们有
我们针对变换后的X求均值，有
然后我们来对比一下该变换带来的差异
我们将两个进行相减比较差异
可以看到，当 的绝对值接近于0， 和 的差值接近于0，说明此时还是依赖于batch内的统计信息。当 的绝对值较大，具体可以分以下两种情况来考虑
当 大于0，且 > ，此时Representative Feature得到增强，反之亦然 当 小于0，且 > ，此时特征噪声会抑制，反之亦然
Scaling Calibration
我们在BN后，拉伸调整之前做一次缩放对齐
公式如下：
其中 和 是两个可学习参数，用于拉伸平移（跟BN的两个可学习参数效果类似） 跟前面的类似，是一个实例特征，这里还是用全局平均池化得到。 则是一个限制函数，可以使用各种范数来限制，这里采用的是 sigmoid 函数来限制值域
公式推导
我们的限制函数是 sigmoid，于是有
那么我们可以找到一个 满足
可以看到我们的方差因为限制函数而变得更小了，让分布更加的均匀
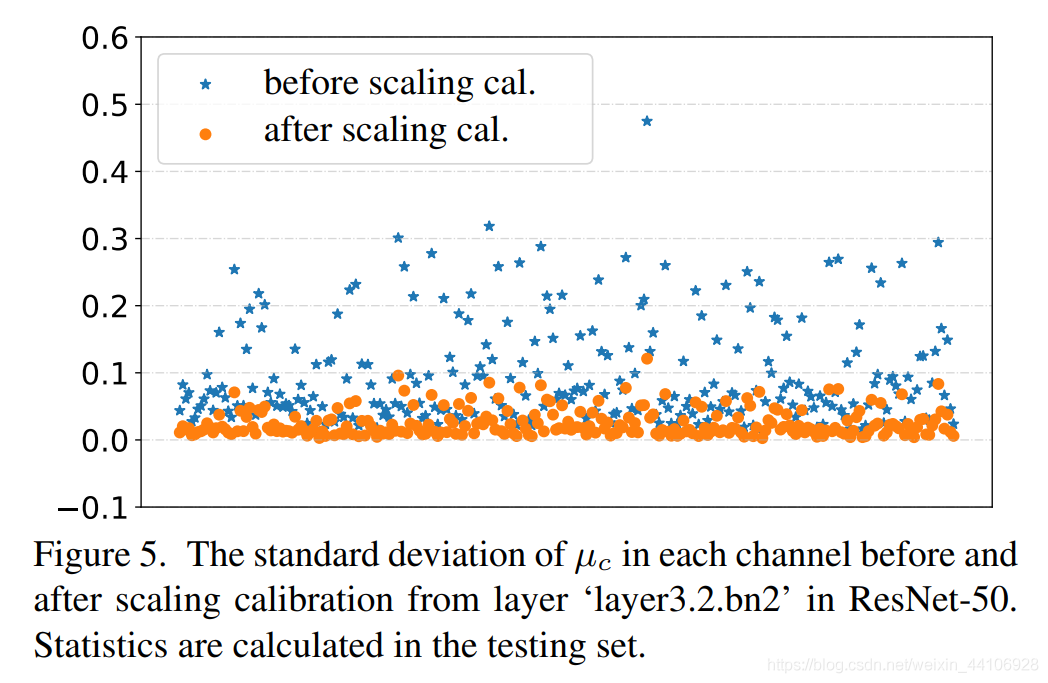
整体流程
首先对输入做中心校准
然后就是熟悉的减均值，除方差
接着是做缩放校准
最后是做拉伸，偏移，得到最终结果
实验对比
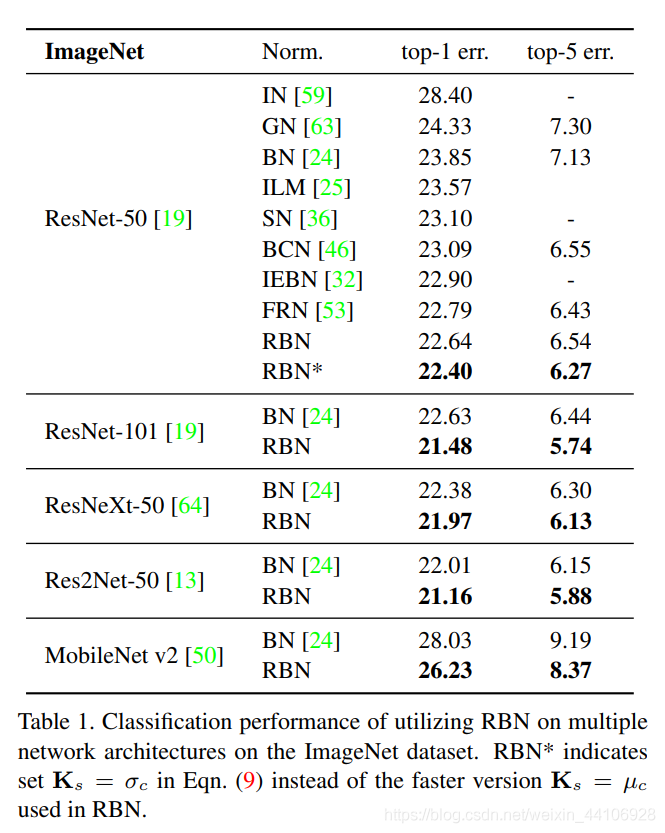作者在主流的网络里测试了常见的Normalize模块，并进行对比，可以看到提升还是比较显著的
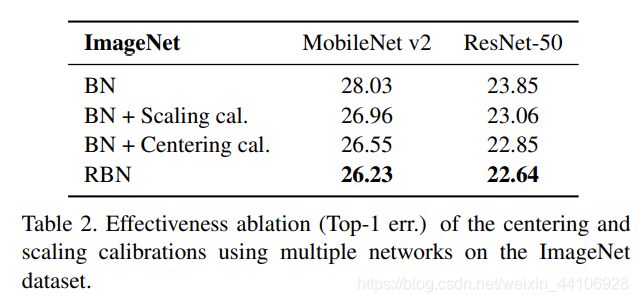另外也通过消融实验证明均值校准和缩放校准的有效性，另外更多实验可以看下原文。
代码
作者也开放了对应的Pytorch源码
import torch.nn as nn
import math
import torch
import numpy as np
import torch.nn.functional as F
class RepresentativeBatchNorm2d(nn.BatchNorm2d):
def __init__(self, num_features, eps=1e-5, momentum=0.1, affine=True,
track_running_stats=True):
super(RepresentativeBatchNorm2d, self).__init__(
num_features, eps, momentum, affine, track_running_stats)
self.num_features = num_features
### weights for affine transformation in BatchNorm ###
if self.affine:
self.weight = nn.Parameter(torch.Tensor(1, num_features, 1, 1))
self.bias = nn.Parameter(torch.Tensor(1, num_features, 1, 1))
self.weight.data.fill_(1)
self.bias.data.fill_(0)
else:
self.register_parameter('weight', None)
self.register_parameter('bias', None)
### weights for centering calibration ###
self.center_weight = nn.Parameter(torch.Tensor(1, num_features, 1, 1))
self.center_weight.data.fill_(0)
### weights for scaling calibration ###
self.scale_weight = nn.Parameter(torch.Tensor(1, num_features, 1, 1))
self.scale_bias = nn.Parameter(torch.Tensor(1, num_features, 1, 1))
self.scale_weight.data.fill_(0)
self.scale_bias.data.fill_(1)
### calculate statistics ###
self.stas = nn.AdaptiveAvgPool2d((1,1))
def forward(self, input):
self._check_input_dim(input)
####### centering calibration begin #######
input += self.center_weight.view(1,self.num_features,1,1)*self.stas(input)
####### centering calibration end #######
####### BatchNorm begin #######
if self.momentum is None:
exponential_average_factor = 0.0
else:
exponential_average_factor = self.momentum
if self.training and self.track_running_stats:
if self.num_batches_tracked is not None:
self.num_batches_tracked = self.num_batches_tracked + 1
if self.momentum is None: # use cumulative moving average
exponential_average_factor = 1.0 / float(self.num_batches_tracked)
else:
exponential_average_factor = self.momentum
output = F.batch_norm(
input, self.running_mean, self.running_var, None, None,
self.training or not self.track_running_stats,
exponential_average_factor, self.eps)
####### BatchNorm end #######
####### scaling calibration begin #######
scale_factor = torch.sigmoid(self.scale_weight*self.stas(output)+self.scale_bias)
####### scaling calibration end #######
if self.affine:
return self.weight*scale_factor*output + self.bias
else:
return scale_factor*output
其中大部分代码跟Pytorch自己实现的BatchNorm类似，我们简单关注几点
首先在初始化里，初始化了中心校准，缩放校准所需的可学习参数，并填充默认值
### weights for centering calibration ###
self.center_weight = nn.Parameter(torch.Tensor(1, num_features, 1, 1))
self.center_weight.data.fill_(0)
### weights for scaling calibration ###
self.scale_weight = nn.Parameter(torch.Tensor(1, num_features, 1, 1))
self.scale_bias = nn.Parameter(torch.Tensor(1, num_features, 1, 1))
self.scale_weight.data.fill_(0)
self.scale_bias.data.fill_(1)
我们经常会把可学习参数中，权重w初始化为1，偏置b初始化为0，而这里恰恰相反，将权重则初始化为0，偏置则为1。个人推测可以参考推导Centering Calibration中，当w为0时，则等价于原始的BN，从而后续让模型根据需要来去调整w。但为什么偏置设为1，笔者没想清楚。可以参考RBN开源工程的issue1，地址在这篇文章开头
然后是初始化我们的实例特征提取操作，这里是用一个全局池化
### calculate statistics ###
self.stas = nn.AdaptiveAvgPool2d((1,1))
在forward函数一开始，我们先做中心校准操作
####### centering calibration begin #######
input += self.center_weight.view(1,self.num_features,1,1)*self.stas(input)
####### centering calibration end #######
然后是调用torch自带的Batchnorm
...
output = F.batch_norm(
input, self.running_mean, self.running_var, None, None,
self.training or not self.track_running_stats,
exponential_average_factor, self.eps)
接着做缩放校准操作
####### scaling calibration begin #######
scale_factor = torch.sigmoid(self.scale_weight*self.stas(output)+self.scale_bias)
####### scaling calibration end #######
最后根据属性 self.affine 做最后的拉伸和偏移
if self.affine:
return self.weight*scale_factor*output + self.bias
else:
return scale_factor*output
总结
作者提出了一种简单有效的方法，将BN层的mini-batch的统计特征和各个实例独自的特征（Representative也就体现在这里）巧妙的结合起来，使得能够更好自适应集合里的数据，最后各个实验也证明了其有效性。期待更多在Norm方面的工作~
欢迎关注GiantPandaCV, 在这里你将看到独家的深度学习分享，坚持原创，每天分享我们学习到的新鲜知识。( • ̀ω•́ )✧
有对文章相关的问题，或者想要加入交流群，欢迎添加BBuf微信：