太牛了!98 年后浪科学家,首次挑战图片翻转不变性假设,一作拿下 CVPR 最佳论文提名

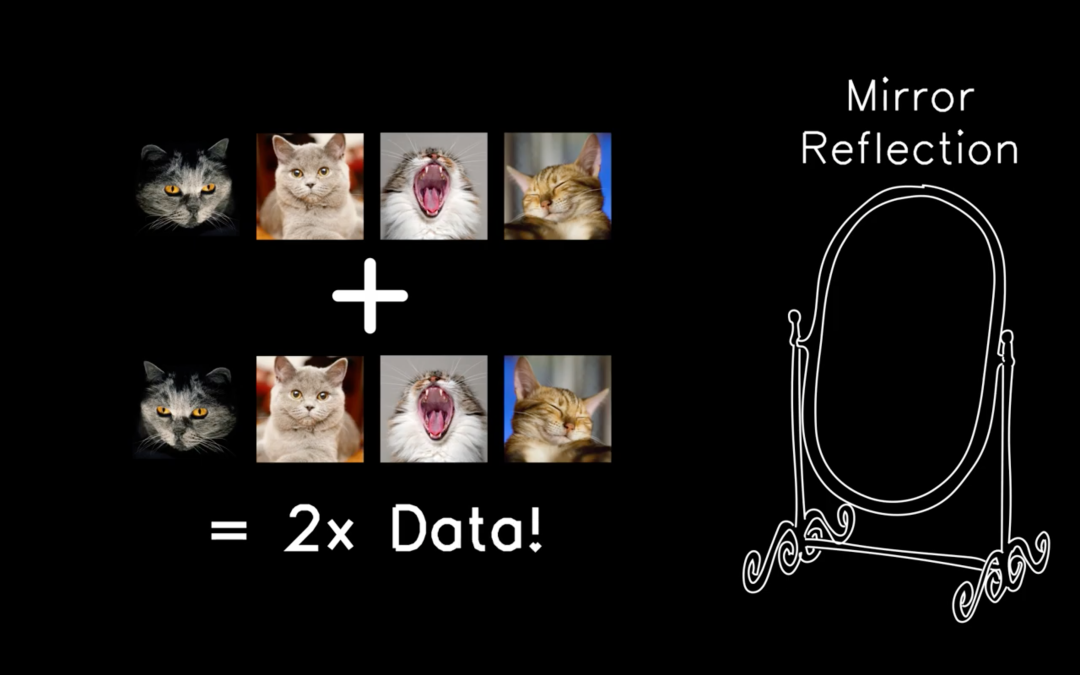


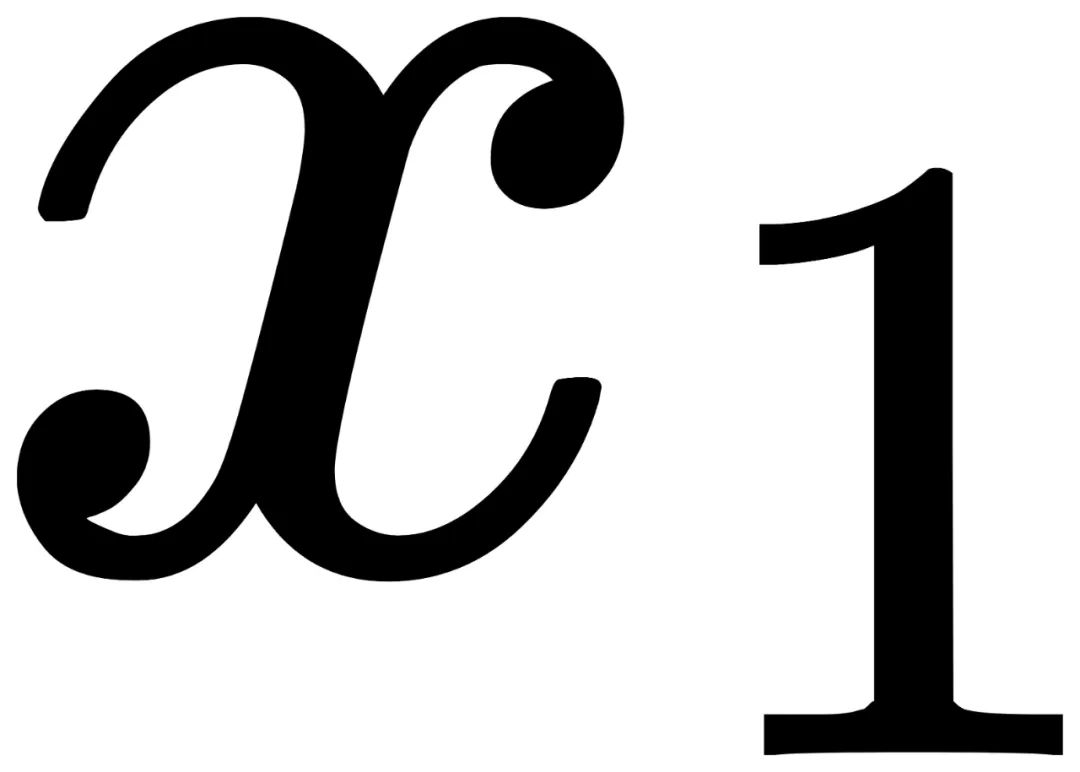 和
和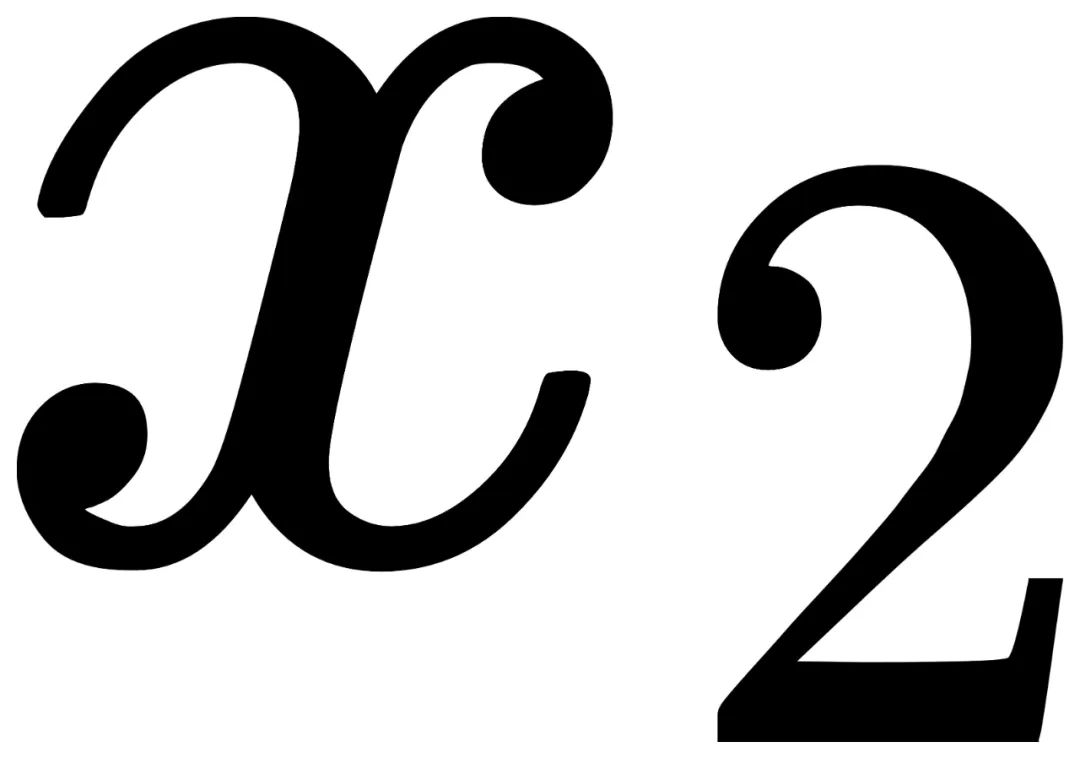 分别与
分别与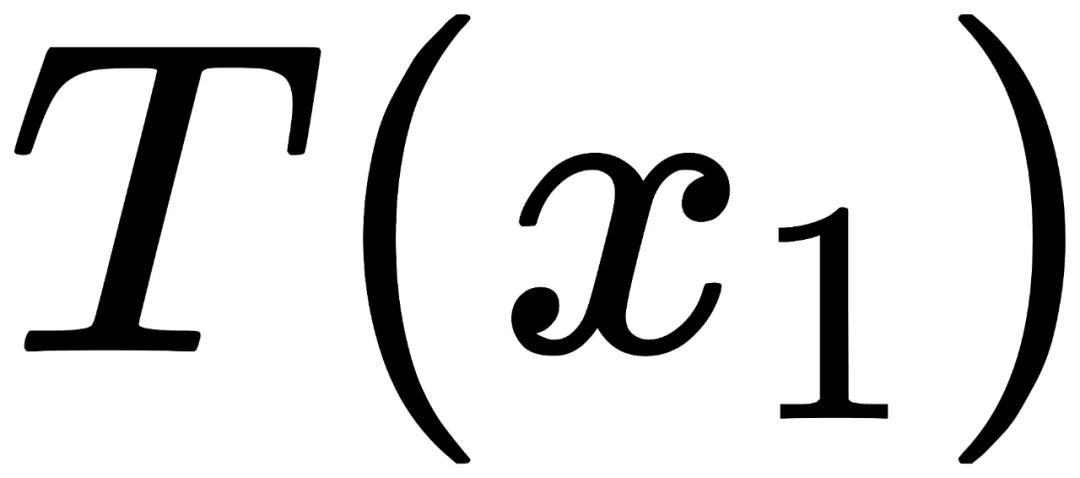 和
和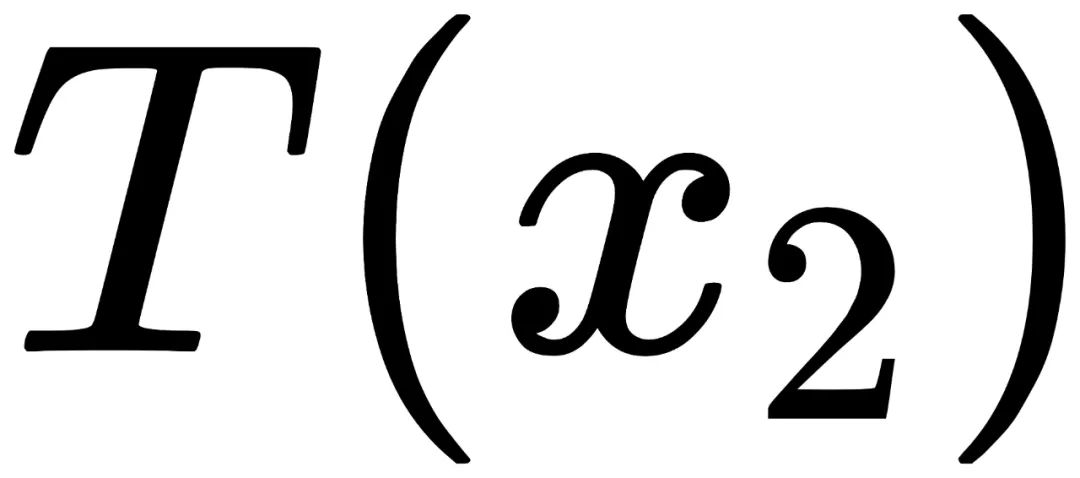 的出现概率不一致:
的出现概率不一致: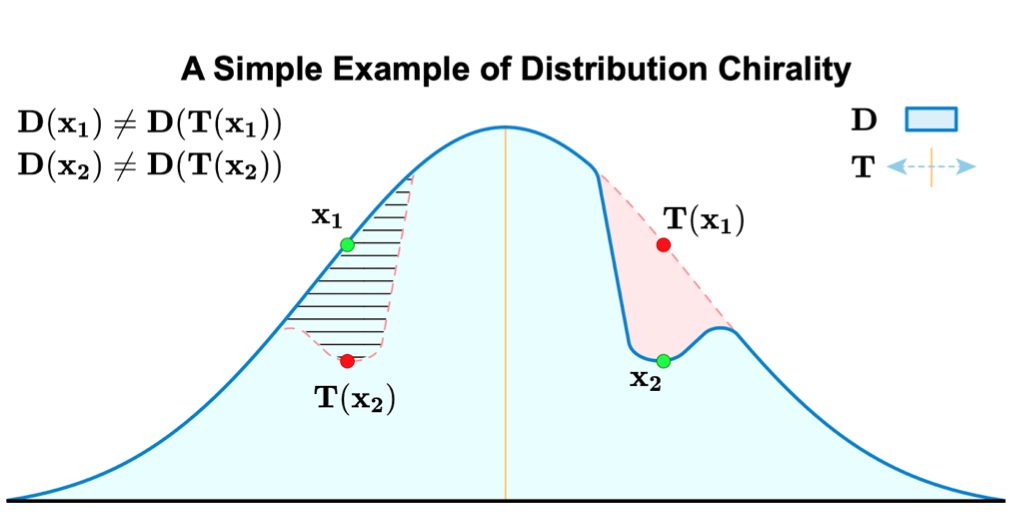

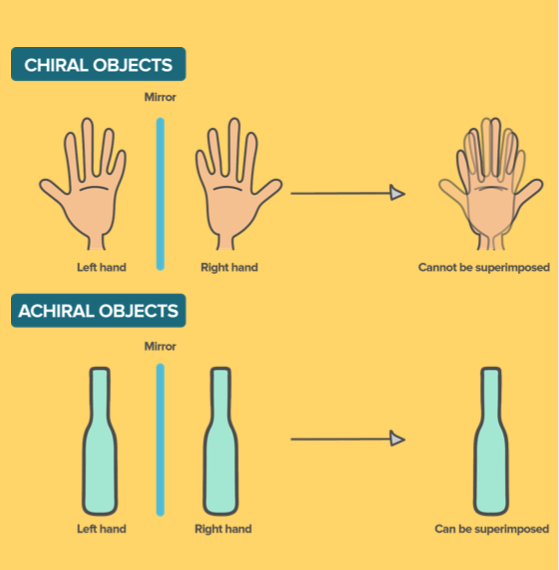
手性特征聚类方法
互联网图片集
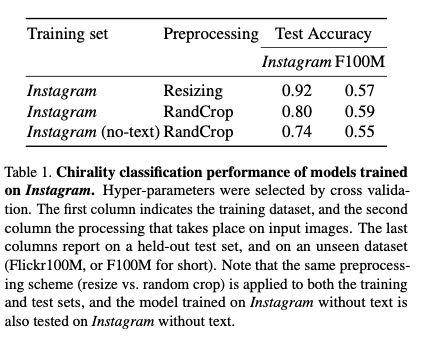










D为数据集所来源于的图像分布。 T为一个图像变换函数,例如镜像翻转。需要注意的是论文中的证明不仅限于镜像翻转,也可以被用于任何具备结合律(associativitive)和可逆性(invertible)的变换。 J为一个图像处理函数。例如去马赛克以及JPEG图片压缩。  为经过J处理后所得到的的新图像分布。
为经过J处理后所得到的的新图像分布。
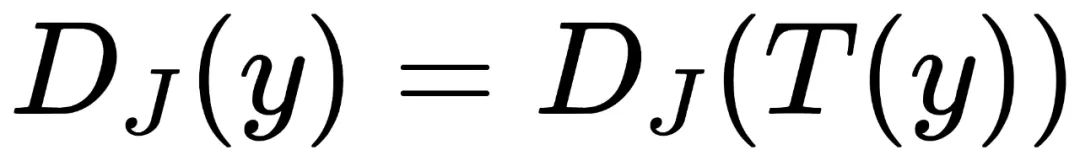 ,那么
,那么 同样不具备视觉手性。
同样不具备视觉手性。 也不具备视觉手性。换句话说,我们可以通过检查T和J的交换律,来判断数字图像处理能否造成视觉手性现象。
也不具备视觉手性。换句话说,我们可以通过检查T和J的交换律,来判断数字图像处理能否造成视觉手性现象。去马赛克(Demosaicing):数字相机的感光元件一般只能在每个像素格上捕捉RGB中的其中一种颜色,而其中最常用的为贝尔滤色镜(Bayer Color Filter Array),如下图所示。去马赛克则是将感光元件得到的二维图像还原为三维全彩的这一过程。 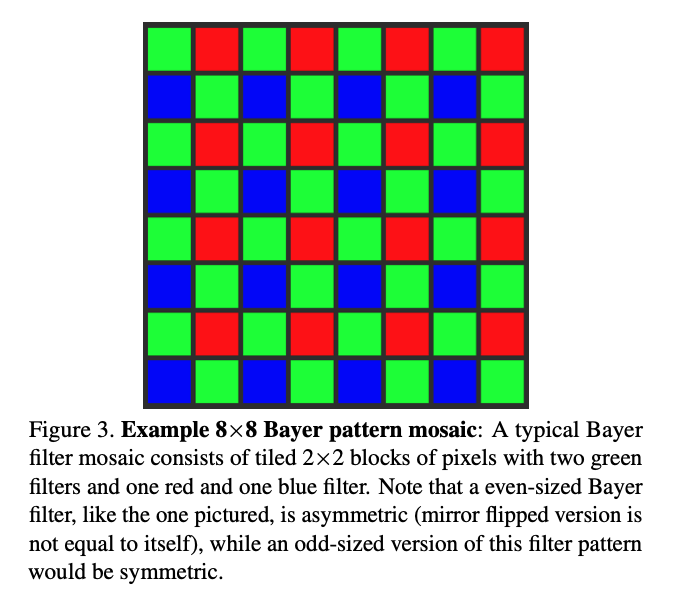
JPEG压缩算法(JPEG Compression):JPEG是一种有损的图像压缩方式,被广泛应用在如今大量的互联网图片上。一般以每16乘16的像素格为单位通过色彩空间变换,缩减像素采样,离散余弦变换等步骤来进行图片编码压缩。
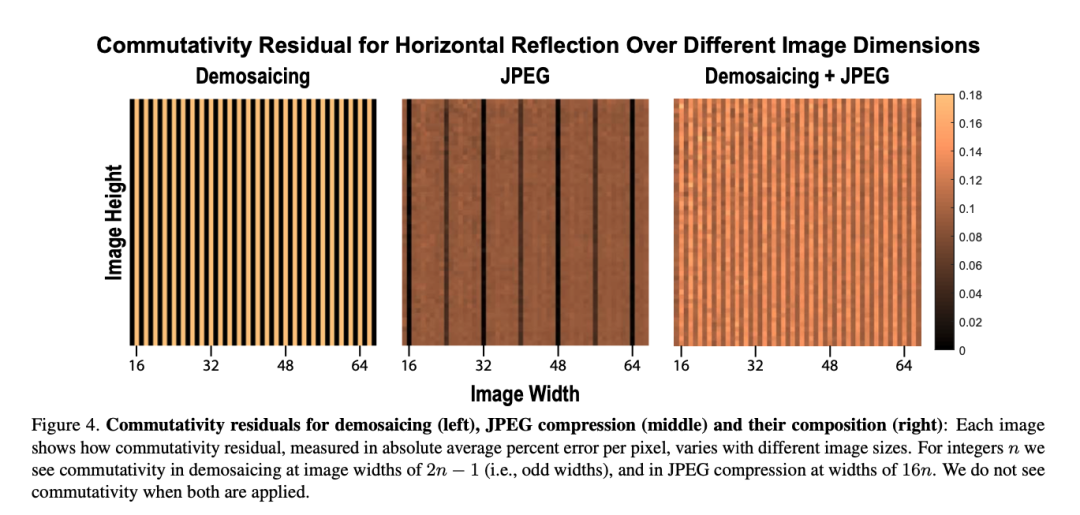
去马赛克或JPEG压缩算法单独使用时,会在特定的图片大小产生视觉手性现象。对于去马赛克,由于贝尔滤色镜为2乘2的像素格,且滤色镜本身不对称(参考上图绿红蓝绿的排序),任何能被2整除的图片宽度均会导致视觉手性。对于JPEG压缩,任何不被16整除的图片宽度均会导致视觉手性。这意味着,当去马赛克和JPEG压缩被共同使用时,任意宽度的图片都将产生视觉手性,因为同时满足不被2整除和能被16整除的数字不存在。 当使用随机剪裁(random cropping)时,去马赛克或JPEG压缩单独使用并不产生视觉手性现象。 当使用随机剪裁(random cropping)时,去马赛克和JPEG压缩同时使用将会产生视觉手性现象。这意味着互联网图片中可能存在大量有规律的,肉眼不可见的视觉手性线索,而人们将能够利用这类线索来进行图片识伪。

 也不具备视觉手性。
也不具备视觉手性。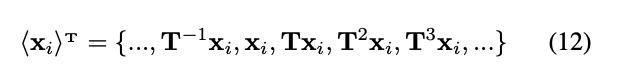
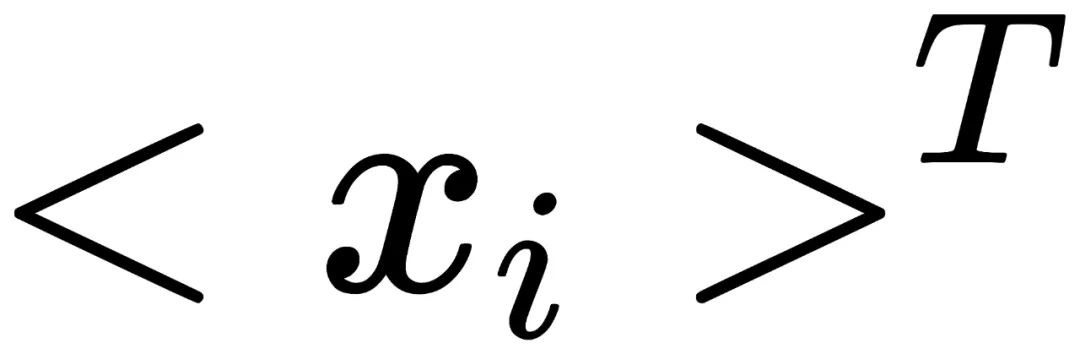 即为一个循环群,而这个循环群的单位元(identity element)可以选这个集合里面任意一个元素。这些循环群的群运算(group operation)可以被定义如下:
即为一个循环群,而这个循环群的单位元(identity element)可以选这个集合里面任意一个元素。这些循环群的群运算(group operation)可以被定义如下: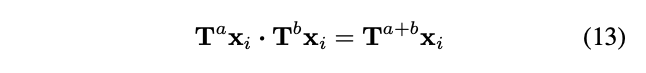
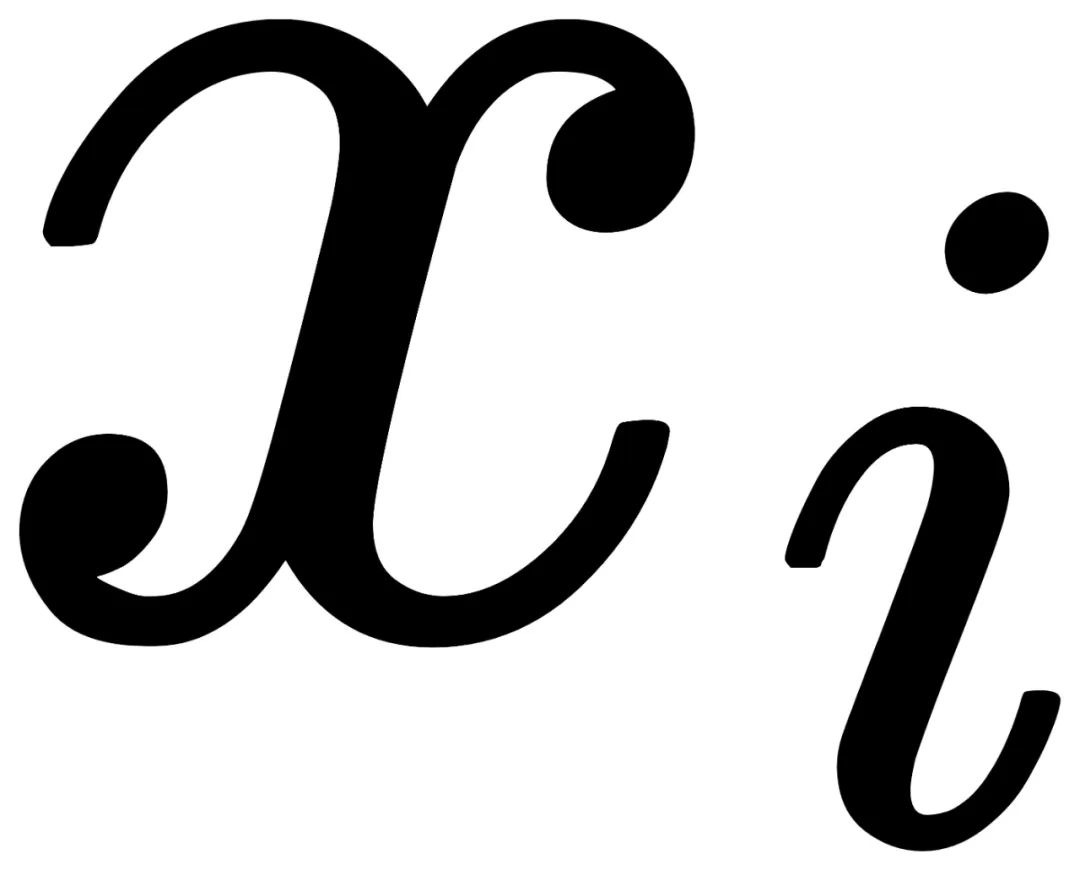 ,其所在群的阶为1
,其所在群的阶为1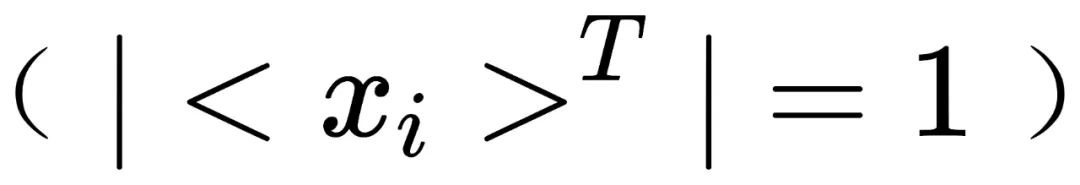 。对于不对称的一张照片
。对于不对称的一张照片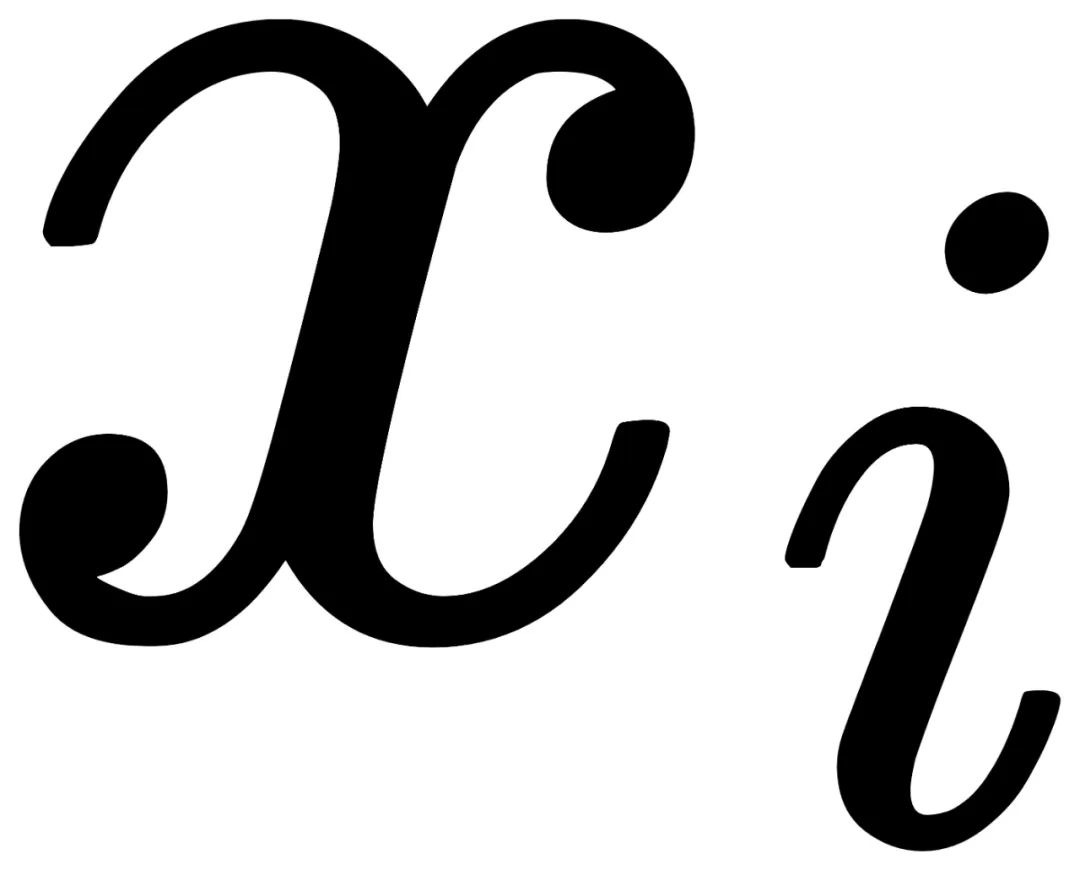 ,其所在群的阶为2
,其所在群的阶为2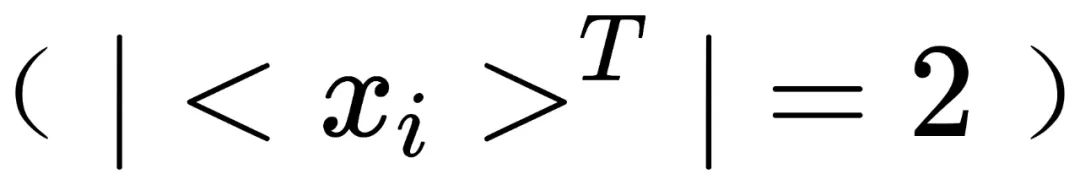 。
。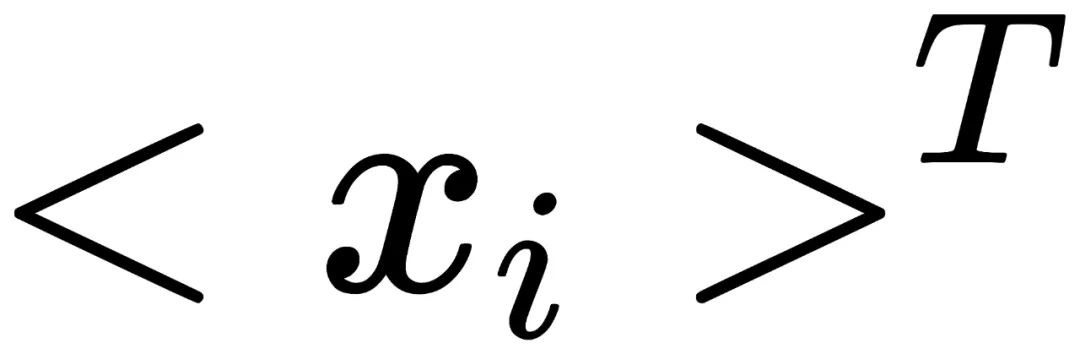 将变化为
将变化为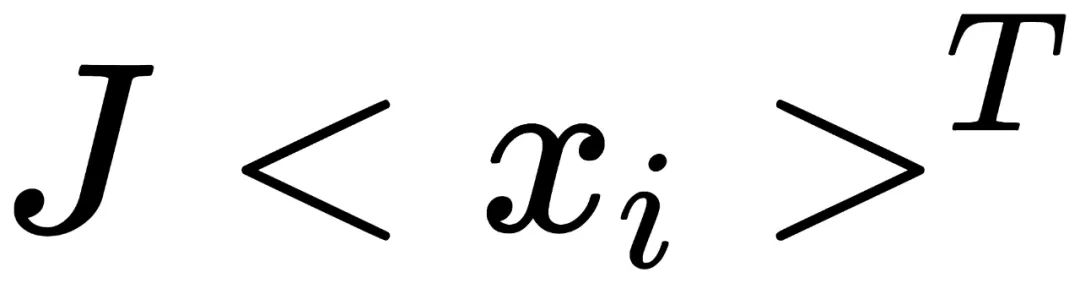 :
: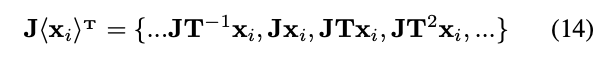
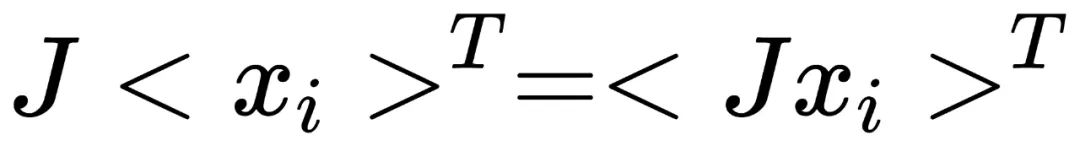 :
: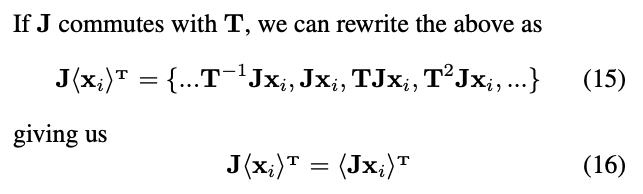
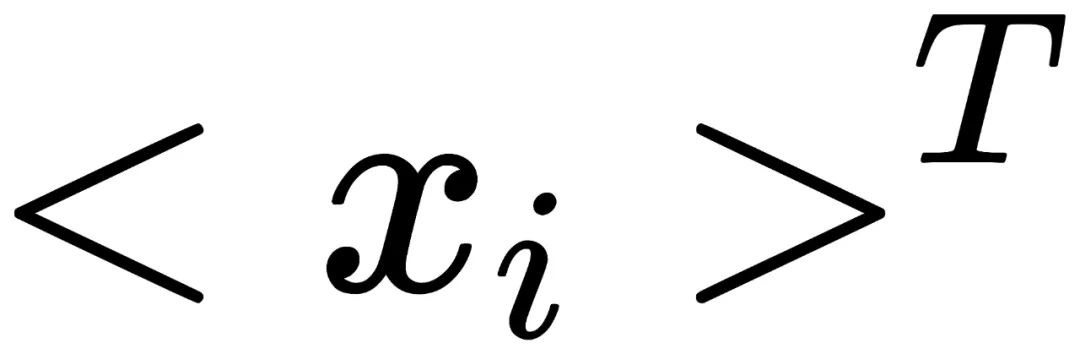 中的元素都有相同的概率出现。因此,由于经过J图像处理后循环群变为了
中的元素都有相同的概率出现。因此,由于经过J图像处理后循环群变为了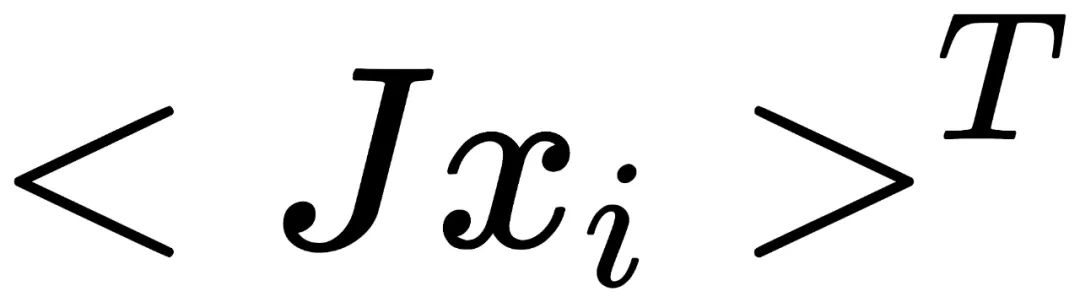 ,我们只需要证明以下运算为同态(homomorphism):
,我们只需要证明以下运算为同态(homomorphism):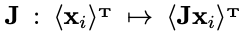
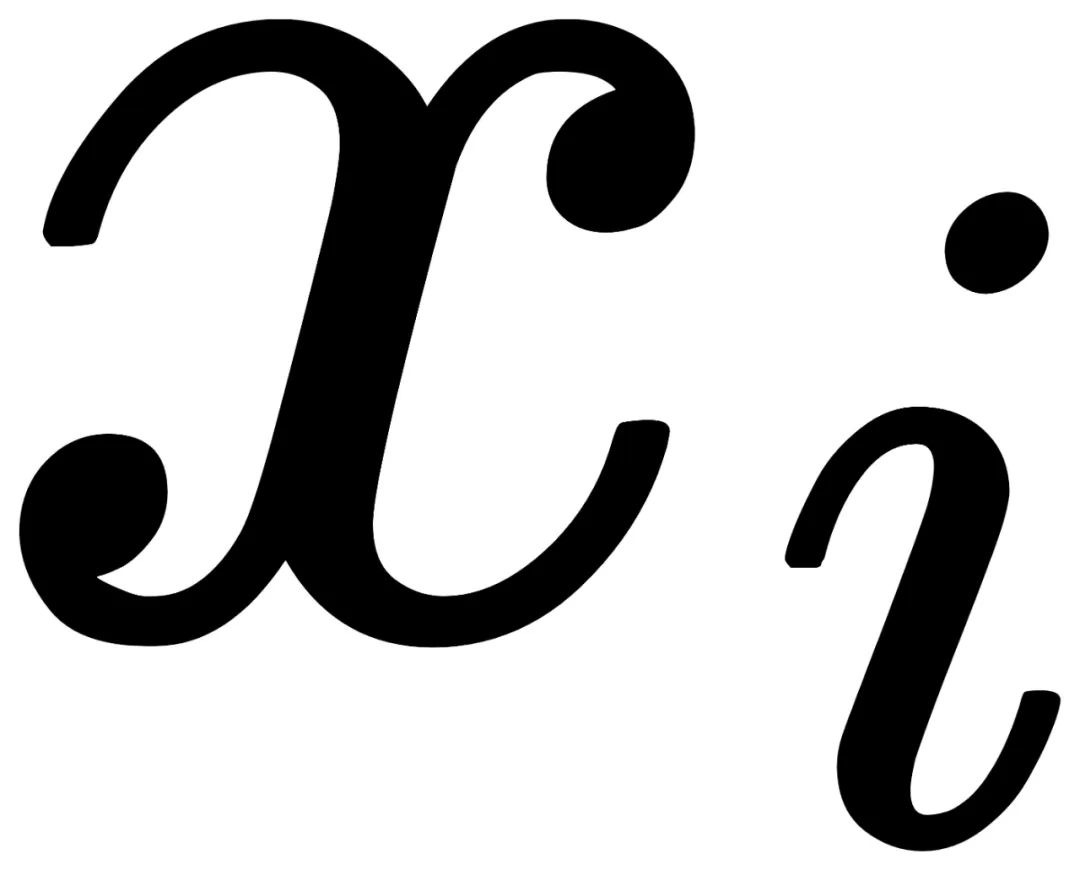 在原分布D上有着相同的概率,意味着每个输出
在原分布D上有着相同的概率,意味着每个输出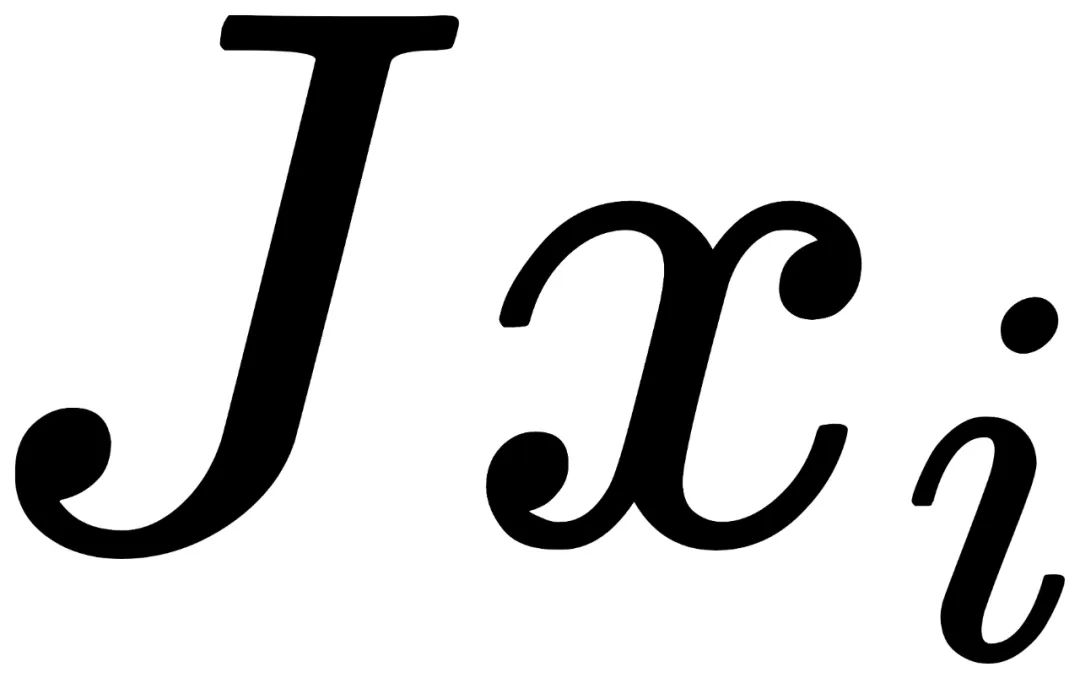 也具备相同的概率,也意味着
也具备相同的概率,也意味着 不具备视觉手性。
不具备视觉手性。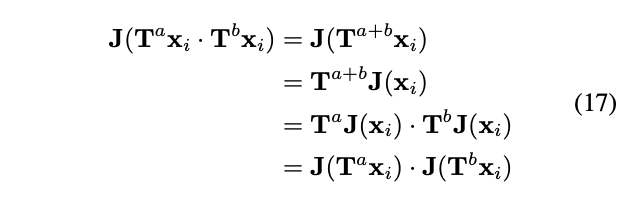
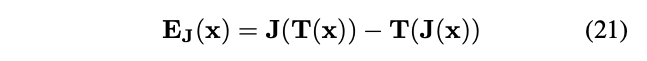

 是向右平移一格并剪裁,
是向右平移一格并剪裁, 是向右平移两个并剪裁)的结合,每一种有相同概率出现。
是向右平移两个并剪裁)的结合,每一种有相同概率出现。 ,
, ,
, ),而他们分别与T具备交换律时,我们可以用以下公式表达新的图像分布:
),而他们分别与T具备交换律时,我们可以用以下公式表达新的图像分布: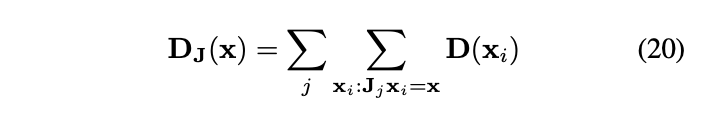

 ,
, ,
, )单独并不和T具备交换律,但在一种打乱的排列下具备交换性,如图中不同颜色的箭头所示。这种排列带来的交换律的关系可以用以下公式表达(a和b为排列中的序号)。
)单独并不和T具备交换律,但在一种打乱的排列下具备交换性,如图中不同颜色的箭头所示。这种排列带来的交换律的关系可以用以下公式表达(a和b为排列中的序号)。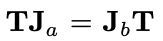
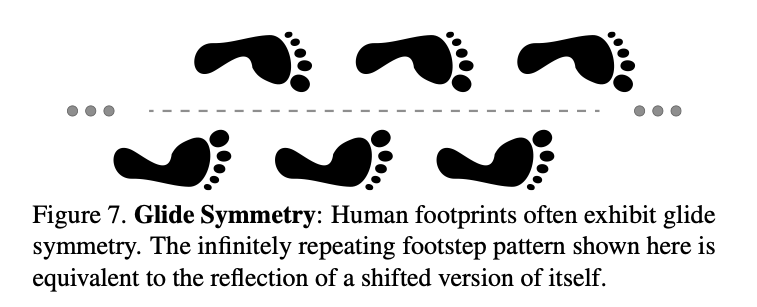

首先将任意图片x进行填充,并确保边缘足够大。 将填充后的图片进行Φ平移。 通过先后运算T和J,得到两种图片: 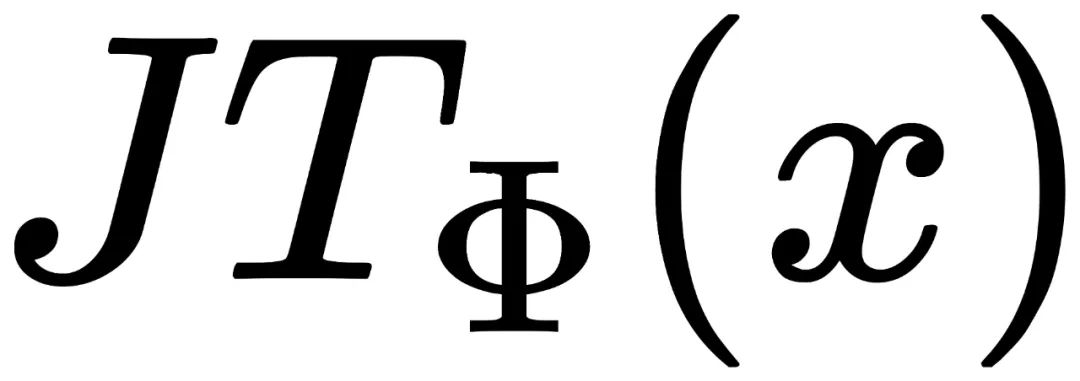 和
和 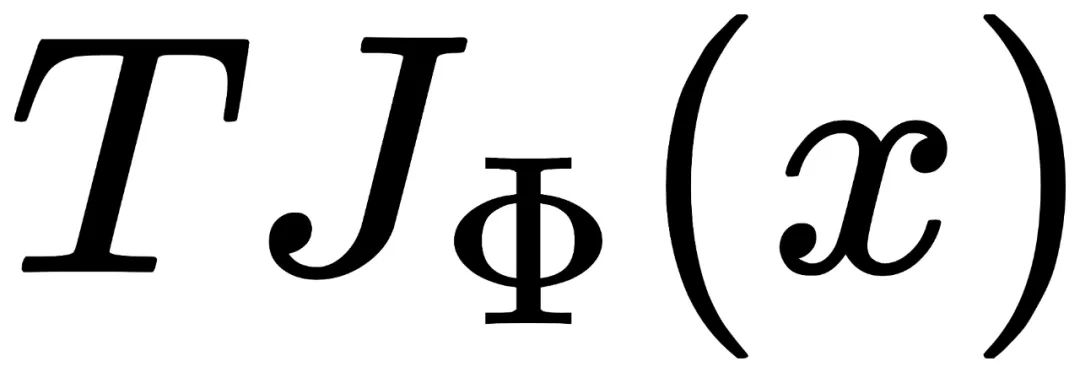
将这两个图片用T(-Φ)平移回原处。 将这两个图片多余的填充像素剪裁掉。
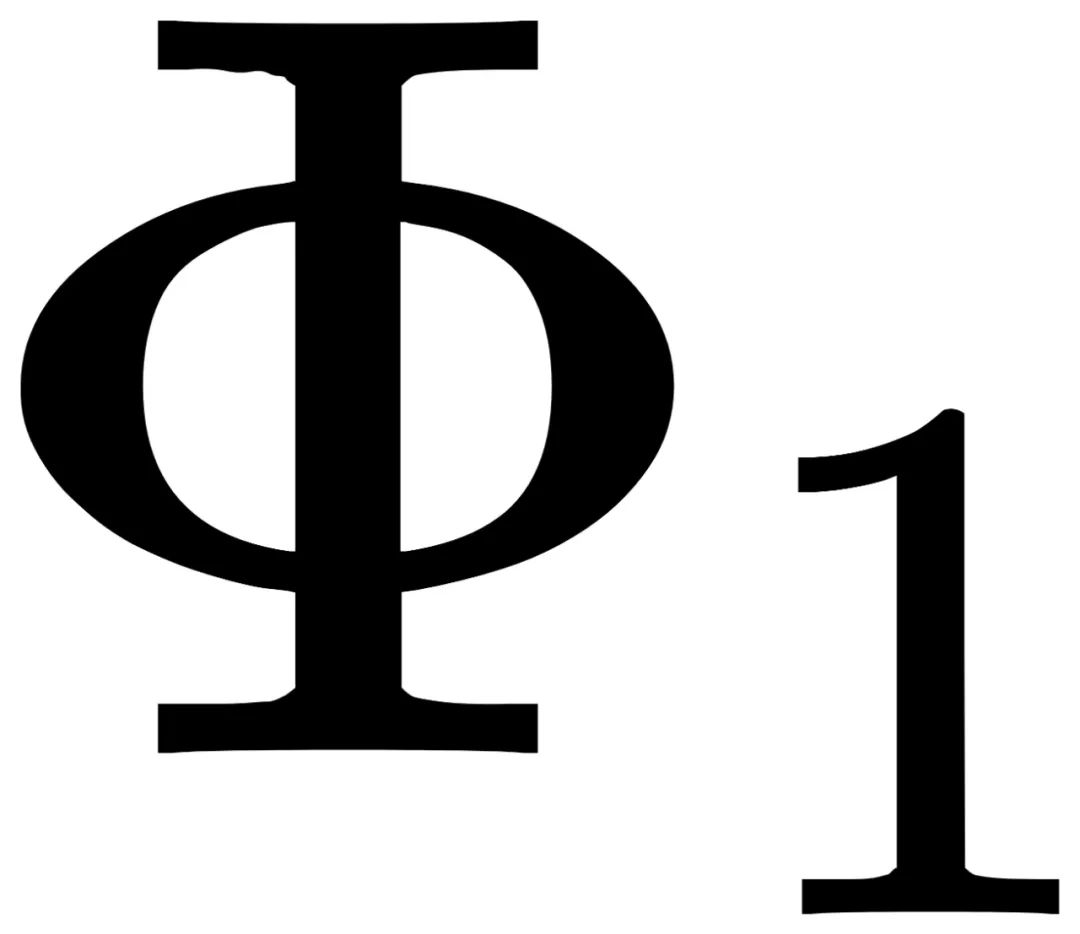 和
和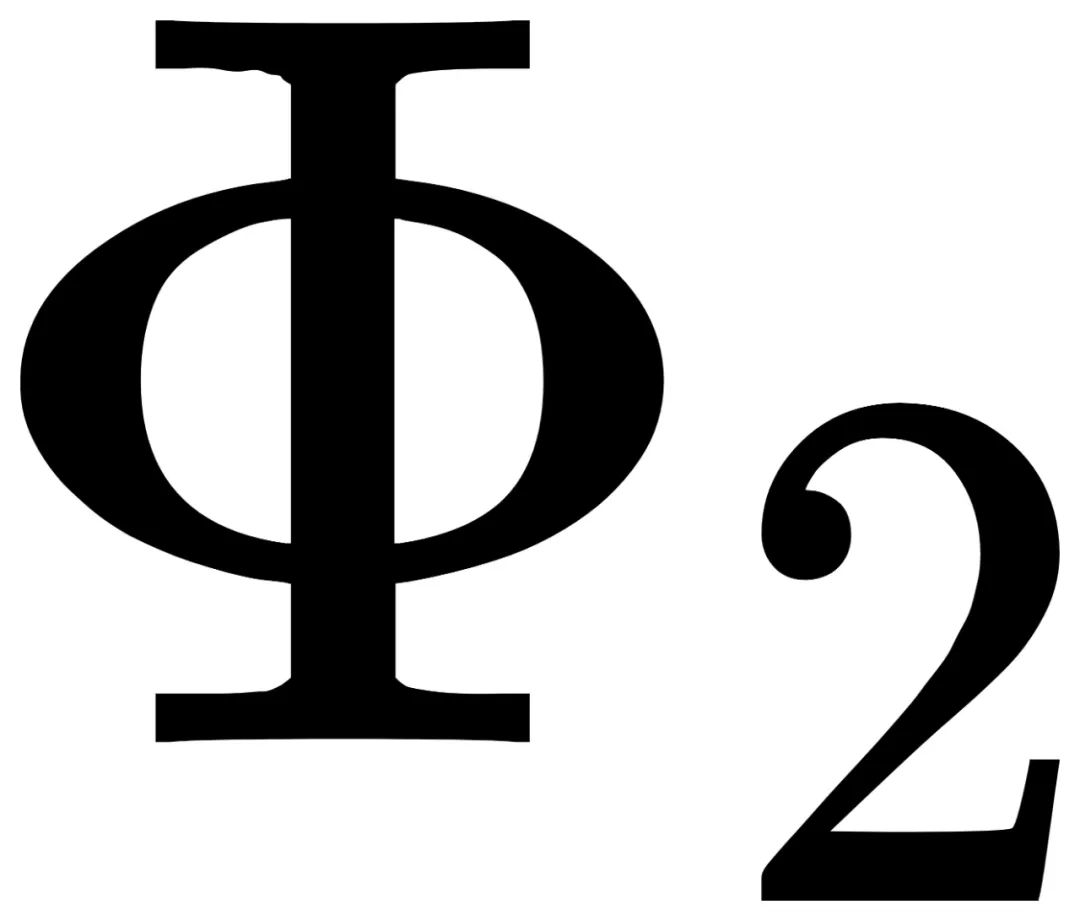 )检查以下残差是否为0:
)检查以下残差是否为0: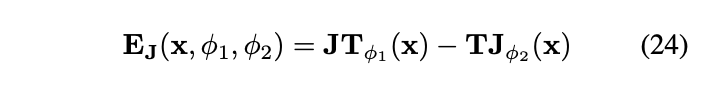
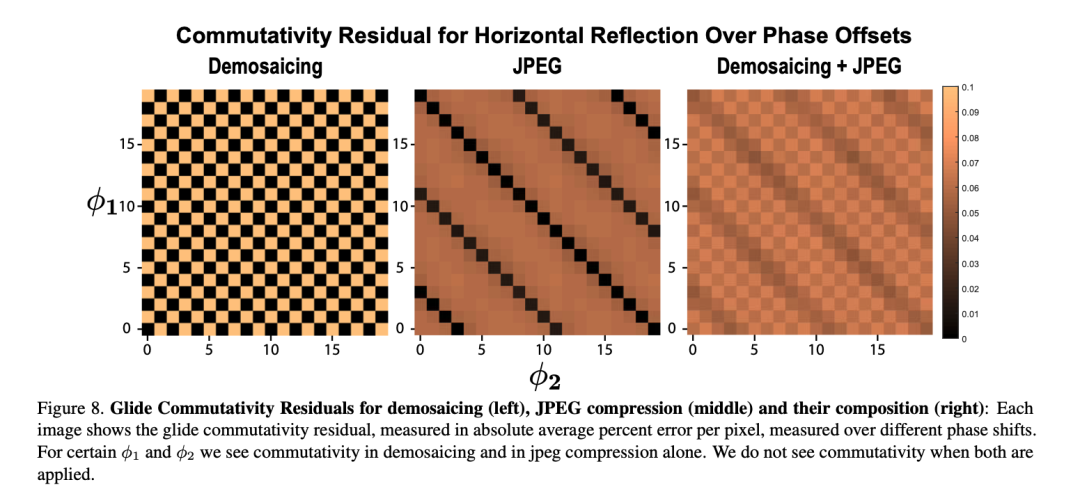
---END--- 重磅!码农突围-技术交流群已成立 扫码可添加码农突围助手,可申请加入码农突围大群和细分方向群,细分方向已涵盖:Java、Python、机器学习、大数据、人工智能等群。 一定要备注:开发方向+地点+学校/公司+昵称(如Java开发+上海+拼夕夕+猴子),根据格式备注,可更快被通过且邀请进群 ▲长按加群 推荐阅读
• 我在谷歌,女友在亚马逊,晒出2人总收入,网友:好酸 • 为什么建议大家使用 Linux 开发?爽(外加七个感叹号) • 华科女博士年薪156万入职华为!最新回应:在深圳也难买房… • Mysql,再见吧,select * ! • 他曾经复读才考上三本,如今让华为开出201万年薪(其实还拒绝了360万offer) • 痛惜!才29岁,年轻博士不幸离世 最近面试BAT,整理一份面试资料《Java面试BAT通关手册》,覆盖了Java核心技术、JVM、Java并发、SSM、微服务、数据库、数据结构等等。 获取方式:点“在看”,关注公众号并回复 BAT 领取,更多内容陆续奉上。 如有收获,点个在看,诚挚感谢 明天见(。・ω・。)ノ♡
评论
