在PyTorch中进行双线性采样：原理和代码详解-技术圈

↑ 点击蓝字关注极市平台

作者丨土豆@知乎

来源丨https://zhuanlan.zhihu.com/p/257958558

编辑丨极市平台

极市导读

本文记述了PyTorch中双线性插值和双线性采样操作的原理和代码，是一篇很清晰的笔记。>>加入极市CV技术交流群，走在计算机视觉的最前沿

在pytorch中的双线性采样（Bilinear Sample）

FesianXu 2020/09/16 at UESTC

前言

双线性插值与双线性采样是在图像插值和采样过程中常用的操作，在pytorch中对应的函数是torch.nn.functional.grid_sample，本文对该操作的原理和代码例程进行笔记。如有谬误，请联系指正，转载请联系作者并注明出处，谢谢。

E-mail: FesianXu@gmail.com

QQ: 973926198

GitHub: https://github.com/FesianXu

知乎专栏: https://zhuanlan.zhihu.com/c_1265262560611299328

双线性插值原理

插值（interpolation）在数学上指的是 一种估计方法，其根据已知的离散数据点去构造新的数据点。以曲线插值为例子，如Fig 1.1所示的曲线线性插值为例，其中红色数据点是已知的数据点，而蓝色线是根据相邻的两个红色数据点进行线性插值估计出来的。

Fig 1.1 一个简单的曲线线性插值的例子

一维的曲线插值的原理可以推广到任意维度的数据形式上，比如我们常见的图像是一种二维数据，就可以进行二维插值，常见的插值方法如Fig 1.2所示。

Fig 1.2 常见的1D和2D数据插值方法

在本文中，我们主要讨论的是双线性采样，而双线性采样和双线性插值紧密相关，因此本章节主要介绍双线性插值。还是以2D图像插值为例子，如Fig 1.3所示，假设图片上给定了红色数据点的像素值，假设待求的绿色点，其中已知每个顶点像素坐标为：

而每个顶点的像素值表示为。通过简单的线性插值（按比例划分），我们可以求出蓝色数据点的估计值：

然后通过蓝色点，再一次进行线性插值，可以估计出绿色点的值：

因为该方法涉及到了两轮（注意不是两次，而是三次）的线性插值，因此称之为双线性插值（Bilinear Interpolation）。

Fig 1.3 给定了四个红色数据点（像素点）的值，通过双线性插值求中间的绿色数据点的值

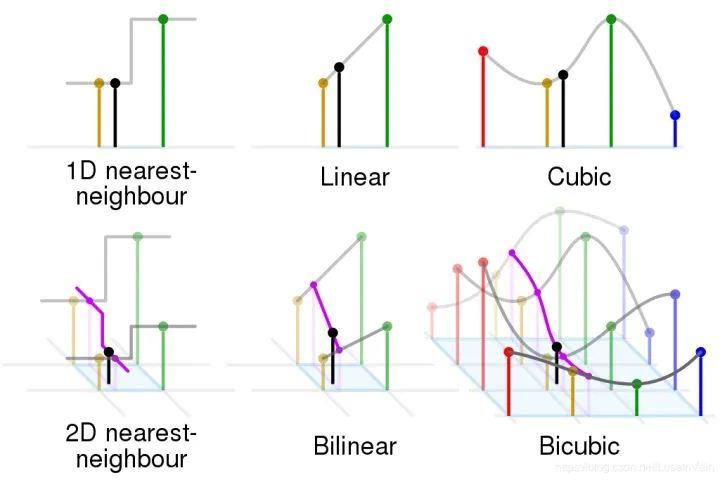
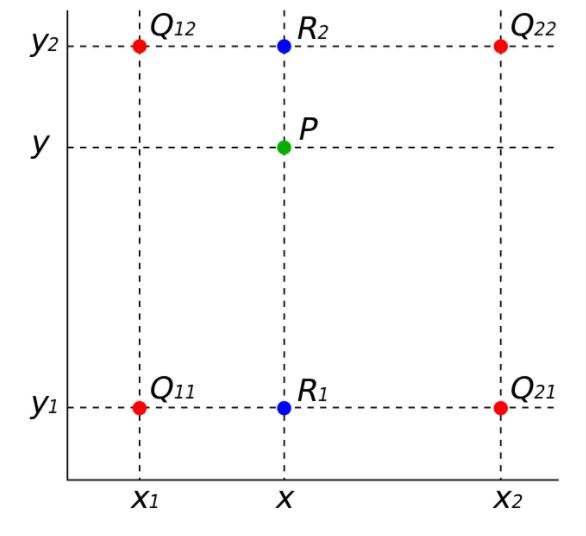
双线性采样以及grid_sample

在深度学习框架pytorch中提供了一种称之为双线性采样（Bilinear Sample）的函数torch.nn.functional.grid_sample [1]，该函数主要输入一个形状为的input张量，输入一个形状为的grid张量，输出一个形状为的output张量。

其中为batch批次，我们主要关注后面的维度的代表意义。输入的grid是一个大小的空间位置矩阵，其中每个元素都代表着一个二维空间坐标，该坐标指明了在input上采样的坐标，而输出张量的每个位置output[n,:,h,w]的值，取决于这个输入input和采样坐标的值（通过双线性插值形成）。通过这个函数，可以通过指定原图的不同坐标位置，实现图片的变形（deformation）等，在很多研究中有着广泛地应用[2]。

注意到这里的输出张量尺寸和输入张量尺寸是不一定一致的，因此涉及到了插值过程，而且输入的grid的每一个坐标都是归一化到了之间的，我们举一个简单的代码例子，明晰下细节。

import torch.nn.functional as F
import torch
inputv = torch.arange(4*4).view(1, 1, 4, 4).float()
print(inputv)
'''
输出尺寸为(1,1,4,4)
输出为：tensor([[[[ 0.,  1.,  2.,  3.],
          [ 4.,  5.,  6.,  7.],
          [ 8.,  9., 10., 11.],
          [12., 13., 14., 15.]]]])
'''
# 生成grid，这个grid大小为(1,8,8,2)，空间尺寸而言是原输入图片的两倍。
d = torch.linspace(-1,1, 8)
meshx, meshy = torch.meshgrid((d, d))
grid = torch.stack((meshy, meshx), 2)
grid = grid.unsqueeze(0) # add batch dim

# 进行双线性采样，其中指定align_corners=True保证了输出的整个图片的角边像素与原输入的一致性。
output = F.grid_sample(inputv, grid,align_corners=True)
print(output)
'''
tensor([[[[ 0.0000,  0.4286,  0.8571,  1.2857,  1.7143,  2.1429,  2.5714,
            3.0000],
          [ 1.7143,  2.1429,  2.5714,  3.0000,  3.4286,  3.8571,  4.2857,
            4.7143],
          [ 3.4286,  3.8571,  4.2857,  4.7143,  5.1429,  5.5714,  6.0000,
            6.4286],
          [ 5.1429,  5.5714,  6.0000,  6.4286,  6.8571,  7.2857,  7.7143,
            8.1429],
          [ 6.8571,  7.2857,  7.7143,  8.1429,  8.5714,  9.0000,  9.4286,
            9.8571],
          [ 8.5714,  9.0000,  9.4286,  9.8571, 10.2857, 10.7143, 11.1429,
           11.5714],
          [10.2857, 10.7143, 11.1429, 11.5714, 12.0000, 12.4286, 12.8571,
           13.2857],
          [12.0000, 12.4286, 12.8571, 13.2857, 13.7143, 14.1429, 14.5714,
           15.0000]]]])
'''

在这个过程中，我们生成的采样坐标网格grid很简单，单纯只是在x,y两个维度，都把均分为了8份。

我们分析下双线性采样后的每个像素的大小计算过程。因为每个输入坐标都是，而实际原输入的矩阵大小为，而且刚好是一个方阵，因此可以计算出从grid到实际坐标的映射为:

这个映射将归一化坐标映射到了实际的原图坐标，如果不是方阵，那么就必须对每个维度都计算一个映射方程。

我们暂时只考虑怎么计算其中某一个像素的值，暂时我们考虑grid坐标为的值。我们打印出grid[0,1,1,:]，发现这个归一化坐标值为tensor([[-0.7143, -0.7143]])，那么通过反归一化映射，也就是式子(1)后，有实际图片坐标为，这个时候我们发现这个坐标不是整数，因此为了求出这个坐标的像素值，我们要通过之前谈到的双线性插值去估计。

首先求出每一行的插值结果，有，这个是在中插值的结果；有这个是在范围内插值的结果，然后再在中进行插值，有。这就是整个双线性采样的计算过程。

注意：这个输入input也可以是的5D输入，该输入考虑的是对视频进行处理。本文中只考虑了图片数据，不过原理是类似的，不再赘述。

Reference

[1]. https://pytorch.org/docs/stable/nn.functional.html#torch.nn.functional.grid_sample

[2]. https://blog.csdn.net/LoseInVain/article/details/108710063

推荐阅读

基于Pytorch的动态卷积复现
综述｜核心开发者全面解读Pytorch内部机制
PyTorch扩展自定义PyThon/C++(CUDA)算子的若干方法总结

添加极市小助手微信（ID : cvmart2），备注：姓名-学校/公司-研究方向-城市（如：小极-北大-目标检测-深圳），即可申请加入极市目标检测/图像分割/工业检测/人脸/医学影像/3D/SLAM/自动驾驶/超分辨率/姿态估计/ReID/GAN/图像增强/OCR/视频理解等技术交流群：每月大咖直播分享、真实项目需求对接、求职内推、算法竞赛、干货资讯汇总、与 10000+来自港科大、北大、清华、中科院、CMU、腾讯、百度等名校名企视觉开发者互动交流~

△长按添加极市小助手

△长按关注极市平台，获取最新CV干货

觉得有用麻烦给个在看啦~