【机器学习】从一个风控案例讲起-古老而经典的朴素贝叶斯
今天给大家带来的文章,关于朴素贝叶斯的,一个古老而经典的算法,充分的理解有利于对风控特征或者识别的开拓新的思路。
一、从一个案例讲起



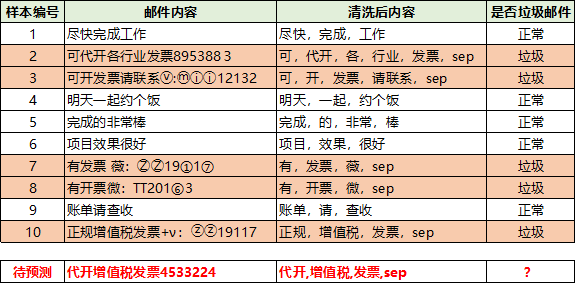
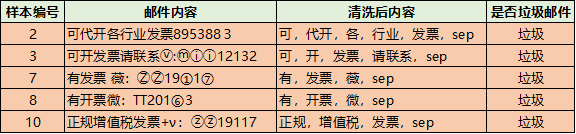
data = ['尽快,完成,工作','可,代开,各,行业,发票,sep','可,开,发票,请联系,sep','明天,一起,约个饭','完成,的,非常,棒','项目,效果,很好','有,发票,薇,sep','有,开票,微,sep','账单,请,查收','正规,增值税,发票,sep']label=[0,1,1,0,0,0,1,1,0,1]vectorizer_word = TfidfVectorizer()vectorizer_word.fit(data,)#vectorizer_word.vocabulary_train = vectorizer_word.transform(data)test = vectorizer_word.transform(['代开,增值税,发票,sep'])from sklearn.naive_bayesimport BernoulliNBclf = BernoulliNB()clf.fit(train.toarray(), label)clf.predict(test.toarray(),)clf.predict_proba(test.toarray(),)array([[0.00154805, 0.99845195]])算出来的概率也是0.99845195左右,和我们手动计算的差不多
二、贝叶斯定理概述
贝叶斯定理由英国数学家贝叶斯 ( Thomas Bayes 1702-1761 ) 发展,用来描述两个条件概率之间的关系,比如 P(A|B) 和 P(B|A)。主要用于文本分类。朴素贝叶斯法是基于贝叶斯定理与特征条件独立假设的分类方法。贝叶斯定理太有用了,不管是在投资领域,还是机器学习,或是日常生活中高手几乎都在用到它。

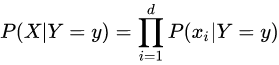

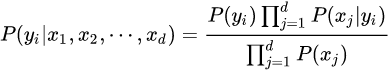

三、零概率问题连乘操作

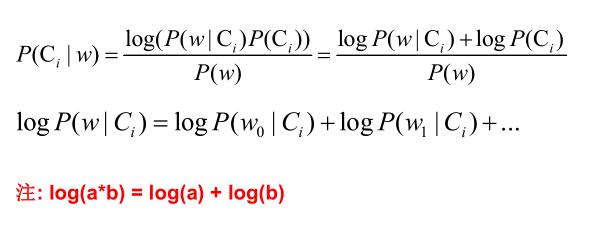
四、连续型变量概率计算
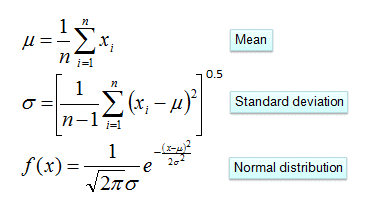
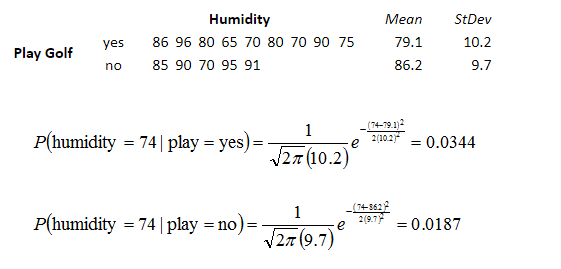
五、Python库中的贝叶斯
GaussianNB
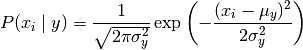
MultinomialNB
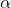 。
。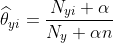
ComplementNB

BernoulliNB

CategoricalNB


案例测试from sklearn.naive_bayes import MultinomialNB,GaussianNB,BernoulliNB,ComplementNBfrom sklearn.datasets import load_breast_cancerfrom sklearn.model_selection import cross_val_scoreX,y = load_breast_cancer().data,load_breast_cancer().targetnb1= GaussianNB()nb2= MultinomialNB()nb3= BernoulliNB()nb4= ComplementNB()for model in [nb1,nb2,nb3,nb4]:scores=cross_val_score(model,X,y,cv=10,scoring='accuracy')print("Accuracy:{:.4f}".format(scores.mean()))Accuracy:0.9368Accuracy:0.8928Accuracy:0.6274Accuracy:0.8928from sklearn.naive_bayes import MultinomialNB,GaussianNB,BernoulliNB,ComplementNB ,CategoricalNBfrom sklearn.datasets import load_irisfrom sklearn.model_selection import cross_val_scoreX,y = load_iris().data,load_iris().targetgn1 = GaussianNB()gn2 = MultinomialNB()gn3 = BernoulliNB()gn4 = ComplementNB()gn5 = CategoricalNB(alpha=1)for model in [gn1,gn2,gn3,gn4,gn5]:scores = cross_val_score(model,X,y,cv=10,scoring='accuracy')print("Accuracy:{:.4f}".format(scores.mean()))Accuracy:0.9533Accuracy:0.9533Accuracy:0.3333Accuracy:0.6667Accuracy:0.9267
from sklearn import preprocessingenc = preprocessing.OneHotEncoder() # 创建对象from sklearn.datasets import load_irisX,y = load_iris().data,load_iris().targetenc.fit(X)array = enc.transform(X).toarray()from sklearn.naive_bayes import MultinomialNB,GaussianNB,BernoulliNB,ComplementNB ,CategoricalNBfrom sklearn.datasets import load_irisfrom sklearn.model_selection import cross_val_scoreX,y = load_iris().data,load_iris().targetgn1 = GaussianNB()gn2 = MultinomialNB()gn3 = BernoulliNB()gn4 = ComplementNB()for model in [gn1,gn2,gn3,gn4]:scores=cross_val_score(model,array,y,cv=10,scoring='accuracy')print("Accuracy:{:.4f}".format(scores.mean()))Accuracy:0.8933Accuracy:0.9333Accuracy:0.9333Accuracy:0.9400往期精彩回顾
适合初学者入门人工智能的路线及资料下载 (图文+视频)机器学习入门系列下载 中国大学慕课《机器学习》(黄海广主讲) 机器学习及深度学习笔记等资料打印 《统计学习方法》的代码复现专辑 AI基础下载 机器学习交流qq群955171419,加入微信群请扫码:
评论
