风控ML[19] | 风控建模中的LR模型为什么出场率这么高?-技术圈

00 Index

01 LR是什么？
02 LR在金融领域有哪些优势
03 LR的算法推导过程
04 LR的重要参数
05 LR与评分卡
06 总结一下

🙊 01 LR是什么？

LR全称是 Logistic Regression，中文名为逻辑回归模型。虽然名字里带有“回归”二字，但其实是属于分类模型，属于线性分类器。既然LR里有“回归”，那就说明了它和回归多少有些渊源了。我们知道线性回归模型的一般表达形式如下：

θθθθ

我们还可以用矩阵来表示上面这个方程：

其中，θ_0被我们称为截距（intercept），其余的θ被称为系数（coefficient）。而我们知道，线性回归模型的输出值是连续型，如果要将其映射成0和1的二分类值的话，就需要引入 Link Function，也就是我们常说的 Sigmoid函数：

它是一个S型的曲线函数，当z趋向于正无穷，它趋向于1，而z趋向于负无穷，它趋向于0，所以它可以让预测结果都映射到0-1之间，有点像归一化。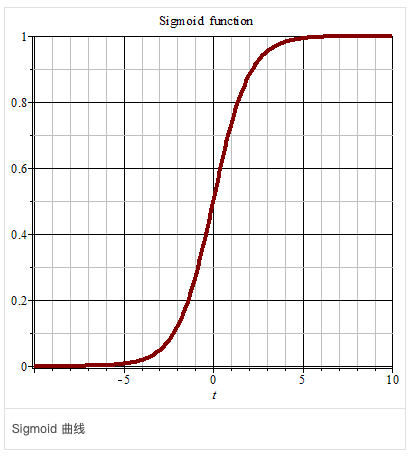我们把线性回归的θ代入到Sigmoid函数中，可以得到逻辑回归的一般表现形式：

如果我们对二元逻辑回归取odds（形似几率，），其实是可以得到线性回归的，不信？请看：

θ θ θ

所以其实我们的核心工作就是求解z中的θ，让其可以拟合数据得到相对准确的预测结果。

🏆 02 LR在金融领域有哪些优势

这个问题其实一个很重要的优势就是可解释性，当然，还有好几点：

可以解释性好：LR模型概率输出可以转化为对应的二分类概率，具备良好的可解释性，这对于金融行业而言非常重要，可以帮助业务人员更好理解模型以及模型内部的逻辑。
算法简单快速：LR算法是一种简单快速的模型，数据量大的情况下可以一定程度上减轻计算压力，大大提高了模型计算效率。
适用范围广：LR模型可以应用于多种金融风险预测，如信用风险、违约风险、欺诈风险等等，具有良好的适用性。
模型稳定性好：LR模型在面对缺失值、异常值、过拟合等常见问题时表现得比较稳定，可以有效应对金融领域多种异常情况。

综上所述，LR算法在金融领域中得到广泛应用，依托于其解释性好、算法简单快速、适用范围广和模型稳定性好等优点。但是，LR模型也存在一些缺点：

不能处理非线性关系：LR模型只能处理线性关系，对于非线性关系无法很好地进行建模。
劣化快：当自变量与因变量之间的关系非常复杂时，LR模型的表现可能会迅速劣化。
非常依赖数据质量：LR模型对数据质量要求比较高，如果数据存在较多噪声或缺失值等问题，模型的表现可能会受到严重影响。

因此，需要根据具体情况综合考虑LR模型的优劣，并在合适的场景下进行应用。

✍️ 03 LR的算法推导过程

我会简单易懂地介绍一下逻辑回归的推导过程。逻辑回归是一种二分类算法，它的目标是学习一个适当的模型，能够预测一个特定的输入属于哪一类。

首先，我们需要用线性回归模型来表示预测结果：

其中，代表预测结果，是权重系数，是输入特征，是偏移量（也称为截距）。

但是，线性回归模型的输出值是一个连续变量，不能直接用于二分类问题的输出。这时，我们需要引入一个sigmoid函数将线性回归模型的输出值映射到[0,1]之间。

sigmoid函数的定义如下：

其中，z表示线性回归模型的输出值（即）。

sigmoid函数经过变换，可得到输出值的概率表示：

这里，表示对于给定的输入特征，预测结果为1的概率，表示预测结果为0的概率。

接着，我们需要定义一个目标函数来评估模型的预测能力。通常，我们采用最大似然估计来求解权重系数和偏移量（即和）。

具体而言，我们可以构建一个似然函数L来表示给定样本集合下模型产生预测结果的概率：

其中，表示每个样本真实的标签。

为了简化目标函数的计算，我们可以对似然函数L取对数，得到对数似然函数：

最终，我们的目标是求解使对数似然函数ln(L)最大的权重系数w和偏移量b，一般采用梯度下降法来求解。

⚠️ 04 LR的重要参数

逻辑回归（LR）模型的重要参数包括以下几点：

正则化参数（Regularization Parameter）：用于控制模型的复杂度，并防止过拟合。常见的正则化方法有 L1 正则化和 L2 正则化。
学习率（Learning Rate）：梯度下降算法中每次迭代更新参数时的步长大小。如果学习率过大，可能导致无法收敛；如果学习率过小，则会使得算法收敛速度缓慢。
最大迭代次数（Maximum Iterations）：指定最大的迭代次数，如果达到了最大迭代次数仍未收敛，则停止训练。
收敛阈值（Tolerance）：用于判断算法是否已经收敛，当两次迭代之间的代价函数改变量小于收敛阈值时，认为算法已经收敛。
求解器（Solver）：LR 模型在求解参数时可以使用不同的求解器，例如梯度下降、牛顿法等。不同的求解器对于不同的数据集和问题有着不同的表现。
类别权重（Class Weight）：如果分类问题中正负样本的比例非常失衡，我们可以通过类别权重来平衡样本，以便更好地学习到少数类别的特征。通常情况下，将少数类别的样本赋予更高的权重。

对于这些重要参数，可以通过以下方式进行调参：

交叉验证：使用交叉验证技术对模型参数进行调整，可以得到更可靠的模型效果。
网格搜索：使用网格搜索技术对模型参数进行调整，选取不同的参数组合进行模型训练和评估，以找到最优解。
随机搜索：使用随机搜索技术对模型参数进行调整，随机选取一些参数组合进行训练和评估，以找到最优解。
经验法则：根据经验法则对模型参数进行调整，如对学习率进行指数级别的递减。

通过以上方法，可以对LR模型的重要参数进行调参，以达到最优的模型效果。

🧾 05 LR与评分卡

评分卡（Scorecard）是一种广泛应用于信用风险评估、反欺诈等领域的规则集合，用于对个人或企业进行风险评估，并根据评分结果进行决策。

在使用 LR 模型构建评分卡时，通常需要进行如下步骤：

数据预处理：包括数据清洗、缺失值处理、异常值处理等。
特征工程：选择和构造能够区分好坏客户的特征变量，例如借款人的年龄、收入、负债情况等。
模型训练：将选定的特征变量输入到 LR 模型中进行训练，得到模型参数。
计算分数：使用模型参数和特征变量计算评分卡上的得分，通常可以采用 WOE（Weight of Evidence）编码的方式将连续变量离散化，并使用 IV（Information Value）来评估特征的重要性。
设计评分卡：将得分映射到对应的评分类别上，例如将得分划分为 A \B\C\D\E\F 等级别。
模型验证与维护：对模型进行验证和监控，确保模型的准确性和稳定性，并及时更新评分卡以适应新的业务需求和环境变化。

🤔假如已经完成了LR的建模工作，那么要怎么输出评分卡，给到业务部门使用？

具体可以按下面步骤来走：将模型参数导出：将训练得到的 LR 模型参数导出为 Excel 或 CSV 格式，以便业务部门方便查看。

计算基础分值：在评分卡中，通常会设定一个基础分值，用来表示最优客户的得分。基础分值可以根据历史数据或领域专家的判断进行设定，一般情况下在 400 到 600 分之间。
计算评分卡得分：将 LR 模型参数和特征变量的 WOE 编码对应起来，并根据 IV 值来选择重要的特征变量，然后结合基础分值计算每个客户的评分卡得分。具体计算方法为：将所有特征的 WOE 值乘以其对应的回归系数，再将结果相加，最后加上基础分值即可。关于WOE和IV的原理和计算公式，可以参考之前写的一篇文章：《风控ML[3] | 风控建模的WOE与IV》
制作评分卡表格：将计算得到的评分卡得分制作成表格，并说明不同得分区间所对应的等级、风险等级等信息。可以使用 Excel 或 PPT 等工具进行制作。
发布评分卡：将评分卡表格以邮件、文档等形式发送给业务部门，并提供必要的说明和培训，确保他们能够正确理解和使用评分卡。

✍️下面举一个案例：

假设你正在为一家银行建立贷款违约风险评估模型，数据集包含了客户的个人信息、信用历史等多个变量。经过数据预处理和特征工程后，你使用逻辑回归（Logistic Regression，LR）算法进行建模，并得到了如下的模型参数：

变量名称	回归系数
年龄	-0.12
收入	0.08
负债比例	0.15
历史违约	0.85

为了将 LR 模型转换为评分卡，你需要进行如下步骤：

计算基础分值：在这个例子中，我们假设最优客户的得分为 500 分。因此，基础分值可以设置为 500 分。
计算评分卡得分：根据 WOE 编码将连续变量离散化，并计算每个变量在不同分组下的 WOE 值。例如，对于年龄变量，可以将其分为四个区间，然后根据历史数据计算出每个区间的违约率和非违约率，进而计算出 WOE 值，如下表所示：

年龄区间	违约率	非违约率	WOE
<30	0.20	0.80	-0.60
30-40	0.10	0.90	-1.20
40-50	0.05	0.95	-1.70
>50	0.03	0.97	-2.10

然后将每个变量的 WOE 值乘以其对应的回归系数，并相加，再加上基础分值即可得到每个客户的评分卡得分。

制作评分卡表格：将计算得到的评分卡得分制作成表格，并说明不同得分区间所对应的等级、风险等级等信息。例如，可以将得分划分为 A\B\C\D等级别，如下表所示：

评分区间	得分范围	等级	风险等级
700-850	>= 700	A	低
650-699	650-699	B	中
600-649	600-649	C	高
<600	< 600	D	极高

发布评分卡：将评分卡表格以邮件、文档等形式发送给业务部门，并提供必要的说明和培训，确保他们能够正确理解和使用评分卡。

以上是一个简单的评分卡制作示例，实际情况可能更加复杂。需要注意的是，在实际应用中需要根据具体业务场景和实践经验进行调整和优化，同时进行模型的验证和更新以保持模型的准确性和稳定性。

📖 06 总结一下

逻辑回归（Logistic Regression，LR）在金融领域有广泛应用，可以用来进行信用评级、欺诈检测、客户流失预测等任务。以下是LR在金融领域的应用总结：

首先，LR被广泛应用于信用评级领域。通过建立一个逻辑回归模型，可以将不同客户的信用风险进行分类，为银行或其他金融机构提供决策依据。同时，LR还可以作为其他分类算法的基础模型，如决策树、支持向量机等。

其次，LR还可以用于欺诈检测任务。金融欺诈通常伴随着异常行为，如交易金额异常、地点异常等。通过建立一个LR模型，可以对这些异常行为进行分类，从而及时发现并防止金融欺诈事件的发生。

此外，LR还可以用于客户流失预测任务。在金融领域中，客户流失是一个重要的问题，因为吸引新客户比留住老客户更加困难。通过建立一个LR模型，可以预测某个客户是否会流失，从而针对性地采取措施，留住该客户并提高整体业绩。

总之，逻辑回归在金融领域具有广泛应用，可以帮助金融机构进行信用评级、欺诈检测、客户流失预测等任务。

广而

告之

PICK ME

朋友们，阿Sam这边也开通了小红书账号，也会定期发布一些机器学习、风控挖掘、特征工程等相关工程（几乎日更哦），欢迎大家也关注关注，哈哈～