漫画:有趣的 “切蛋糕“ 问题

导读:一道又烧脑又有趣的ACM比赛题目。







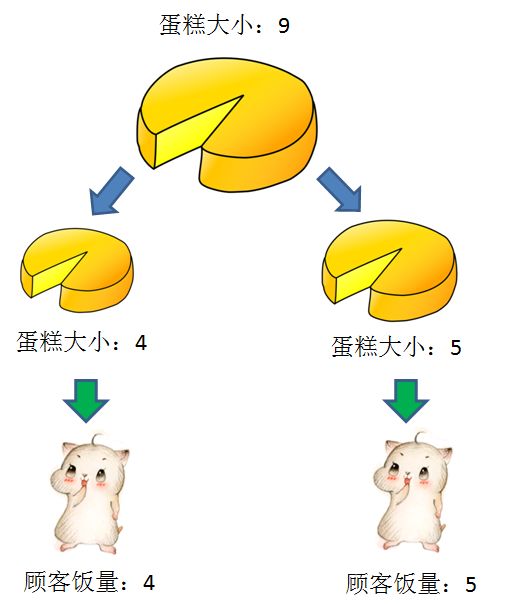
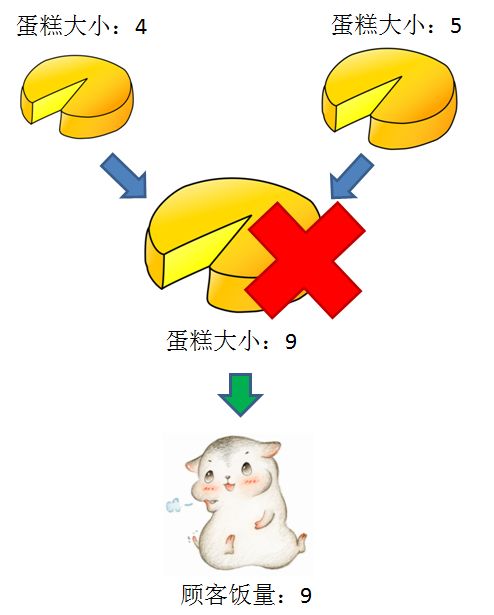
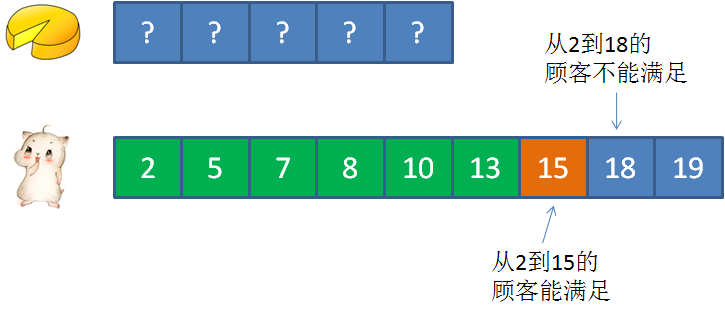
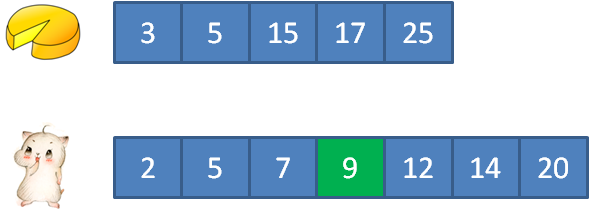
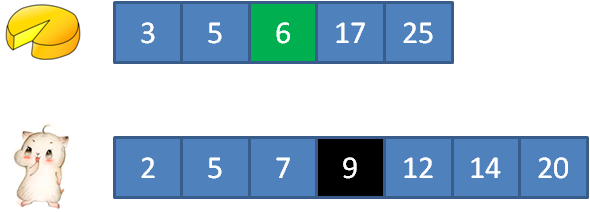
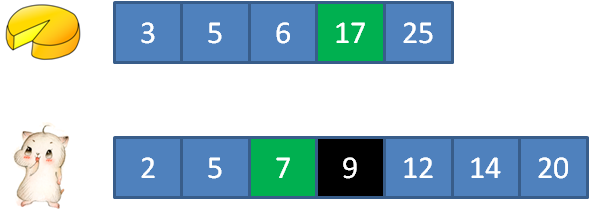
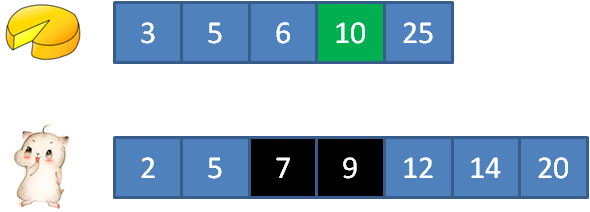
比如:输入cakes集合 {2,9};输入mouths集合 {5,4, 2,8} 正确返回:3




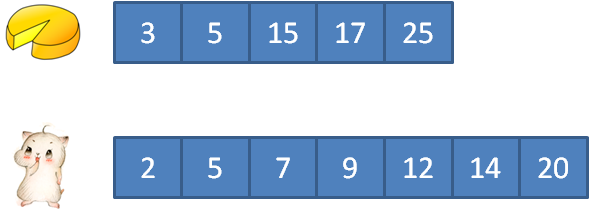

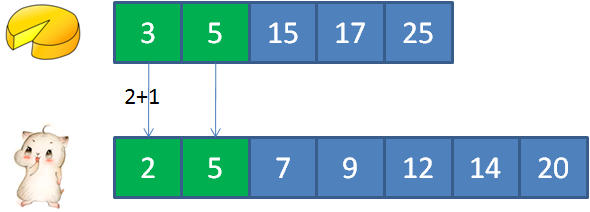
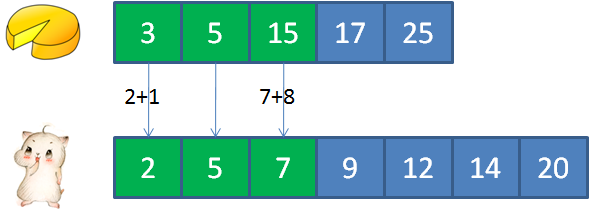
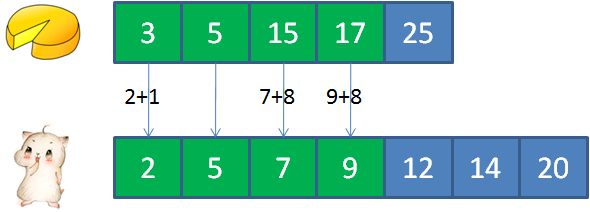
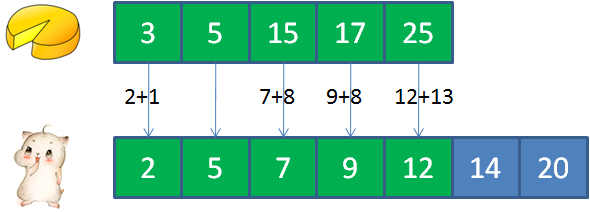

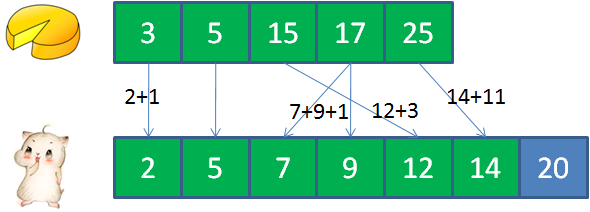
3的蛋糕满足2的顾客, 5的蛋糕满足5的顾客, 15的蛋糕满足12的顾客, 17的蛋糕满足7和9的顾客, 25的蛋糕满足14的顾客。













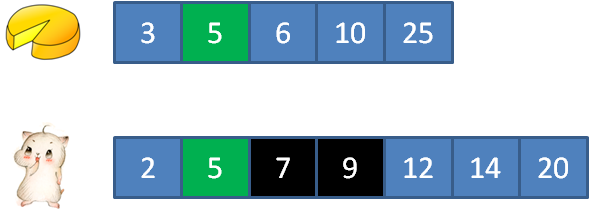
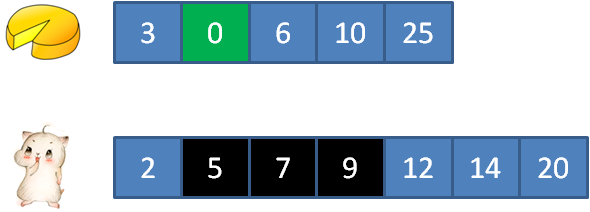
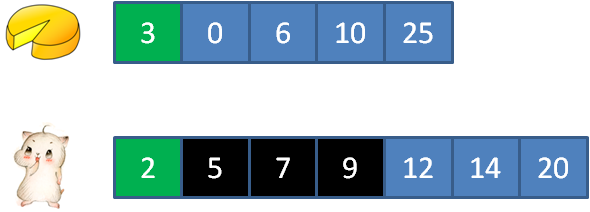
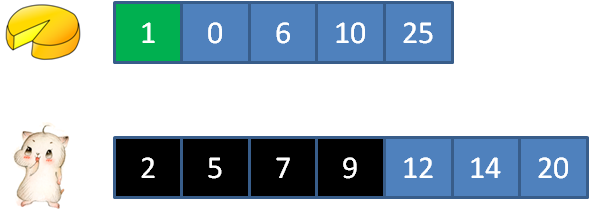
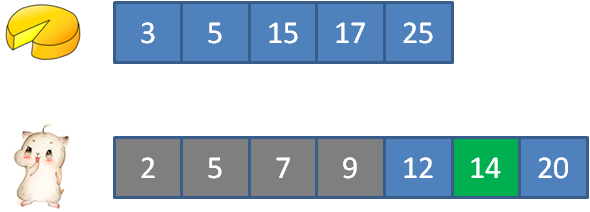
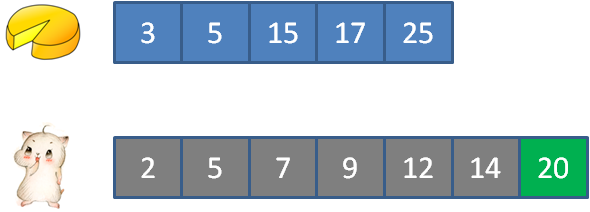


//剩余蛋糕数量
static int leftCakes[];
//蛋糕总量(不是数量,而是大小之和)
static int totalCake = 0;
//浪费蛋糕量
static int lostCake = 0;
static boolean canFeed(int[] mouths, int monthIndex, int sum)
{
if(monthIndex<=0) {
//递归边界
return true;
}
//如果 蛋糕总量-浪费蛋糕量 小于当前的需求量,直接返回false,即无法满足
if(totalCake - lostCake < sum) {
return false;
}
//从小到大遍历蛋糕
for(int i=0;i<leftCakes.length; i++) {
if (leftCakes[i] >= mouths[monthIndex]) {
//找到并吃掉匹配的蛋糕
leftCakes[i] -= mouths[monthIndex];
//剩余蛋糕小于最小的需求,变为浪费蛋糕
if (leftCakes[i] < mouths[1]){
lostCake += leftCakes[i];
}
//继续递归,试图满足mid下标之前的需求
if (canFeed(mouths, monthIndex-1, sum)) {
return true;
}
//无法满足需求,蛋糕状态回滚
if (leftCakes[i] < mouths[1]) {
lostCake -= leftCakes[i];
}
leftCakes[i] += mouths[monthIndex];
}
}
return false;
}
public static int findMaxFeed(int[] cakes, int[] mouths){
//蛋糕升序排列,并把0下标空出
int[] cakesTemp = Arrays.copyOf(cakes, cakes.length+1);
Arrays.sort(cakesTemp);
for(int cake: cakesTemp){
totalCake += cake;
}
//顾客胃口升序排列,并把0下标空出
int[] mouthsTemp = Arrays.copyOf(mouths, mouths.length+1);
Arrays.sort(mouthsTemp);
leftCakes = new int[cakes.length+1];
//需求之和(下标0的元素是0个人的需求之和,下标1的元素是第1个人的需求之和,下标2的元素是第1,2个人的需求之和.....)
int[] sum = new int[mouths.length+1];
for(int i=1;i<=mouths.length;i++) {
sum[i] = sum[i - 1] + mouthsTemp[i];
}
//left和right用于计算二分查找的“中点”
int left=1,right=mouths.length;
//如果胃口总量大于蛋糕总量,right指针左移
while(sum[right]> totalCake){
right--;
}
//中位指针,用于做二分查找
int mid=((left+right)>>1);
while(left<=right)
{
//重置剩余蛋糕数组
leftCakes = Arrays.copyOf(cakesTemp, cakesTemp.length);
//重置浪费蛋糕量
lostCake =0;
//递归寻找满足需求的临界点
if(canFeed(mouthsTemp, mid, sum[mid])){
left=mid+1;
} else {
right = mid - 1;
}
mid=((left+right)>>1);
}
//最终找到的是刚好满足的临界点
return mid;
}
public static void main(String[] args) {
int[] cakes = new int[]{3,5,15,17,25};
int[] mouths = new int[]{2,5,7,9,12,14,20};
int maxFeed = findMaxFeed(cakes, mouths);
System.out.println("最大满足顾客数:" + maxFeed);
}
主流程方法findMaxFeed,执行各种初始化,控制二分查找流程。 方法canFeed,用于检验某一位置之前的顾客是否能被给定蛋糕满足。 数组leftCakes,用于临时存储剩余的蛋糕大小,每次重新设置中间下标时,这个数组需要被重置。





延伸阅读👇

延伸阅读《算法导论》
评论
