迭代(iteration)和递归(recursion)
一、
Q.请写一段代码来计算给定文本(AAA rating)内字符“A”的个数。分别用迭代和递归两种方式。
A.
迭代方式的代码如下:
public class Iteration {
public int countA(String input) {
if (input == null || input.length( ) == 0) {
return 0;
}
int count = 0;
for (int i = 0; i < input.length( ); i++) {
if(input.substring(i, i+1).equals("A")){
count++;
}
}
return count;
}
public static void main(String[ ] args) {
System.out.println(new Iteration( ).countA("AAA rating")); // Ans.3
}
}
递归方式的代码如下:
public class RecursiveCall {
public int countA(String input) {
// exit condition – recursive calls must have an exit condition
if (input == null || input.length( ) == 0) {
return 0;
}
int count = 0;
//check first character of the input
if (input.substring(0, 1).equals("A")) {
count = 1;
}
//recursive call to evaluate rest of the input
//(i.e. 2nd character onwards)
return count + countA(input.substring(1));
}
public static void main(String[ ] args) {
System.out.println(new RecursiveCall( ).countA("AAA rating")); // Ans. 3
}
}
Q.什么情况下应该采用递归?
A. 上面的例子中其实不必采用递归,循环的方式可以达到目的,但是在某些情况下采用递归方式则代码会更加简短易读。递归方法在循环树结构以及避免丑陋的嵌套循环的情况下是非常好用的。
Q.尾递归的好处是什么?上面的代码用尾递归方式如何重写?
A.
常规递归方法(亦称,头递归)在上面演示了,这种方式会增加调用栈的大小。每次递归,其入口需要被记录在栈中。方法返回之前需要给countA(input.substring(1)的结果加一个count。假定count大于1,那么返回结果就是count + countA(input.substring(1)),当然事先要算出来countA(input.substring(1))才行。同时,这也意味着直到countA(input.substring(1)计算出来才能得到最终的结果。因此,最后需要做的事其实是加法运算,而非递归本身。
在尾递归中,最后要做的是递归,加法运算在之前就已经完成了。一轮递归调用完毕后就没有其他事情了(除了加法运算),因此调用时生成的信息也就没什么用了。这些无用信息可以丢弃,然后用一组新的参数来调用一次递归方法来产生一个新的结果。这也就是说,栈调用减少带来了内存消耗减少并且程序的性能更好。
尾递归代码重写如下:
public class TailRecursiveCall {
public int countA(String input) {
// exit condition – recursive calls must have an exit condition
if (input == null || input.length() == 0) {
return 0;
}
return countA(input, 0) ;
}
public int countA(String input, int count) {
if (input.length() == 0) {
return count;
}
// check first character of the input
if (input.substring(0, 1).equals("A")) {
count = count + 1;
}
// recursive call is the last call as the count is cumulative
return countA(input.substring(1), count);
}
public static void main(String[] args) {
System.out.println(new TailRecursiveCall().countA("AAA rating"));
}
}
二、几个经典递归案例
Q.斐波那契数列
A.斐波那契数列的排列是:0,1,1,2,3,5,8,13,21,34,55,89,144……依次类推下去,你会发现,它后一个数等于前面两个数的和。在这个数列中的数字,就被称为斐波那契数。
递归思想:一个数等于前两个数的和。
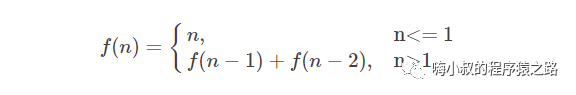
/**
* 斐波那契数列的递归写法 核心:一个小的解决终点,然后大的问题可以循环在小问题上解决
*
* @param n
* @return
*/
private static long F(int n) {
if (n <= 1)
return n;
return F(n - 1) + F(n - 2);
}
/**
* 斐波那契数列的递推写法
*
* @param n
* @return
*/
private static long F1(int n) {
if (n <= 1)
return n;
long fn = 0;
long fn_1 = 1;
long fn_2 = 0;
for (int i = 2; i <= n; i++) {
fn = fn_1 + fn_2;
fn_2 = fn_1;
fn_1 = fn;
}
return fn;
}
public static void main(String[ ] args) {
System.out.println(F(10)); // Ans. 55
System.out.println(F1(10)); // Ans. 55
}
可以看到,递归写法简单优美,省去考虑很多边界条件的时间。当然,递归算法会保存很多的临时数据,类似于堆栈的过程,如果栈深太深,就会造成内存用尽,程序崩溃的现象。Java为每个线程分配了栈大小,如果栈大小溢出,就会报错,这时候还是选择递推好一点。
Q. 阶乘(例如5的阶乘:5*4*3*2*1=120)
A.递归思想:n! = n * (n-1)!
代码如下:
private static long factorial(int n){
if (n <=1) return 1;
return factorial(n-1)*n;
}
Q.倒序输出一个正整数(例如n=12345,希望逆序输出54321)
A.
递归思想:首先输出这个数的个位数,然后再输出前面数字的个位数,直到之前没数字。
/**
* 倒序输出正整数的各位数
* @param n
*/
private static void printDigit(int n){
System.out.print(n%10);
if (n > 10){
printDigit(n/10);
}
}
Q.汉诺塔
A.数学描述就是:
有三根杆子X,Y,Z。X杆上有N个(N>1)穿孔圆盘,盘的尺寸由下到上依次变小。要求按下列规则将所有圆盘移至Y杆:
1. 每次只能移动一个圆盘;
2. 大盘不能叠在小盘上面。
递归思想:
1. 将X杆上的n-1个圆盘都移到空闲的Z杆上,并且满足上面的所有条件
2. 将X杆上的第n个圆盘移到Y上
3. 剩下问题就是将Z杆上的n-1个圆盘移动到Y上了
公式描述有点麻烦,用语言描述下吧:
1. 以Y杆为中介,将前n-1个圆盘从X杆挪到Z杆上(本身就是一个n-1的汉诺塔问
题了!)
2. 将第n个圆盘移动到Y杆上
3. 以X杆为中介,将Z杆上的n-1个圆盘移到Y杆上(本身就是一个n-1的汉诺塔问题了!)
代码如下:
