图解统计学:一文轻松搞懂基础概率+描述性统计
1
描述性统计
统计性描述分析是作为统计分析的第一步,在日常的数据分析中其实我们经常使用一些特征值,尤其是我们做周报或者月报的分析时,这些描述性的统计分析特征值对于我们有一定的帮助,描述性统计分析是进行正确的统计推断的先决条件。通过数据的分布类型和特点、集中和离散程度可进行初步分析。
描述性统计有几个常用指标,分别是:平均值、四分位数、标准差、标准分。
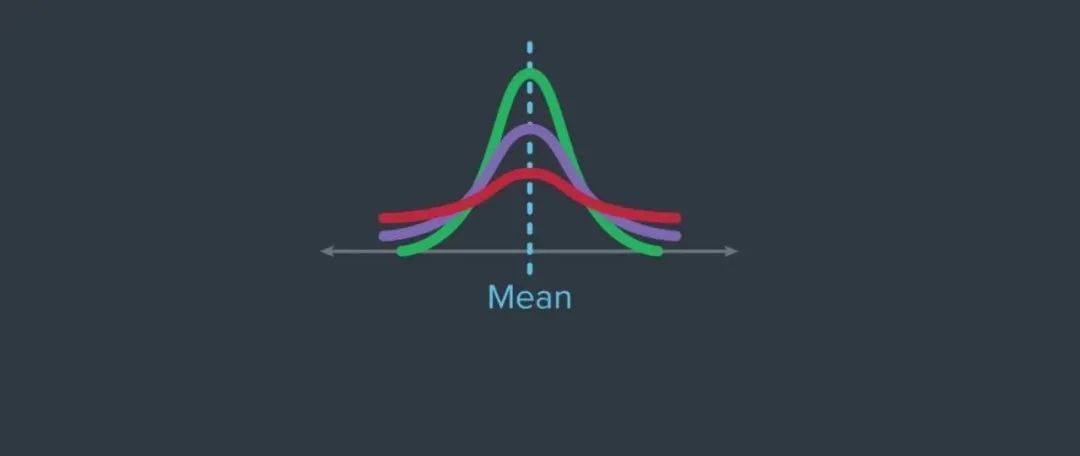
(1)平均值(μ:读“miu”),平均值是统计学最常用的统计量,是集中趋势最常用的测度值,除平均数外还有众数、中位数等集中趋势常用值。
平均数:就是一组数据之和除以这组数据的个数,缺点是对异常值不敏感。
众数:指一组数据中出现次数最多的那个数据,一组数据可以有多个众数,也可以没有众数。
中位数:将一组数据按大小顺序排列起来,形成一个数列,如果这组数据的个数为奇数,则居于数列中间位置的那个数据就是中位数,如数据个数为偶数,那么中位数就是位于中间的两个数值的平均值。
(2)四分位数:将一组数据从小到大升序排列,分成4等分,处于1/4,1/2,3/4的数值是四分位数,我们将这三个数值分别称为:下四分位数、中位数、上四分位数。

四分位数有一个非常生动的表现形式,就是箱线图,我们可以通过箱线图来比较不同类别的数据。
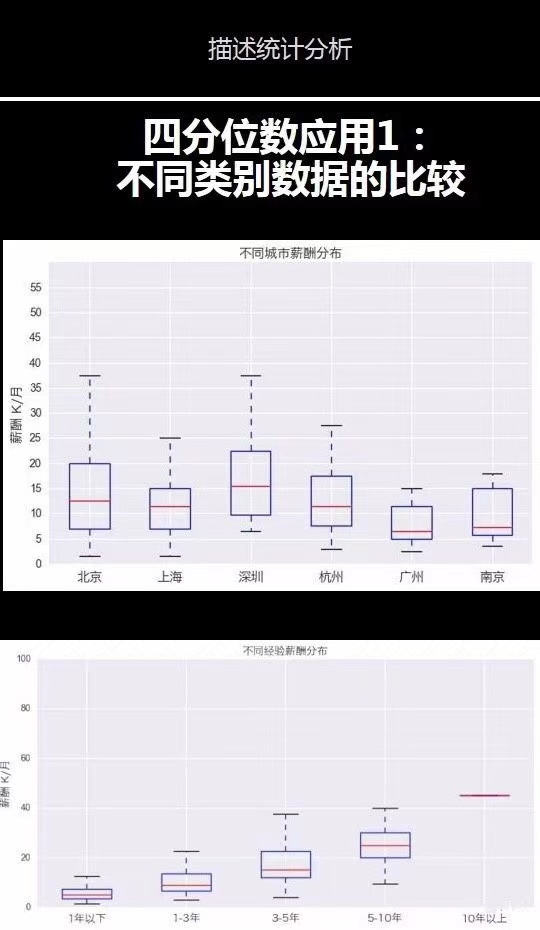
我们还可以应用四分位数通过Tukey's test方法来识别出一组数据中可能的异常值。
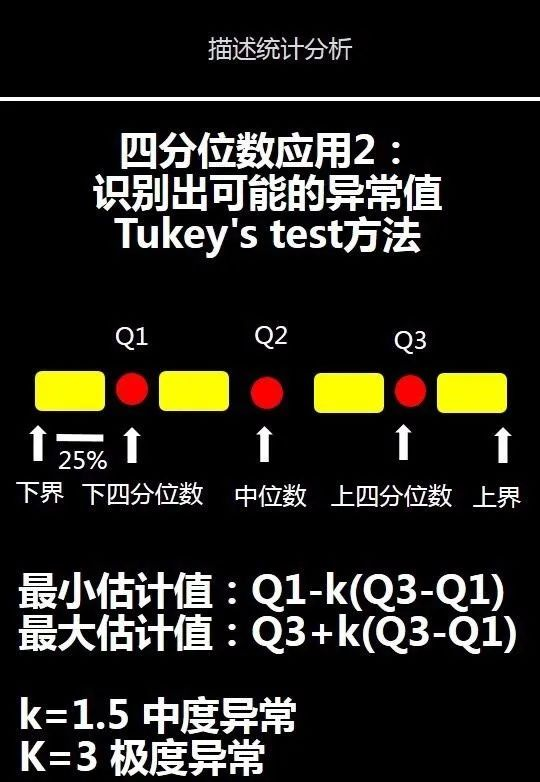
蓝色范围就是极度异常数值,红色则为中度异常数值。
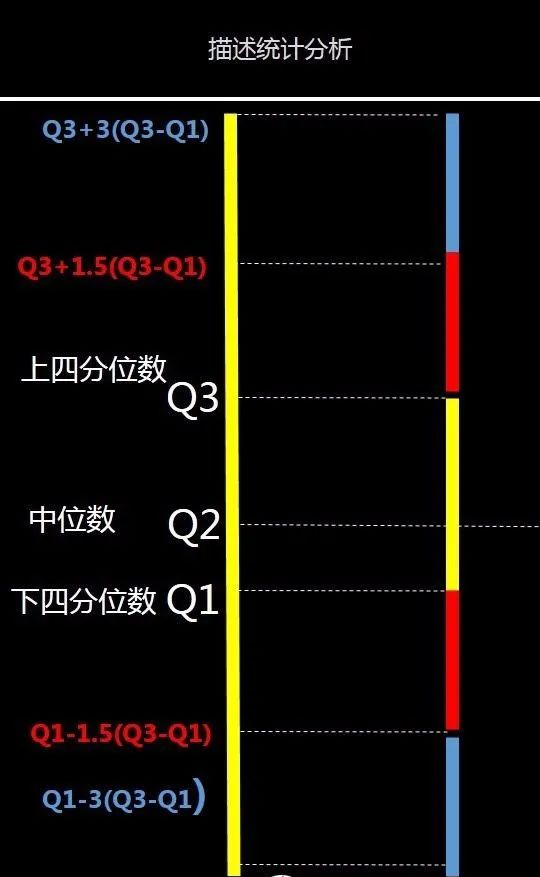
(3)标准差(读“西格玛”),方差的算术平方根,反映一组数据内个体间的离散程度(也称为波动大小)。
(4)标准分,用来表示一组数据中某个数值距离平均值多少个标准差:
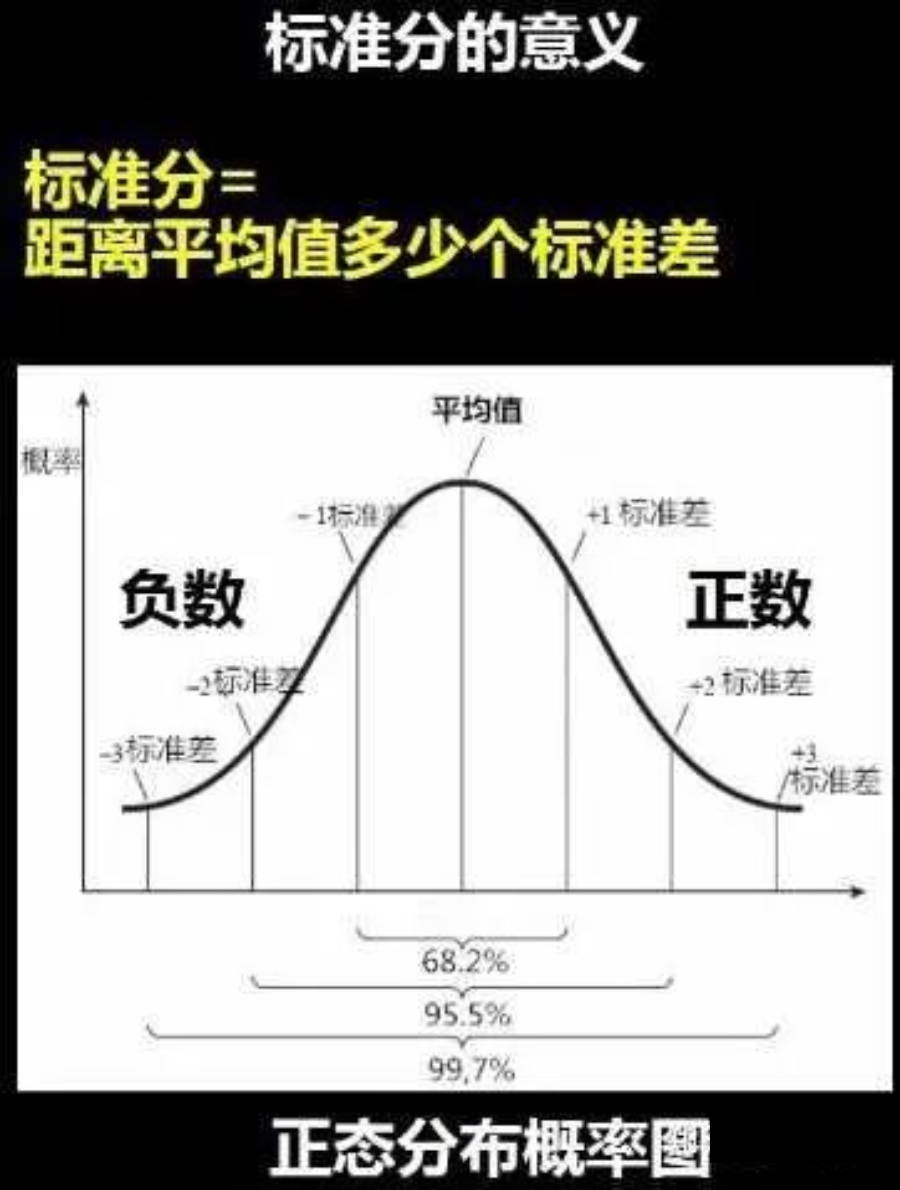
2
概率
概率,简单来说就是用数值来表示某件事发生的可能性,这个数值一定是介于0和1之间的。
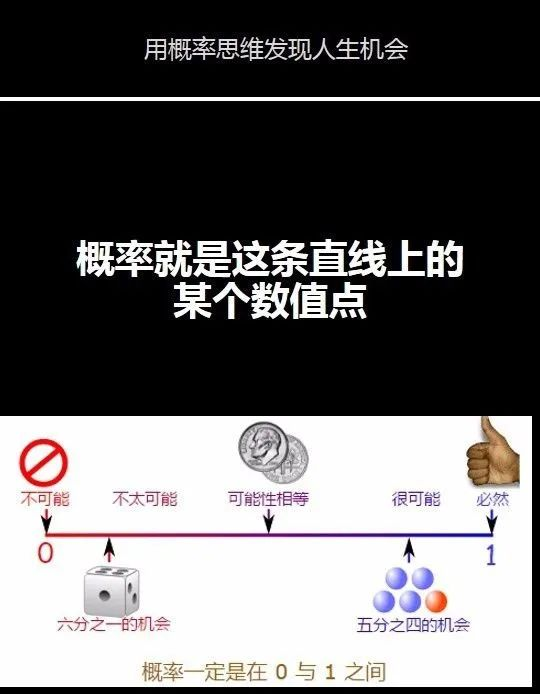
简单的概率计算可以总结为一个公式:

复杂的概率计算有两种方法:
方法一:寻找行业里权威机构发布的概率作为参考
方法二:数据分析
可以应用在生活中的几种概率思维:
赌徒谬论
赌徒谬论也称为蒙地卡罗谬论,是一种错误的信念,以为随机序列中一个事件发生的机会率与之前发生的事件有关,即其发生的机会率会随着之前没有发生该事件的次数而上升。如重复抛一个公平硬币,而连续多次抛出反面朝上,赌徒可能错误地认为,下一次抛出正面的机会会较大。
独立事件这一概念就可以详细解释为何以上观念会被称为谬论。独立事件就是事件B发生或不发生对事件A不产生影响,就说事件A与事件B之间存在某种“独立性”,其对象可以是多个。
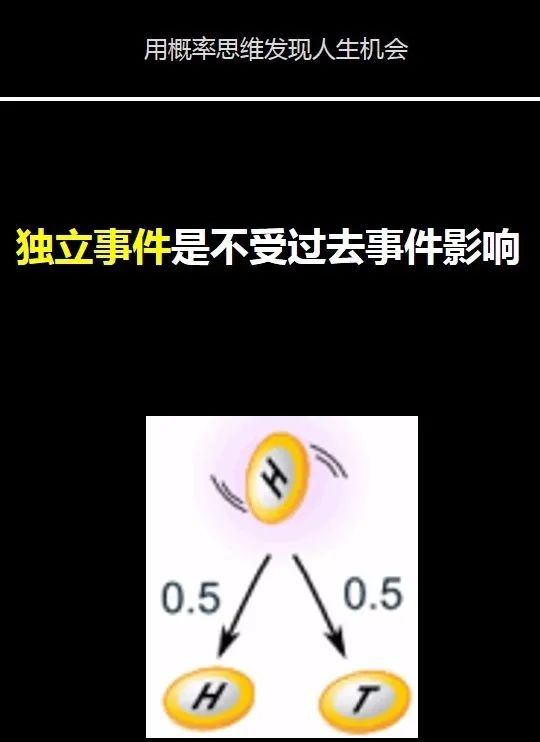
大数定律
想要理解大数定律,必须先了解什么事小数定律:


本章学习内容只是笼统的概括了跟数据分析相关的统计学基础知识,关于统计学,还有很多值得我们去探索、学习,去从中发现乐趣。了解统计学才能为我的数据分析奠定坚实的基础。路还很长,坚持下去。
END
本文为转载分享&推荐阅读,若侵权请联系后台删除